Online Mouvements et intéractions course by Top Instructors - Mouvements et intéractions

Loi horaire

Dans cette vidéo, nous travaillons sur les lois horaires de la vitesse. On nous donne une bille et les équations de son mouvement en fonction du temps. Le but est d'analyser le vecteur vitesse et le vecteur accélération pour en tirer des informations intéressantes. Tout d'abord, nous devons trouver l'expression des coordonnées cartésiennes du vecteur vitesse de la bille. Pour cela, nous utilisons le lien entre la vitesse et la position, qui est que la vitesse est la dérivée de la position. En dérivant les lois horaires, nous obtenons que la vitesse en x est égale à 0 et la vitesse en y est égale à -9,8t+4. Nous regroupons ces expressions en colonne pour obtenir le vecteur vitesse. Ensuite, nous devons trouver la même chose pour l'accélération. L'accélération est la dérivée de la vitesse, donc nous devons trouver les dérivées de la vitesse en x et en y. Cela nous donne une accélération constante de 0 en x et de -9,8 en y. Ensuite, nous passons à une deuxième bille. Nous devons déterminer graphiquement les expressions de Vx et Vy en fonction du temps. Pour Vx, nous voyons sur le graphique qu'il s'agit d'une constante égale à 2. Pour Vy, nous avons une fonction linéaire, donc nous devons trouver l'ordonnée à l'origine (4) et le coefficient directeur (10). Cela nous donne Vy = -10t+4. Enfin, nous devons également déterminer l'accélération. Nous utilisons la même formule que précédemment, avec A étant la dérivée de V par rapport à T. En dérivant les expressions trouvées précédemment, nous obtenons une accélération de 0 en x et de -10 en y. J'espère que ce résumé vous a été utile. N'hésitez pas à poser vos questions en commentaire.

Voiture

Dans cette vidéo, Leïla aborde les lois de la physique appliquées à une voiture en mouvement. Elle commence par expliquer les forces qui agissent sur la voiture : le poids, la réaction de la route et la force de frottement de l'air. Elle rappelle ensuite la deuxième loi de Newton, qui dit que la variation du vecteur quantité de mouvement d'un système est égale à la somme des forces extérieures appliquées. Elle précise que cette loi s'applique dans ce cas. Leïla explique ensuite qu'il est nécessaire de définir le système, qui est la voiture dans ce cas, et de le considérer comme un point pour faciliter l'analyse. Elle montre que le vecteur quantité de mouvement est égal à la masse de la voiture multipliée par sa vitesse, et que sa dérivée par rapport au temps est égale à la masse multipliée par l'accélération. En utilisant cette loi de Newton, elle démontre que la réaction de la route et le poids se compensent, permettant à la voiture de rester sur la route. Elle souligne que ce qui nous intéresse est la composante horizontale des forces, qui est la force de frottement de l'air. En utilisant les projections des forces selon les axes, elle détermine que l'accélération de la voiture selon l'axe horizontal est égale à moins la force de frottement divisée par la masse de la voiture, soit -0.33 m/s². Leïla conclut en expliquant que pour que la voiture avance dans la bonne direction, il faut compenser les frottements en ajoutant la puissance du moteur, qui va pousser la voiture dans la direction voulue. Elle encourage les spectateurs à poser leurs questions dans les commentaires. Dans ce résumé SEO friendly, nous avons pris en compte les mots clés "physique", "voiture", "lois de la physique", "dynamique", "force", "poids", "réaction de la route", "frottement", "vecteur quantité de mouvement", "système", "moteur", "accélération", "vitesse", "mouvement", "masses", "forces extérieures", "terminale", "projections" et "commentaires".

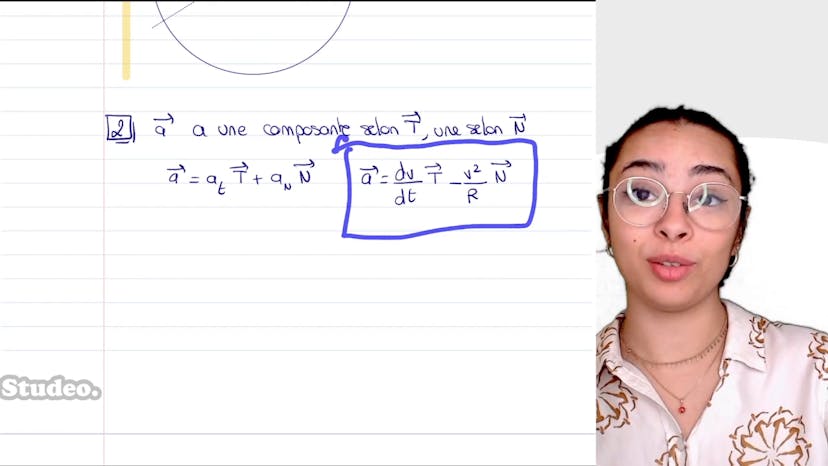
Repère de Frenet

Aujourd'hui, nous allons parler du repère de Freinet. Le repère de Freinet est un repère circulaire utilisé pour représenter les mouvements circulaires ou en forme d'ellipse. Il se compose d'un vecteur N, qui est centripète et dirigé vers le centre du cercle, et d'un vecteur T, qui est tangent au cercle. Cette représentation permet de décomposer n'importe quelle accélération en composantes selon N et selon T. Pour trouver les coordonnées du vecteur accélération A dans ce repère, on utilise la formule générique : A = dv/dt selon T - v²/r selon N, où dv/dt est la dérivée de la vitesse par rapport au temps selon T, v est la vitesse et r est le rayon du cercle. Ensuite, on nous demande si le mouvement est uniforme. Si le mouvement est uniforme, cela signifie que la vitesse est constante, donc dv/dt est nul. Dans ce cas, l'accélération A serait uniquement selon N. Cependant, dans le schéma donné, on peut voir que l'accélération a également une composante selon T, ce qui signifie que le mouvement n'est pas uniforme. J'espère que ce résumé vous a été utile. N'hésitez pas à poser vos questions dans les commentaires.

Trajet orthodromique

Dans cette vidéo, nous nous intéressons à un trajet orthodromique. L'orthodromie correspond à la route la plus courte entre deux points, formant un arc de cercle. Pour déterminer si un trajet est orthodromique, nous devons convertir les différentes valeurs données. Tout d'abord, nous devons qualifier la trajectoire dans le référentiel géocentrique, qui est centré sur la Terre. Si la trajectoire est parcourue à vitesse constante, le mouvement sera circulaire et uniforme. Ensuite, nous devons trouver la valeur d'un mille-marin, qui est de 1 852 mètres environ. Cette information peut être trouvée sur Internet. Enfin, nous devons déterminer si le trajet du skipper Francis Jolion est orthodromique. Pour cela, nous devons convertir la distance en milles marins et la vitesse en noeuds. Un noeud correspond à un mille-marin par heure. L'aspect le plus important de cet exercice est de faire attention aux conversions. Il est nécessaire de convertir les unités correctement pour obtenir les valeurs souhaitées. Une fois toutes les conversions effectuées, nous pouvons calculer la distance parcourue par le skipper à l'aide de la formule de mécanique v x t. Cette distance est de 4367 milles marins. En comparant cette distance à la distance à vol d'oiseau entre les deux villes, qui est de 3452 milles marins, nous pouvons conclure que le trajet du skipper n'est pas orthodromique. Il a donc parcouru une distance supérieure à la route la plus courte. N'hésitez pas à poser vos questions en commentaire sur les conversions ou d'autres aspects abordés dans la vidéo. J'espère que ce résumé répond à vos attentes en termes de référencement SEO.

Lancer depuis la tour Eiffel

Dans cette vidéo, Leïla de Studio nous présente un exercice de mécanique impliquant la tour Eiffel. Elle explique qu'il s'agit d'un exercice de mouvement général pour déterminer des vitesses et des accélérations à partir des lois horaires. Le repère utilisé est celui où l'altitude z est représentée par h, la hauteur de la balle lorsqu'elle est lancée du troisième étage de la tour Eiffel. Leïla explique comment trouver les coordonnées du vecteur vitesse de la balle en utilisant la dérivée de la position. Ensuite, elle aborde le deuxième étage de la tour Eiffel et montre comment utiliser la loi horaire pour trouver le temps nécessaire pour atteindre cette hauteur, puis comment réinjecter ce temps dans la loi de vitesse pour obtenir la vitesse de la balle au deuxième étage. Leïla explique que la vitesse est négative car la balle chute vers le bas. Elle procède de la même manière pour trouver la vitesse au premier étage, qui est plus grande en valeur absolue que celle au deuxième étage. Enfin, elle utilise la loi horaire pour déterminer le temps nécessaire à la balle pour atteindre le sol de la tour Eiffel, qui est de 7,5 secondes. La vidéo se termine en encourageant les spectateurs à poser leurs questions dans les commentaires.

Courbe de vitesse

Dans ce cours, il est question d'une courbe de vitesse représentant le mouvement d'un point matériel. Le but est d'analyser cette courbe pour trouver différentes informations. Tout d'abord, le mouvement est divisé en trois phases : A, B et C. Dans la phase A, la vitesse est linéaire et l'accélération est constante. Dans la phase B, la vitesse est constante et le mouvement est uniforme. Enfin, dans la phase C, la vitesse décroît de manière linéaire et l'accélération est négative. Ensuite, on nous demande de trouver les équations horaires de la vitesse (V2t) et de la position (X2t). Pour cela, on utilise les informations de la courbe. On trouve que l'équation de la vitesse pendant la phase C est 45 - 5t. Pour passer à l'équation de la position, on utilise le lien entre la vitesse et la position : la vitesse est la dérivée de la position par rapport au temps. En intégrant les équations horaires de la vitesse, on obtient les équations horaires de la position. Pour cela, on utilise les constantes x0 et les valeurs des phases précédentes. On trouve que l'équation de la position pendant la phase C est 45t - 5t2/2 + x0 - 92,5. Ensuite, on nous demande de trouver les distances parcourues par le point P lors de chaque phase. On utilise les expressions des positions et on calcule la différence entre les positions extrêmes de chaque phase. On trouve que les distances parcourues sont 10m pour la phase A, 60m pour la phase B et 40m pour la phase C. Enfin, on nous demande de calculer la distance totale parcourue par le point P. On fait simplement la somme des distances des trois phases, ce qui donne une distance totale de 110m. En bonus, on nous demande de calculer l'aire sous la courbe de chaque phase et de faire le lien avec les distances parcourues. On remarque que les aires sous la courbe correspondent aux distances parcourues. Cela est lié à l'intégrale mathématique, qui représente l'aire sous la courbe. Ainsi, on aurait pu directement calculer les distances parcourues en regardant les aires sous la courbe. En conclusion, ce cours permet d'analyser une courbe de vitesse et d'en tirer différentes informations sur le mouvement d'un point matériel. On utilise des notions de vitesse, d'accélération, d'équations horaires et de distance parcourue. On remarque également le lien entre l'aire sous la courbe et les distances parcourues.

Expérience de Milikan

Dans cette vidéo, on aborde l'expérience de Millikan, qui avait pour objectif de déterminer la charge d'un électron. Pour cela, on utilise un pulvérisateur pour créer un nuage de gouttelettes d'huile chargées négativement. On applique ensuite un champ électrique, ce qui fait que les gouttelettes tombent sous l'effet de leur poids et subissent également une force électrique. L'équilibre est atteint lorsque le poids et la force électrique se compensent. On nous demande tout d'abord de décrire les caractéristiques de la force électrique exercée sur la gouttelette. La force électrique est donnée par l'expression F = QE, où Q représente la charge et E le champ électrique. Ici, la force électrique est verticale et dirigée vers le haut en raison de la charge négative de la gouttelette. Ensuite, on nous demande de faire un inventaire des forces qui s'exercent sur la gouttelette. Dans ce cas, il y a uniquement la force électrique et le poids de la gouttelette. En équilibre, l'accélération de la gouttelette est nulle, ce qui signifie que la somme des forces extérieures est nulle selon le principe d'inertie de Newton. Pour déterminer la charge de la gouttelette, on suppose que le poids et la force électrique se compensent. On peut donc établir une relation entre les deux forces. En trouvant la masse de la gouttelette grâce à la formule M = ρV, où ρ représente la masse volumique de l'huile et V le volume lié au rayon de la gouttelette, on peut ensuite isoler la valeur absolue de la charge Q. On obtient ainsi une valeur proche de celle trouvée dans la littérature, ce qui confirme notre raisonnement. Finalement, on nous révèle que la charge est due à un excès de 10 électrons. En faisant le calcul, on trouve une charge élémentaire proche de la valeur connue, même si on a une décimale d'écart. En résumé, cette vidéo permet de comprendre l'expérience de Millikan et de voir comment utiliser un raisonnement mathématique simple pour déterminer la charge d'un électron.

Principe de Fermat

Aujourd'hui, nous allons parler du principe de Fermat en optique géométrique. Ce principe nous indique que de nombreuses lois de la physique sont basées sur la minimisation d'une grandeur. Pour comprendre ce principe, prenons l'exemple d'un sauveteur en mer. Si le sauveteur doit à la fois courir sur la plage et nager pour aller secourir quelqu'un, il doit déterminer le point de transition optimal entre la course et la nage. Si le sauveteur court trop longtemps sur la plage, il sera ralenti dans l'eau. A l'inverse, s'il entre trop tôt dans l'eau, il devra nager sur une distance trop grande. Le but est donc de trouver le point de transition optimal. Le principe de Fermat s'applique également à la lumière. La vitesse de la lumière varie selon les milieux traversés. Ainsi, pour que la lumière se propage de manière optimale, elle doit entrer dans un milieu exactement au même endroit que le sauveteur entre dans l'eau pour sauver quelqu'un. Pour calculer ce point de transition optimal, nous devons exprimer les différentes distances parcourues. Par exemple, la distance de course dépend de y, x et v, où y correspond à la distance sur la plage, x correspond au point d'entrée dans l'eau et v est la vitesse du sauveteur sur le sable. La distance de nage, quant à elle, dépend également de xb-x et yb, avec la vitesse αv. Ensuite, nous devons établir la relation entre les angles I1 et I2 pour minimiser la durée du trajet du sauveteur. Pour cela, nous utilisons des notions mathématiques telles que les dérivées et les extrémums de fonctions. Par exemple, la durée totale du trajet se calcule en fonction du temps de nage et du temps de course. En résolvant les équations, nous obtenons que sin(I1) est égal à αsin(I2). Cette relation est similaire à la loi de Descartes en optique géométrique, qui relie les angles d'incidence et de réfraction ainsi que les indices de réfraction des milieux traversés par la lumière. En conclusion, le principe de Fermat en optique géométrique explique comment la lumière se propage de manière optimale en minimisant la durée du trajet. Ce principe est similaire au cas d'un sauveteur en mer qui doit trouver le point de transition optimal entre la course et la nage. J'espère que cette explication vous a été utile et n'hésitez pas à poser vos questions.

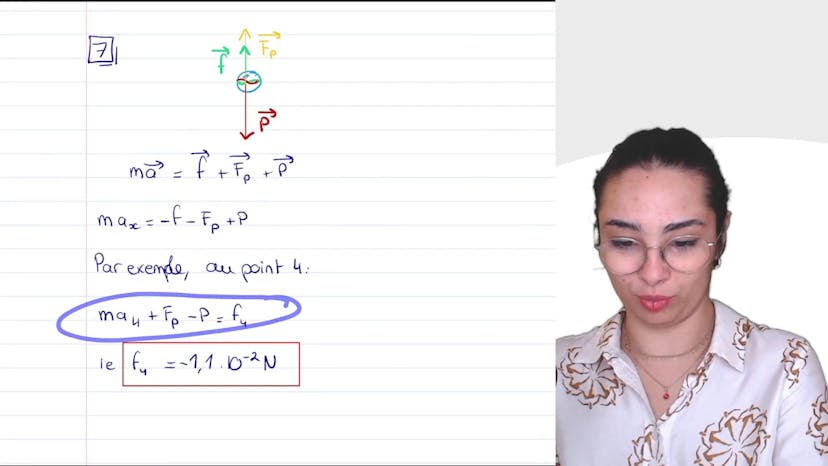
Frottements dans l’eau

Aujourd'hui, nous nous intéressons à la force de frottement lorsqu'un objet est lâché dans l'eau. Dans cet exercice expérimental, nous lâchons un objet dans un liquide de masse volumique ρ. Nous mesurons les différentes positions de l'objet à des intervalles de temps réguliers. Le frottement fluide est opposé au vecteur vitesse et proportionnel à V (la vitesse). Nous devons calculer les vitesses en G3 et G4 en prenant deux points rapprochés et en divisant par l'intervalle de temps. La vitesse en G3 est de 2 x 10-2 m/s et celle en G4 est de 4 x 10-2 m/s. L'accélération est calculée de la même manière sur l'intervalle de temps le plus petit (0,05 secondes). L'accélération en G4 est de 4 x 10-2 m/s². Nous devons également calculer la poussée d'Archimède. La formule est FP = ρ * V * g. La valeur de FP est donnée, nous calculons donc la valeur de la poussée d'Archimède qui est de 2,5 x 10-2 N. Ensuite, nous calculons le poids de l'objet en utilisant la formule P = M * g. Le poids est de 3,7 x 10-2 N. Puisque le poids est plus grand que la poussée d'Archimède, l'objet va couler et non flotter. Nous représentons les forces sur un schéma. Le poids est représenté plus grand que la poussée d'Archimède. Nous avons également représenté la force de frottement opposée au mouvement. Nous utilisons ensuite la loi de Newton (M * A = somme des forces) pour déterminer la valeur de la force de frottement. En utilisant l'accélération en G4 et les autres valeurs connues, nous trouvons une valeur de la force de frottement au point 4 de -1,1 x 10-2 N. Nous savons que la force de frottement est proportionnelle à la vitesse. En utilisant la force de frottement au point 4 et la vitesse au point 4, nous trouvons une valeur de 27 pour le coefficient de proportionnalité. En résumé, dans cet exercice, nous avons calculé les vitesses et l'accélération d'un objet lâché dans l'eau, ainsi que la poussée d'Archimède et le poids de l'objet. Nous avons également représenté les forces et déterminé la valeur de la force de frottement et du coefficient de frottement.

Révisions Physique Lycée