 All subjects
All subjects
 All subjects
All subjects
Prépa Examens
Concours et examens UK
Terminale

Polynôme de degré 4 et nombres premiers
Le cours aborde un exercice du Mass Admission Test Docteur sur la factorisation et les nombres entiers. Il commence par analyser l'énoncé où il est demandé de factoriser le polynôme x^4 + 1. Il montre ensuite la factorisation en utilisant la formule (a^2 + b^2) = (a + b)^2 - 2ab. Il explique également qu'il est possible de factoriser tous les polynômes de degré supérieur à 2. Il montre ensuite que pour tout réel n, n^4 + 4 ne peut pas être un nombre premier. Il utilise une condition nécessaire pour être premier et montre qu'elle est vérifiée pour n=1, mais pas pour d'autres valeurs de n. Finalement, il conclut que l'ensemble des solutions de l'équation est réduit à l'entier 1.
Prépa Examens
Concours et examens UK
Terminale

100 cercles concentriques !
Dans cette vidéo, l'exercice de géométrie du mathématicien test d'Oxford et Imperial de l'édition 2022 est abordé. L'exercice présente une centaine de cercles concentriques, nommés C1, C2, C3, jusqu'à C100. Pour chaque nombre entier de 1 à 99 inclus, une tangente du cercle Cn est tracée et elle croise le cercle Cn+1 en deux points distants de 2. Considérant que le rayon du cercle C1 est de 1, l'objectif est de déterminer le rayon du cercle C100.
En analysant la figure, on peut constater que les rayons des cercles augmentent successivement. En traçant une tangente au cercle C1 et en observant ses points d'intersection avec le cercle C2, on peut comprendre que la distance entre ces points dépend de la taille du cercle suivant. Il faut donc trouver une méthode générale pour calculer cette distance.
En utilisant le théorème de Pythagore, on peut établir que (rn+1)^2 = 1 + (rn)^2, où rn est le rayon du cercle Cn. Cette relation est valable entre n'importe quels cercles successifs. En résolvant cette équation récursive, on peut exprimer le rayon du cercle Cn en fonction de n, ce qui donne rn = racine carrée de n.
Ainsi, en substituant n par 100, on obtient le rayon du cercle C100 qui est égal à racine carrée de 100, soit 10.
Prépa Examens
Concours et examens UK
Terminale

Équation à valeur absolue
Bienvenue à tous dans cette vidéo de correction du premier exercice de l'édition 2022 du Math Admission Test d'Oxford. Dans cet exercice, nous devons trouver le nombre de solutions réelles d'une équation donnée. Pour résoudre ce problème, il est important de bien comprendre le concept de valeur absolue. Nous devons distinguer les cas où x est positif et négatif, puis manipuler l'expression en conséquence. En utilisant cette méthode, nous pouvons résoudre l'équation en quelques étapes simples. Nous pouvons également utiliser la méthode du delta pour simplifier le calcul des racines. Dans cet exercice, nous trouvons trois racines réelles. Il est important de maîtriser ces méthodes car elles peuvent être utiles pour résoudre des problèmes similaires dans le futur. N'hésitez pas à poser des questions si nécessaire et à rejoindre notre communauté. Au plaisir de vous retrouver dans la prochaine vidéo.
Prépa Examens
Concours et examens UK
Terminale

Équation d'un cercle et degré 3 ?
Aucun résumé n'est disponible pour cette vidéo
Prépa Examens
Concours et examens UK
Terminale

Une suite hyper géométrique !
Ce cours est une transcription d'une vidéo qui explique la résolution d'une question du Math Admission Test d'Oxford 2022.
La question porte sur une suite mathématique avec une relation de récurrence. La méthode utilisée pour résoudre la question est d'appliquer le logarithme naturel (ln) pour gérer les puissances. En utilisant cette méthode, on trouve une formule qui permet de trouver les termes de la suite.
Ensuite, on applique cette formule pour trouver la valeur du dixième terme de la suite. Après quelques manipulations, on obtient la réponse finale.
Le cours souligne l'importance d'avoir de bons réflexes et une connaissance des formules mathématiques pour résoudre ce type de question. La méthode utilisée permet de résoudre la question rapidement, en quelques minutes.
L'objectif du cours est d'aider les étudiants à développer ces réflexes et à acquérir une bonne connaissance des formules mathématiques pour réussir ce type de test.
Prépa Examens
Concours et examens UK
Terminale
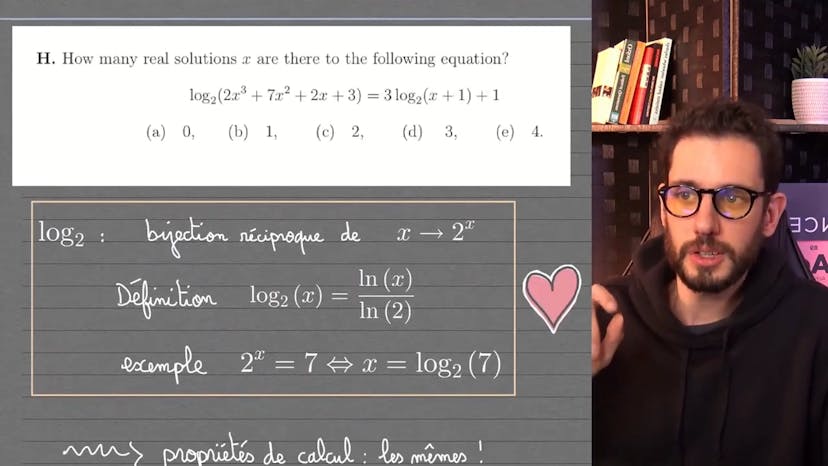
Logarithme en base 2 et résolution d'équation
Dans cette vidéo, TheMathTailor résout une équation mathématique posée au MathAdmissionTest d'Oxford en 2022.
Il commence par expliquer ce qu'est un log non classique en base 2, qui est la bijection réciproque de la fonction 2 puissance x. Il rappelle également que l'exponentiel x est égal à 2 puissance x.
Ensuite, il factorise l'équation donnée et trouve un polynôme du degré 2. Il résout ce polynôme et trouve deux solutions possibles pour x.
Cependant, il souligne qu'il faut vérifier les conditions d'existence de ces solutions. Il rappelle que le log en base 2 n'est défini que pour des valeurs strictement positives de x. Après vérification, il conclut que les deux solutions trouvées sont bien valides.
En résumé, l'équation donnée a deux solutions réelles valides.
Prépa Examens
Concours et examens UK
Terminale
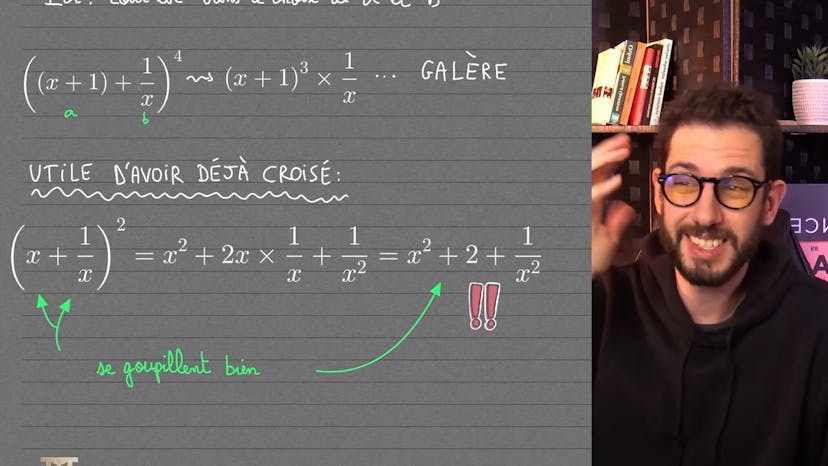
Une fonction avec du degré 4 et -4 !
Bonjour à tous et bienvenue dans cette vidéo. Aujourd'hui, nous allons analyser un exercice du Math Admission Test qui consiste à trouver le nombre de termes constants dans une expression donnée.
Tout d'abord, rappelons les règles de développement des puissances supérieures à 2. Pour une puissance 2, nous avons a^2 + b^2. Pour les puissances supérieures, il existe des identités remarquables, mais nous pouvons également utiliser le triangle de Pascal. En combinant les puissances de chaque terme et les coefficients du triangle de Pascal, nous obtenons le développement de l'expression.
Maintenant, concentrons-nous sur l'exercice. Pour simplifier les calculs, nous allons choisir a = x + 1/x et b = 1. Cette combinaison nous permet de facilement combiner les termes en x et en 1/x. En utilisant le développement 1, 4, 6, 4, 1 du triangle de Pascal, nous obtenons l'expression développée.
Nous remarquons que les termes impairs ne seront pas utiles pour trouver les termes constants. Seuls les termes pairs où les puissances de x et de 1/x se compensent seront importants. En effectuant quelques calculs, nous trouvons le terme constant de l'expression.
En résumé, en utilisant le triangle de Pascal et en choisissant judicieusement les valeurs de a et b, nous pouvons rapidement trouver les termes constants dans une expression. J'espère que cette méthode vous a été utile. Merci de m'avoir suivi et à bientôt !
Prépa Examens
Concours et examens UK
Terminale
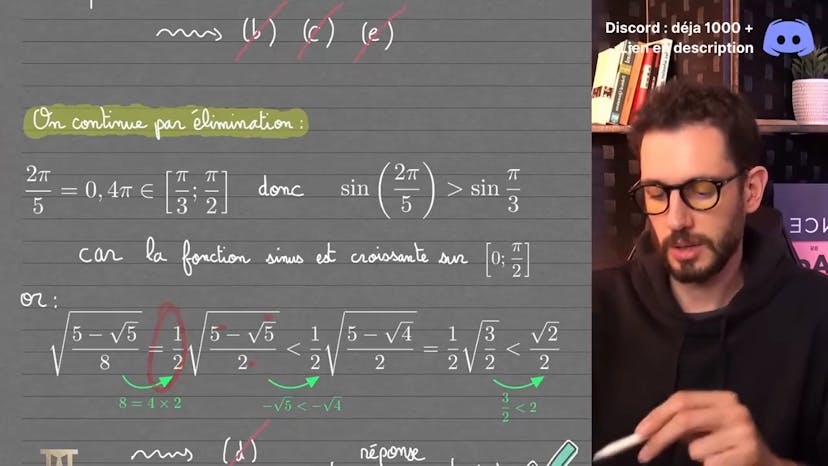
De la trigonométrie !
Ce cours est une transcription d'une vidéo qui explique une question de trigonométrie du Math Admission Test d'Oxford 2022. La question donne une relation sin5θ = 5sinθ - 20sinθ^3 + 16sinθ^5 et demande la valeur de sin72°. Le professeur utilise une méthode d'élimination pour trouver la réponse en commençant par éliminer les réponses qui donnent des valeurs négatives dans le quadrant où sin72° se trouve. Ensuite, il utilise la connaissance que sin72° est équivalent à 2π/5 pour éliminer les autres réponses et trouve que la réponse correcte est A. Il explique également une méthode plus longue qui utilise des équations polynomiales pour trouver la réponse, mais qui prend plus de temps. Il conseille de rester concentré sur les informations données dans la question et de ne pas s'égarer sur des méthodes plus complexes.


