Online Oxford Imperial MAT course by Top Instructors - Oxford Imperial MAT

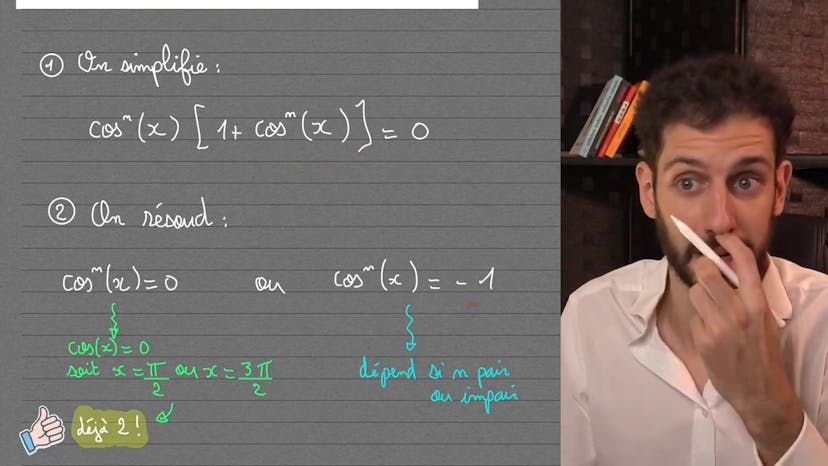
cosⁿ(x) et du sinⁿ(x) dans une équation ?

Le cours traite de la résolution d'une équation et de la trigonométrie. L'exercice consiste à déterminer le nombre de solutions d'une équation donnée. On factorise l'équation et on obtient deux termes possibles : cosinus puissance n de x = 0 et 1 + cosinus puissance n de x = 0. On résout ces équations en fonction des valeurs de n. Pour cosinus puissance n de x = 0, on obtient deux solutions : pi/2 et 3pi/2. Pour 1 + cosinus puissance n de x = 0, on détermine si cela peut être égal à -1 en fonction de la parité de n. Si n est pair, cela n'est pas possible, donc on ne retient pas ces solutions. Si n est impair, cela est possible et on obtient une solution : x = pi. Donc, si n est impair, il y a trois solutions, sinon il y en a deux. Ainsi, on démontre que la réponse est D ou E. Cette stratégie permet de gagner du temps lors de l'examen.

Produit (et non somme) des termes d'une suite géométrique

Dans cette transcription d'une vidéo, l'auteur explique un exercice de mathématiques issu du Math Admission Test d'Oxford en 2016. Il s'agit de trouver le produit des 15 premiers termes d'une suite géométrique. L'auteur explique la méthode pour trouver la formule générale de cette suite et ensuite il calcule le produit en utilisant une formule connue des suites arithmétiques. La réponse est donc l puissance 105. L'auteur avertit qu'il y a plusieurs questions de ce type dans le concours et conseille de bien maîtriser ce genre d'exercice pour réussir le concours d'entrée en faculté.

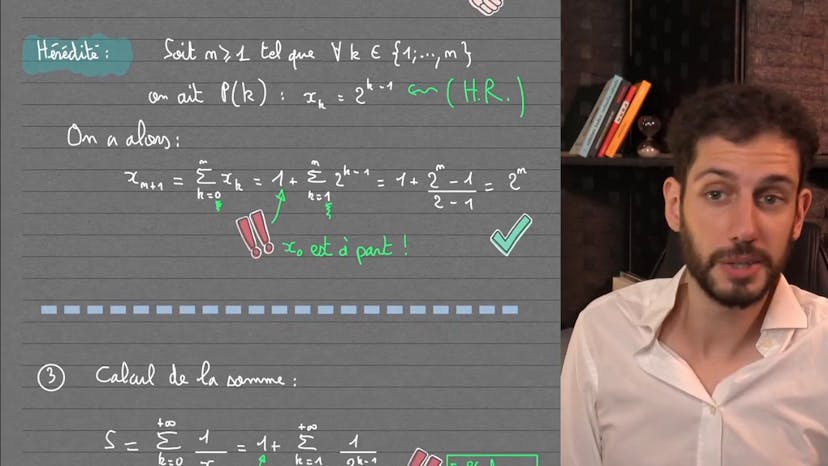
Une somme… d'inverses… de sommes !

Dans cette vidéo, l'enseignant propose de résoudre un exercice tombé à l'université d'Oxford en 2016. Il explique que même si les termes utilisés peuvent sembler complexes, il est possible de les comprendre avec de la méthode et de l'analyse. Il commence par décoder le problème et expliquer la notion d'une suite définie par des sommes successives. En calculant les premiers termes de la suite, il remarque une certaine régularité qui l'amène à formuler une hypothèse sur le calcul de xn. En utilisant la récurrence, il vérifie cette hypothèse et démontre que xn est égal à 2 puissance n moins 1. Il précise cependant qu'il faut faire attention à exclure x0 de cette formule, car elle ne s'applique qu'aux indices de 1 à n. Ensuite, il explique comment calculer la somme demandée. Il insiste sur l'importance de sortir x0 de la somme et de bien comprendre que l'expression précédente ne s'applique qu'aux indices de 1 à n. En utilisant la formule de la somme géométrique, il obtient finalement une réponse de 3. En conclusion, il souligne l'importance de bien traduire les termes de l'exercice, de comprendre les premiers termes de la suite et d'appliquer les connaissances sur x0. Il encourage les étudiants à poser des questions et se dit prêt pour la prochaine vidéo.

Une fonction trigo bien moche !

Bonjour à tous ! Dans cette vidéo, nous allons analyser une question du Math Admission Test d'Oxford en 2020. La question est la suivante : "Quelle est la plus grande valeur atteinte par l'expression 3 cos²x plus sin²x plus 1 ?". La première étape consiste à simplifier l'expression. Pour cela, nous allons utiliser une relation fondamentale de la trigonométrie qui nous dit que cos²x équivaut à 1-sin²x. En remplaçant cos²x par cette équation, nous obtenons l'expression 3-3sin²x plus 2sin²x plus 1, que nous simplifions pour obtenir 3-sin²x plus 2sin²x plus 4. Nous remarquons qu'il y a un polynôme du second degré caché dans cette expression. Pour faciliter les calculs, nous posons une variable intermédiaire grand x égale à sin²x. Nous notons également que grand x doit être compris entre -1 et 1. Ainsi, nous avons une nouvelle expression Q2x égale à -3 fois grand x² plus 2x plus 4. Nous devons déterminer la valeur maximale atteinte par cette fonction. Comme il s'agit d'un polynôme du second degré, nous savons qu'elle atteint son maximum. En utilisant la formule du maximum d'un polynôme du second degré, nous trouvons que le maximum est atteint en 1/3. Nous pouvons calculer la valeur maximale en substituant 1/3 à x dans l'expression Q. Après les calculs, nous obtenons que Q de 1/3 est égal à 13/3. Ainsi, la réponse à la question est 13/3. J'espère que ce résumé était clair et n'hésitez pas à poser des questions dans les commentaires. À bientôt pour une prochaine vidéo !

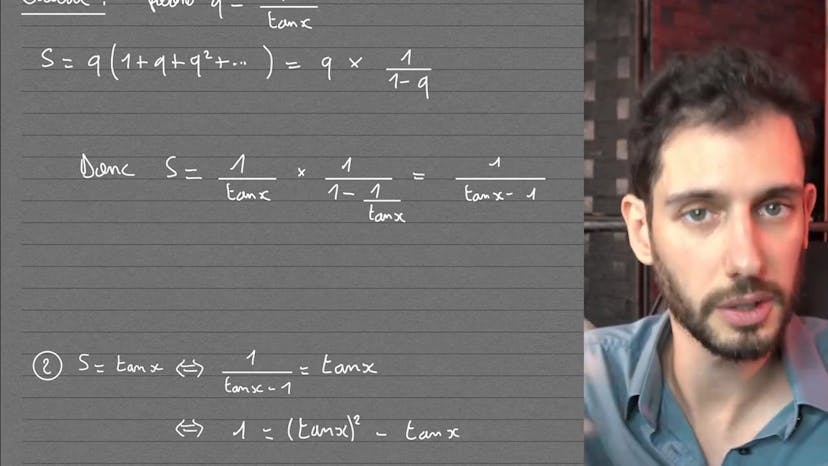
Une suite géométrique !

Bonjour à tous, je m'appelle Antonin et je suis professeur particulier de mathématiques, spécialisé dans les examens d'entrée à l'université d'Oxford. Aujourd'hui, je vais vous présenter un exercice qui est tombé à Oxford en 2020. L'énoncé demande combien de valeurs de l'angle x, situées entre -90° et 90°, permettent d'égaliser la somme infinie de 1/tangente(x) + 1/tangente^2(x), etc., à la tangente(x). Pour résoudre cet exercice, on doit tout d'abord comprendre que la fonction tangente(x) est strictement croissante entre -π/2 et π/2. On remarque également qu'on a une série de nombres élevés à des puissances croissantes. Cela nous indique qu'il s'agit d'une somme géométrique. Notre objectif est de simplifier cette somme et de trouver quand elle est égale à la tangente(x). La première étape consiste donc à simplifier la somme géométrique. Nous savons que cette somme converge si la valeur absolue de la raison (1/tangente(x)) est inférieure à 1. Ainsi, nous devons vérifier que la tangente(x) est strictement supérieure à 1 ou strictement inférieure à -1. Ensuite, nous pouvons calculer la somme géométrique en utilisant la formule Q/(1-Q), où Q est égal à 1/tangente(x). En remplaçant Q par sa valeur, nous obtenons S = 1/tangente(x) - 1. Enfin, nous devons résoudre l'équation tangente(x) = S. En posant Y = tangente(x), nous obtenons l'équation 1 = Y^2 - Y. En analysant cette équation, nous trouvons les valeurs de Y satisfaisant la condition d'équivalence. Après avoir vérifié que les solutions respectent la condition de valeur absolue supérieure à 1, nous trouvons une seule solution acceptable pour tangente(x) : 1 + racine de 5/2. En conclusion, il y a une seule valeur de l'angle x, située entre -π/2 et π/2, qui satisfait l'équation tangente(x) = 1 + racine de 5/2. J'espère que cette explication était claire et utile. Les problèmes du MIT et du Math Admissions Test d'Oxford ne sont pas simples, mais avec une bonne décomposition et l'application de ce que nous avons appris en première et en terminale, nous pouvons trouver des solutions. La réponse à cet exercice serait donc la réponse b.

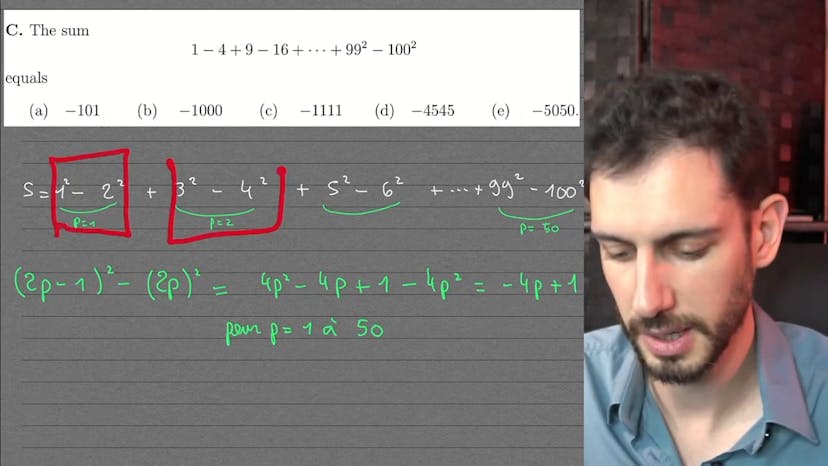
Une suite un peu bizarre

Dans cette vidéo, le professeur de mathématiques Antonin explique un exercice tombé à l'écrit d'Oxford en 2020. L'exercice consiste à analyser une somme complexe et à en trouver la généralité. Antonin explique que la clé pour résoudre cet exercice est de comprendre la structure sous-jacente des termes de la somme. Il propose de réécrire la somme en utilisant des carrés pour faciliter l'analyse. Il indique qu'il faut comprendre que les termes de la somme sont des différences entre nombres pairs et impairs. Antonin présente alors une expression générique pour chaque terme de la somme et montre comment simplifier cette expression. Ensuite, il explique que la somme totale peut être calculée en utilisant la linéarité de la somme. Il effectue les calculs nécessaires et obtient la réponse finale. Il termine en encourageant les spectateurs à refaire l'exercice et à comprendre pourquoi certaines intuitions erronées ne fonctionnent pas.

Aire entre deux courbes

En utilisant la méthode QCM, nous pouvons éliminer certaines réponses évidentes. Nous devons trouver l'air délimité par trois courbes : y = e^x, y = 1 - e^x et l'axe y. On nous demande la valeur de R, qui est une aire, donc positive. On peut remarquer que log(e) = 1 et que log est croissant. Donc, log(2) sera inférieur à 1 car e (environ 2.7) est supérieur à 2. Donc, R sera négatif et peut être éliminé. En faisant un dessin, on peut voir que l'aire R existe entre les courbes e^x, 1 - e^x et l'axe y. Donc, la réponse R = 0 peut également être éliminée. En reliant les courbes e^x et 1 - e^x, on trouve un triangle circulaire dont nous voulons trouver l'aire. Nous devons donc trouver les bornes de l'intégrale, en trouvant la valeur de alpha qui est le point d'intersection des deux courbes. En utilisant l'équation E^(2alpha) = 1 - E^(2alpha), nous trouvons que alpha est égal à -log(2). En substituant alpha dans l'intégrale de E^(2x) - E^(2alpha), nous obtenons R = 1 + alpha = 1 - log(2). Ainsi, nous avons trouvé la réponse recherchée.

Exponentielle et ses tangentes

Dans cet exercice basé sur la géométrie et les fonctions, des tangentes sont tracées à la fonction y = e^(2x) aux points d'abscisses p et q. Les tangentes croisent l'axe des x aux points a et b respectivement. Il y a une relation entre a, b, p et q qui est exprimée par a - p = b - q. Pour comprendre l'énoncé, une figure peut être tracée. En résolvant les équations des tangentes, on obtient les relations a - p = -1 et b - q = -1. Ainsi, la réponse à l'exercice est a - p = b - q. Il est conseillé de rejoindre la communauté Discord pour obtenir de l'aide supplémentaire.

Une intégrale à borne variable !

Dans cette vidéo, le professeur revient sur un exercice d'intégration qui est tombé en 2021 lors de l'examen d'admission en mathématiques. Il explique comment résoudre l'exercice de manière optimisée en utilisant les astuces et les formules vues en cours. Le professeur commence par nommer les différentes variables et termes de l'exercice pour faciliter les calculs. Il souligne l'intérêt de bien connaître les primitives pour réussir cet exercice. Il rappelle également un tableau des primitives classiques à connaître, en insistant sur une formule générale puissance alpha, qu'il recommande de retenir. Cette astuce permet de résoudre des exercices plus complexes plus rapidement. Ensuite, il passe au calcul de l'intégrale en question. Il explique comment calculer I2A, la primitive de racine de x et de x2. Il utilise la formule générale puissance alpha pour la racine de x, ce qui simplifie le calcul. Il obtient ainsi l'expression de I2A. Le professeur pose ensuite l'équation I de A égale 5 et propose de la simplifier en multipliant par 3. Il remarque alors une relation polynomiale de degré 2 entre les termes. Il utilise donc une méthode bien connue pour résoudre ce type de polynôme. Il rappelle également une méthode alternative en utilisant la technique du X carré moins SX plus P. Il explique comment trouver les racines du polynôme et propose deux méthodes pour y parvenir. Enfin, le professeur revient sur la condition initiale de l'exercice qui stipulait que A doit être un nombre positif. En utilisant les valeurs trouvées pour les racines du polynôme, il élimine une des solutions. Pour conclure, le professeur écrit l'équation finale qui relie A à la valeur 5 et trouve la solution correspondante. Il rappelle également une formule générale permettant de trouver la racine d'une puissance donnée, ce qui peut être utile dans d'autres exercices.

Aire d'un dodécagone !

Dans cette vidéo, l'auteur présente un exercice de géométrie concernant un dodecagone régulier. Il explique que cela consiste en un polygone à 12 côtés, dont tous les côtés ont la même longueur et tous les angles internes sont égaux. Pour résoudre l'exercice, il suggère de diviser le dodecagone en triangles égaux et de calculer l'aire d'un de ces triangles. Il donne deux options pour le calcul de l'aire : soit en traçant une hauteur, puis en utilisant la formule de l'aire d'un triangle, soit en utilisant la formule des sinus. Il explique cette formule et montre comment l'utiliser pour obtenir l'aire de l'un des triangles. Ensuite, il multiplie cette aire par 12 pour obtenir l'aire totale du dodecagone, ce qui donne comme réponse 3. En conclusion, l'auteur souligne l'importance de comprendre les mécanismes d'accélération pour résoudre rapidement ce type d'exercice lors d'un concours.

Polynôme de degré 4 et nombres premiers

Le cours aborde un exercice du Mass Admission Test Docteur sur la factorisation et les nombres entiers. Il commence par analyser l'énoncé où il est demandé de factoriser le polynôme x^4 + 1. Il montre ensuite la factorisation en utilisant la formule (a^2 + b^2) = (a + b)^2 - 2ab. Il explique également qu'il est possible de factoriser tous les polynômes de degré supérieur à 2. Il montre ensuite que pour tout réel n, n^4 + 4 ne peut pas être un nombre premier. Il utilise une condition nécessaire pour être premier et montre qu'elle est vérifiée pour n=1, mais pas pour d'autres valeurs de n. Finalement, il conclut que l'ensemble des solutions de l'équation est réduit à l'entier 1.