Home

2BAC SM Maroc

Maths SM&SP

Analyse

Les fondements de la continuité

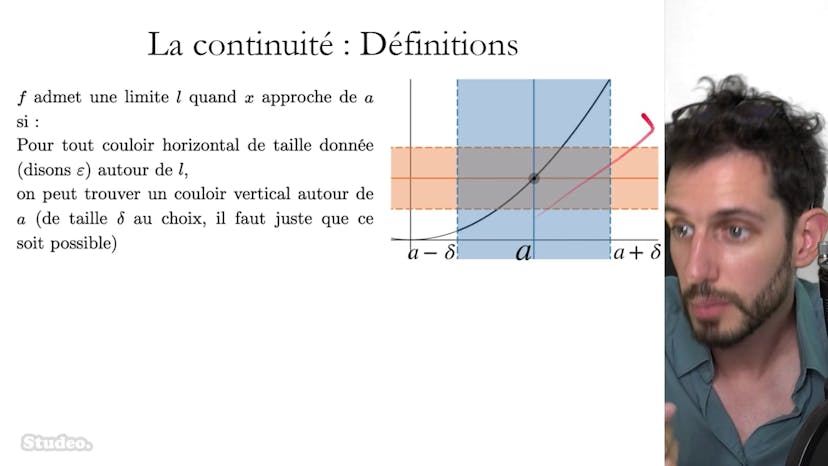
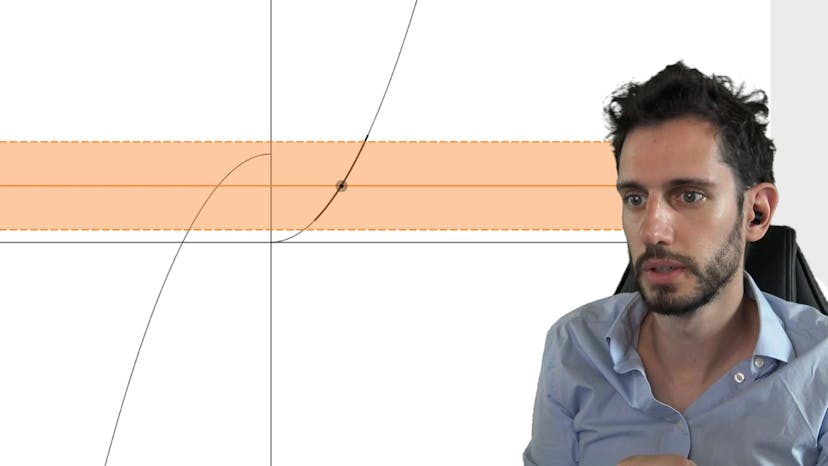
Ce cours porte sur le calcul d'une limite d'une suite définie par récurrence. La méthode consiste à trouver les points fixes de la fonction de récurrence et à vérifier si la suite converge vers l'un de ces points. Si la fonction est continue, alors la limite de la suite est un point fixe. Si la fonction n'est pas continue, cette méthode ne fonctionne pas. Il est important de justifier la continuité de la fonction pour appliquer cette méthode. Le premier terme de la suite peut également avoir une influence sur sa convergence, il est donc essentiel de le prendre en compte. Si la suite ne converge pas vers un point fixe, alors elle n'a pas de limite. Dans l'exemple donné, la fonction de récurrence est f(x) = x * (e^2 - x), et le point fixe est x = 0. La limite de la suite est donc 0 si le premier terme est positif. Dans un autre exemple où la fonction n'est pas continue, la suite ne converge pas vers le point fixe. Il est donc nécessaire de prendre en compte la continuité de la fonction pour utiliser cette méthode.

Alors on va s'intéresser dans cette méthode sur le calcul d'une limite quand la suite est définie par récurrence. Donc ça c'est quelque chose de très classique sur lequel vous allez tomber très souvent, ce qu'on appelle plus communément les suites définies en escalier. On va regarder précisément quelles sont les hypothèses à vérifier pour bien trouver la limite et bien la justifier. La méthode c'est la suivante, on va s'intéresser à une suite en particulier qui est définie par u0 égale 1 et un plus 1 égale un fois e2 moins un. On va voir aussi, c'est très important, que la convergence peut dépendre du premier terme. C'est très important de vérifier ce point. Pour une suite qui est définie par récurrence type un plus 1 égale f de un, où f est une fonction, c'est ça qui va faire qu'on a une suite en escalier. Si la suite est convergente vers une limite L, alors un plus 1 aussi. C'est là qu'on va passer à la limite de l'égalité un plus 1 égale f de un. On passe à la limite et on se dit que je prends la limite de un plus 1, ça fait L, et f de un, comme un est envers L, ça fait f de L. Donc L est nécessairement ce qu'on appelle un point fixe, qui est solution de l'équation f de x égale x. Ça c'est vrai, mais uniquement si f est continu, c'est un paramètre essentiel. Je vais revenir à la fin de la vidéo pour vous montrer que si f n'est pas continu, ça ne marche pas. C'est très important dans cette méthode de bien justifier la continuité. L'énoncé vous facilite la tâche, il vous dit qu'on admet qu'elle converge vers L. On ne justifie pas très bien pourquoi, mais c'est ça la clé, c'est de trouver les points fixes et les solutions sont parmi les points fixes. La solution de la limite est parmi les points fixes. Il peut y en avoir plusieurs, il faudra regarder au cas par cas si c'est lui, si c'est l'autre, etc. S'il n'y a pas de point fixe, il n'y a forcément pas de limite. La limite ne peut être que parmi ces points fixes. Je répète, s'il n'y a pas de solution à l'équation f2x égale x, s'il n'y a pas de point fixe, il ne peut pas y avoir de limite pour ce type de suite défini par occurrence avec une relation de type un plus un égale f2n. Là, on va étudier ces points fixes. On pose la fonction f2x égale x fois e2 moins x. Je résous f2x égale x. Attention, j'ai une relation de type x fois e2 moins x égale x. Ne divisons pas comme des barbares par x. On a le droit de diviser par un nombre que s'il est différent de 0. Il y a deux solutions, soit x égale à 0, et là je vois que c'est solution parce que ça fait 0 égale 0, soit il est différent de 0 et je divise par x et je trouve e2 moins x égale 1. C'est exactement la même solution. Même si on ne l'avait pas bien vu, on n'aurait pas fait d'erreur, mais dans le raisonnement, c'est ça. J'aurais pu tomber sur une solution différente de type x égale 1. Du coup, j'aurais eu deux solutions, x égale 0 et x égale 1. Ici, il n'y a qu'une solution possible à l'équation f2x égale x. Donc c'est x égale à 0. Comme on nous a dit qu'on suppose qu'elle est convergente, c'est la seule limite possible. Regardons comment ça se représente graphiquement. On fait la fameuse construction en étalier, je calcule u1, je le reporte sur l'axe des abscisses y égale x, je calcule u2, c'est u1 en abscisse, u2 en ordonnée, etc. Là, je vois que ça converge vers 0. Pourquoi ça dépend maintenant du premier terme u0 ? En fait, c'est essentiel. On va regarder sur le graphique pourquoi le premier terme est très important. Pourquoi le premier terme est essentiel ? On va le voir tout de suite. Si je bouge mon u0, tant que je suis supérieur à 0, ma suite converge. Par contre, si jamais mon u0 est négatif, je vois tout de suite que ma suite va diverger vers moins l'infini. Le premier terme est essentiel. Ici, ça ne marche que si u0 est positif. C'est pour ça qu'on dit que la solution est parmi les points fixes, mais elle ne l'est pas forcément. Là, j'ai un point fixe, ça ne veut pas dire que ma suite converge. Là, j'ai toujours la même fonction, pourtant j'ai changé mon premier terme et du coup, ma suite ne converge pas. Faire bien attention à ça. L'énoncé nous a bien dit qu'on suppose qu'elle converge. Si elle converge, je sais que c'est parmi les points fixes. J'en ai trouvé qu'un, donc c'est bon. Maintenant, pourquoi la continuité est vraiment essentielle pour ce type de fonction ? Je vais vous montrer un exemple pour que vous compreniez. J'ai créé une fonction qui est constante, qui est constante égale à 1, peu importe, de moins l'infini, jusqu'à un réel a. En a, elle est constante égale à 1. En a, je dis qu'elle vaut 2. Cette fonction est clairement discontinue. Le fait que je redis la définition de la continuité, c'est que la limite en x tend vers a de f de x est égale à f de a. C'est la définition de la continuité. Je vais vous montrer pourquoi cette fonction qui n'est pas continue Je trouve une suite particulière qui est un égale à a-1 sur n. Cette suite va être là, là, là, là, là, là, là, là, elle va converger vers a sans jamais être égale à a. C'est ça qui est très important. Elle va être tout le temps strictement inférieure à 1, mais elle va être de plus en plus proche. Cette fonction là, je la pose proprement, c'est f de x égale à 1, c'est x différent de a, f de x égale à 2, c'est x égale à a. Qu'est-ce qu'il se passe là ? Un est tout le temps strictement supérieur à a. Donc, quel que soit n, pour toutes les n appartenant aux entiers naturels, j'ai f de un qui sera égal à 1, jamais à 2. Or, un tend vers a, et donc là, je n'ai pas l'égalité entre la limite de f de un en plus infini qui vaut toujours 1, donc sa limite c'est 1 aussi, vu qu'elle est constante égale à 1, f de un, et donc c'est différent de f de a, qui est f de la limite des un. Donc typiquement, où est-ce que ça poserait problème dans mon raisonnement, si je remonte un peu, c'est, pardon, c'est, je ne trouve pas, c'est ici, voilà. C'est là, là j'ai un plus un égale à f de un, et vous voyez, qu'est-ce que j'ai fait comme raccourci, j'ai dit, bon ben un tend vers l, donc f de un tend vers f de l. Ben voilà, ça c'est faux si f n'est pas continue. J'ai besoin de la continuité, par contre si j'ai la continuité, c'est bon. Donc voilà pourquoi il nous faut absolument la continuité. Ce sont des choses que vous étudierez pour ceux qui continuent en prépa l'année prochaine, ce qu'on appelle permuter la limite des f, en fait c'est ce qu'on a fait, on a écrit que limite de f de un égale à f de limite de un. Vous étudierez ça précisément l'année prochaine, formellement, mais en tout cas voilà pourquoi ce point est très important. Voilà pour cette méthode, si vous avez des questions sur ce point un peu technique, n'hésitez pas à aller voir la FAQ.

Continuité et suites 1

RELATED

Recommended videos

Déf formelle

Discontinuités : exemples

Fonctions usuelles