Home

2BAC SM Maroc

Maths SM&SP

Analyse

Les fondements de la continuité

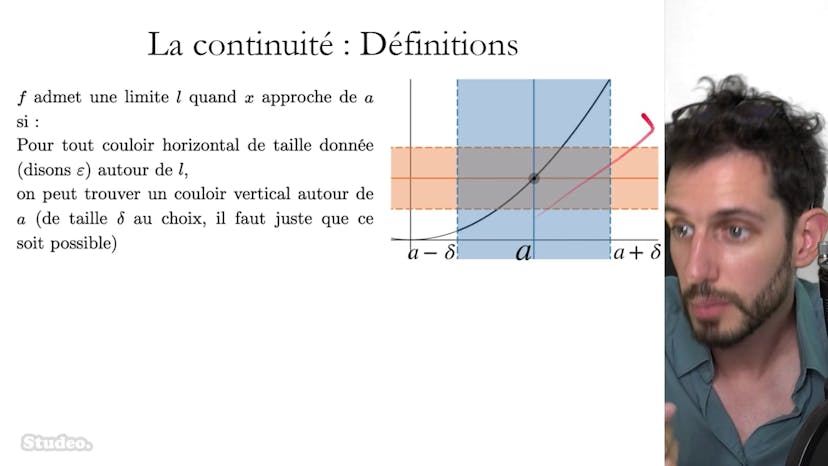
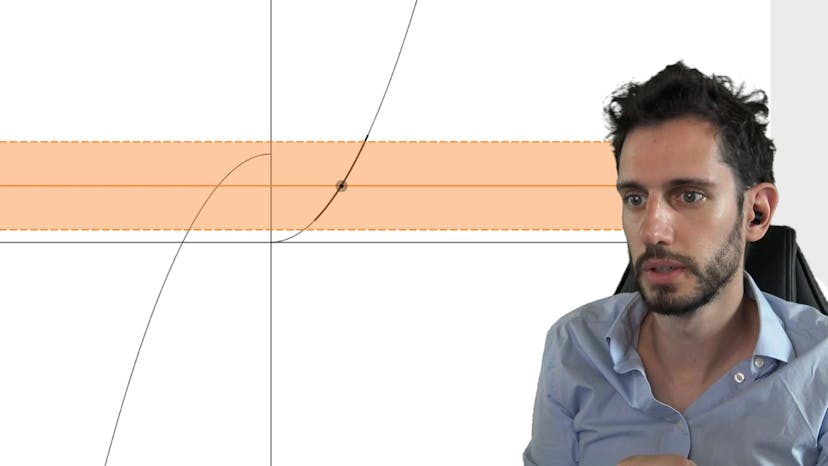
Dans ce cours, nous étudions graphiquement le nombre de solutions de l'équation E-x² = E2x-1. Nous observons les courbes des deux fonctions E-x² et E2x-1. La courbe de E-x² est une courbe en cloche de probabilité. Nous remarquons que la fonction noire est au-dessus de la fonction rouge pour les nombres négatifs, mais qu'il y a un changement de comportement aux nombres positifs où les deux fonctions s'intersectent.

Nous séparons ensuite l'étude en deux parties : R- (les nombres négatifs) et R+ (les nombres positifs). Sur R-, nous démontrons que la fonction en cloche E-x² est strictement supérieure à l'autre fonction, ce qui prouve qu'il n'y a pas de solutions à l'équation dans cette plage de nombres.

Sur R+, nous posons f2x = E-x² - E2x-1 et étudions sa décroissance. En utilisant les propriétés de l'exponentielle, nous montrons que f2x est strictement décroissante sur 0 plus l'infini.

En utilisant le théorème des valeurs intermédiaires, nous concluons qu'il existe une unique solution à l'équation sur R+. Finalement, nous concluons qu'il n'y a pas de solutions sur R- et une unique solution sur R, ce qui confirme notre intuition graphique.

En résumé, l'équation E-x² = E2x-1 a une unique solution sur l'ensemble des réels.

On va étudier ce truc-là, conjecturer graphiquement le nombre de solutions de l'équation. Alors graphiquement, j'ai préparé, on a E-x², E2x-1, voilà les deux fonctions. Si je zoom un peu, donc ça c'est E2x², en fait c'est la courbe en cloche de probabilité, c'est un classique. La courbe en cloche c'est E2-x² pardon. Donc après la courbe en cloche en pro bas elle a des petites variantes mais c'est celle-ci. Et E2x-1 qui est en fait la fonction exponentielle mais décalée de 1 sur l'axe Y. Bon graphiquement, c'est assez simple, on a l'impression qu'il y a une solution ici. En 0.552 je sais pas quoi. En gros on a une solution, on va essayer de la démontrer, on voit plusieurs choses intéressantes sur le graphique. C'est-à-dire que pour R-, pour les nombres négatifs, clairement la fonction noire est au-dessus de la fonction rouge. Et pour R+, il y a un changement de comportement où la fonction noire est au-dessus de la fonction rouge au début, puis elle s'intersecte et le comportement change. Voir cette intuition graphique peut vous expliquer assez vite aussi les questions suivantes. Montrer que pour tout réel négatif, il y a quelque chose qui se passe. Et ensuite on prend F définit sur R+, donc on sépare en deux l'étude. On sépare en deux parce qu'en effet là, on a une étude où on voit qu'il y a deux comportements sur R- et sur R+. Alors si je suis exact, il y a deux comportements avant le point d'intersection et après, mais sur R-, en tout cas, c'est l'endroit, c'est la zone où la fonction noire est croissante. Donc ça vaut le coup peut-être de séparer en deux comme ça. C'est pour ça que la question 1 vous dit pour tout réel négatif, montrez qu'on a bien la fonction en cloche E-x² qui est supérieure à l'autre. Là, il faut se rappeler de ce que ça veut dire x- pour l'exponentiel. Donc on va le faire tout de suite, petit 2. x-, qu'est-ce que ça implique pour la fonction en exponentiel qui est une fonction strictement croissante ? Ça implique que E2x est plus petit strict que E0 égale 1. Ce qui implique que E2x-1 soit négatif strict. Donc, tout bêtement, juste par le fait que E2x-1 est négatif, et bien il est strictement plus petit que E2-x². La question est démontrée. Donc sur R-, c'est réglé. Elles ne vont pas se croiser, il n'y a pas de solution à l'équation parce que, tout bêtement, E2-x² est juste supérieure stricte à ça. Il n'y a pas moyen qu'elle soit égale vu qu'elle est toujours supérieure stricte. Maintenant, on va essayer de gérer sur R+, ce qui se passe. Donc méthode classique, quand on vous demande de montrer une égalité comme ça, posez une fonction, on met tout à gauche, et on pose la fonction appropriée. Donc on met tout à gauche, ça veut dire qu'on fait moins E2x-1 de chaque côté, et on va étudier f2x égale 0, si vous voulez. Donc on met tout à gauche pour avoir 0 ici, et on utilise la fonction a. On va montrer que f est strictement décroissante sur 0 plus l'infini. Alors ça, ça peut être gérable de deux manières. Une manière, ça peut être de dire E2-x² sur 0 plus l'infini, c'est en gros E2-x sur R+, c'est pareil. Donc ça décroît. Avec elle, on retire, ou on ajoute, si vous voulez, la fonction moins E2x, qui est aussi décroissante. Donc en fait, on a une somme de fonctions décroissantes, le tout est décroissant. Ça a un peu galère peut-être à faire, on pourrait juste dire aussi f dérivable. Pourquoi ? Parce que quand on a R+, tout ça c'est positif, donc ça devient négatif avec le moins. Ça c'est positif par définition, donc le tout est négatif. Strict. Strict parce que ça ne peut jamais être égal à 0. Donc E2x est négatif, et donc f est décroissante. Limite de f en plus l'infini. Donc c'est en gros x² est envers plus l'infini, donc moins x² est envers moins l'infini. Donc l'exponentiel est envers 0, moins l'infini quand x est envers plus l'infini. Tout simplement parce que l'exponentiel est envers plus l'infini, et qu'un moins ça donne ça. Et donc on a dit limite. On va dédire le nombre de solutions de l'équation. C'est parti, on trace un petit tableau de variation sur R+. Je suis en train de tracer f' dans le tableau, vu qu'il suffit juste de dire qu'elle est décroissante. Enfin, on a vu qu'elle était négative tout le temps, donc je serais juste en train d'ajouter une ligne où je mets un moins partout. Donc ça descend. En 0, la fonction vaut 1, moins 1, 0, plus 1, égal 1. La fonction est continue par le théorème des valeurs intermédiaires. Je sais qu'il va exister, donc il faudrait l'appliquer de manière très correcte. Donc allez voir mes vidéos sur le théorème des valeurs intermédiaires pour une rédaction idéale. Mes trois hypothèses pour le théorème des valeurs intermédiaires dans le cas bijectif. Donc j'ai trois hypothèses, celle-ci, celle-ci et celle-ci. Le fait que la valeur qu'on cherche, donc f2x égal 0, est bien comprise entre les deux valeurs extrêmes. Le fait que f soit continue. Le fait qu'elle décroisse. Le E à l'envers prouve qu'il existe. Le point d'interrogation, d'exclamation pardon, pour un unique. Alpha appartient à 0 plus l'infini tel que f2alpha égal 0. On peut l'écrire ici, c'est la valeur. Ou f, pour laquelle f traverse l'axe des abscisses. Donc voilà, vous appliquez votre TVI. Et la conclusion de l'exercice c'est quoi ? Sur R- il y a zéro solution. A cause de la question 1, on a bien démontré que cette égalité est impossible. Parce que ce membre ici est toujours supérieur à celui-ci. Donc sur R- il ne se passe rien. Et sur R+, on a trouvé une unique solution. Conclusion, sur R, on a une unique solution. Comme l'instruction graphique nous l'avait montrée. Voilà, parfait.

TVI et expo

RELATED

Recommended videos

Déf formelle

Discontinuités : exemples

Fonctions usuelles