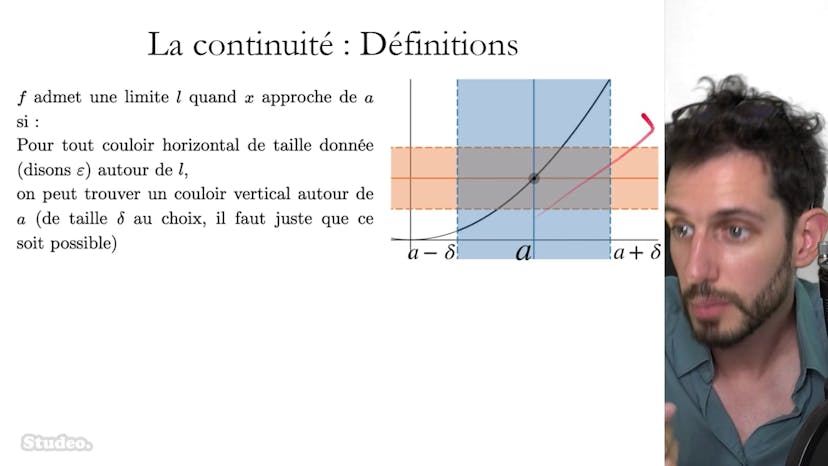
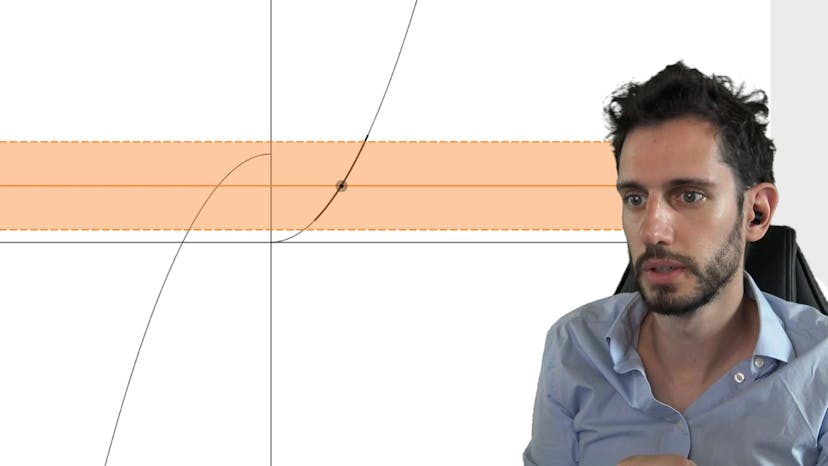
All subjects
All subjects
 All subjects
All subjects
TVI et calculs costauds !
La fonction f(x) = 2/(e^x + e^(-x)) représente une somme d'exponentielles positives strictes, ce qui exclut la possibilité d'obtenir une valeur égale à zéro. En regardant graphiquement le nombre de solutions de l'équation f(x) = x, il est clair qu'il n'y a qu'une seule solution unique. Pour montrer que la fonction g(x) = f(x) - x est décroissante, nous commençons par dériver la fonction f(x) et simplifier. La dérivée de f(x) est -2(e^x - e^(-x))/(e^x + e^(-x))^2. Après des calculs plus avancés, nous obtenons que la dérivée de g(x) est égale à -2(e^(2x) + 1)(e^(-2x) - 1)/(e^(2x) + e^(-2x))^2, ce qui est toujours négatif. Par conséquent, nous pouvons conclure que g(x) est décroissante. En utilisant le Théorème des Valeurs Intermédiaires, nous pouvons affirmer qu'il existe un unique nombre alpha tel que f(alpha) = alpha. Ainsi, l'équation f(x) = x admet une seule solution.