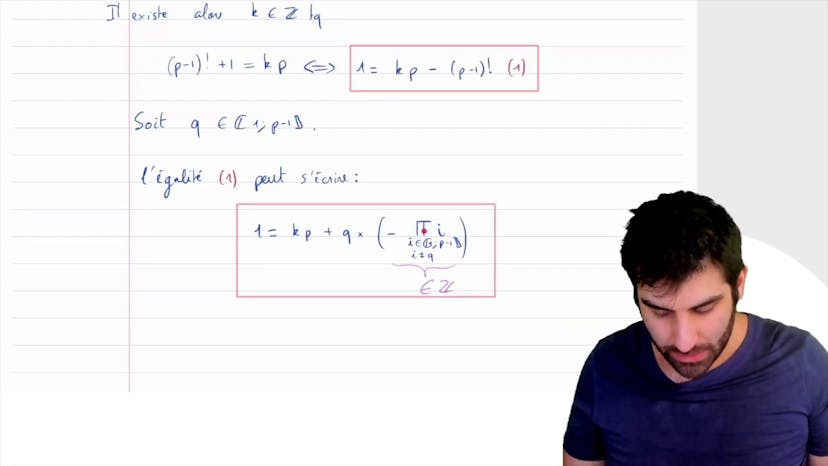Home

MPSI/PCSI

Maths

Algèbre

Nombres premiers

Dans cette vidéo, on aborde le sujet des nombres de Mersenne. 
Le premier objectif est de démontrer que si  a^(n-1) est premier, alors a est égal à 2 et n est premier. 
Pour cela, on factorise a^(n-1) avec a-1, a^(n-2), ..., jusqu'à 1. On remarque que 1-1 divise a^(n-1), tandis que a-1 est différent de a^(n-1) car n est supérieur ou égal à 2. Donc a-1 est égal à 1, ce qui implique que a est égal à 2. 
Ensuite, il faut prouver que n est premier. On note n comme p*q, et on réécrit une égalité factorisée avec 2^(n-1). On observe que 2^(p-1) divise 2^(pq-1), qui est égal à 2^(n-1). Donc, si 2^(p-1) est égal à lui-même, cela signifie que p est égal à n. Ainsi, q est égal à 1 dans cette factorisation. De plus, si 2^(p-1) est égal à 1, cela entraîne que p est égal à 1. Donc, q est égal à n. Ainsi, dans tous les cas, n est un nombre premier. 
Ensuite, on doit vérifier que M11 n'est pas premier. On calcule M11, qui est égal à 2^11 - 1, soit 2047. On peut le décomposer en 23 fois 89, ce qui prouve que ce n'est pas un nombre premier. 
Le but de cette question est de comprendre pourquoi on nous l'a posée. On a vu précédemment que si un nombre de Mersenne est premier, alors la puissance n est aussi premier. Cependant, on vient de prouver le contre-exemple que si n est premier, alors 2^11 - 1 n'est pas premier. Donc, on a démontré que la réciproque ne marche pas.

Salut, bienvenue dans cette vidéo sur les nombres de Mersenne. Dans la première question, on nous demande de montrer que si a puissance n-1 est premier, alors a égale 2 et n est premier. On va commencer par montrer que a est égal à 2. On peut factoriser a puissance n-1 par a-1, facteur de a puissance n-1 plus a puissance n-2, etc., jusqu'à a et 1. C'est une factorisation qu'il faut absolument savoir faire. Quand on a un nombre à une certaine puissance, on peut le factoriser comme ça. On observe que 1-1 divise a puissance n-1. Par contre, a-1 est différent de a puissance n-1 parce que n est supérieur ou égal à 2. Sinon, on aurait pu conclure que n égale 1, tout simplement. Mais n, on nous dit qu'il est plus grand que 2. Donc, a-1 est différent de a puissance n-1. Étant donné qu'a puissance n-1 est un nom premier, un diviseur de a puissance n-1, c'est soit 1, soit lui-même. On a exclu le cas où c'est lui-même. Donc, nécessairement, a-1 est égal à 1. Donc, a est égal à 2. Assez rapide. Maintenant, il faut montrer que n est premier. On va noter n comme p fois q. Le but va être de montrer que p ou q est nécessairement 1 ou n. Là, on va réécrire une égalité factorisée du même genre avec 2 puissance n-1 qui est égale à tout ça. Sauf que là, notre a, on l'a pris comme étant 2 puissance p. Donc, 2 puissance p à la puissance q. C'est 2 puissance p moins 1 fois 2 puissance p puissance q moins 1 plus 2 puissance p puissance q moins 2, etc. jusqu'à 1 à la fin. Là, on observe que 2 puissance p moins 1 divise 2 puissance pq moins 1. 2 puissance pq moins 1, c'est 2 puissance n moins 1. Donc, 2 puissance p moins 1 divise 2 puissance n moins 1 qui est premier par hypothèse. Parce que a, on a dit que c'était 2. Et on a supposé que a puissance n moins 1 était premier. Donc, 2 puissance p moins 1 divise un nom premier. Même conclusion que tout à l'heure, soit c'est 1, soit c'est lui-même. Donc, si c'est lui-même, ça veut dire que, nécessairement, p est égal à n. Donc, q est égal à 1 quand on regarde cette factorisation. Et maintenant, si 2 puissance p moins 1 est égal à 1, alors, ça veut dire que 2 puissance p vaut 2. Donc, nécessairement, p égale 1. Et du coup, en regardant ça, q est égal à n. Donc, c'est les seules possibilités qu'on a. Si on écrit n comme p fois q, on a soit p égale n, q égale 1, soit l'inverse, p égale 1, q est égal à n. Donc, dans tous les cas, n est un nombre premier. Ensuite, question 2, on nous dit, on note Mn, donc le nème nombre de Mersenne, 2 puissance n moins 1. Il faut vérifier que M11 n'est pas premier. Donc, on calcule. M11, c'est 2 puissance 11 moins 1. Ça fait 2047. Et ça, on peut l'écrire comme 23 fois 89, qui n'est pas premier. Alors, la question, en réalité, bon, c'est pas juste de vérifier ça, vérifier qu'un nombre est premier ou pas, c'est pas très intéressant, c'est essayer de comprendre pourquoi on nous a demandé ça. Parce que, ce qu'on a vu tout à l'heure, c'est que, si a puissance n moins 1, du coup, en réalité, c'est 2 puissance n moins 1, si un nombre de Mersenne est un nombre premier, alors, nécessairement, la puissance n, du coup, est un nombre premier. D'accord ? C'est ça qu'on observe. Mais, on vient de montrer que la réciproque n'est pas vraie. On vient de montrer que, si n est un nombre premier, 2 puissance 11 moins 1 n'est pas un nombre premier. Donc là, on a montré, dans la première question, que, si le nombre de Mersenne est un nombre premier, alors, nécessairement, le n est un nombre premier. Mais, dans la question 2, on vient de montrer un contre-exemple de la réciproque, du coup, qui dit que ça ne marche pas. Donc, voilà pour cet exercice.

Nombres de Mersenne

RELATED

Recommended videos

Nombres de Fermat

Théorème de Wilson