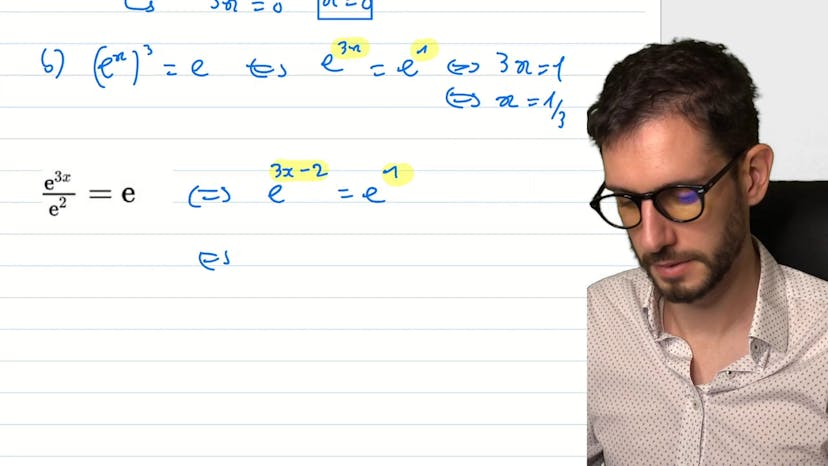Home

Première

Maths

Analyse

Exponentielle

Dans ce cours, nous apprenons à maîtriser la simplification des expressions exponentielles. Voici quelques exemples :

- Pour l'expression E de 2 fois E de moins 1, nous simplifions en E puissance 1, soit E.
- Pour l'expression E de 3 fois E de moins 3, nous simplifions en 1.
- Pour l'expression E de 4 sur E de moins 2, nous pouvons déplacer la puissance du dénominateur au numérateur en changeant le signe, ce qui donne E de 6.
- Pour l'expression E de x plus 1 au carré, nous utilisons les identités remarquables pour développer l'expression en E de 2x plus 2 E de x plus 1.
- Nous soulignons l'importance de reconnaître que E de 2x peut être lu comme un carré, car cela peut être utile pour résoudre des équations de degré 2.

Nous notons également que E de x moins 1 multiplié par E de x plus 1 est égal à E de 2x moins 1, et que E de x moins E de moins x au carré est égal à E de 2x moins 2 fois E de x fois E de moins x plus E de moins 2x.

Il est important de pratiquer ces simplifications et de s'entraîner sur des exemples. Si vous avez des questions ou besoin d'explications supplémentaires, n'hésitez pas à me les poser. Au revoir et à bientôt pour une prochaine leçon.

Méthode typique, maîtriser la simplification d'exponentielle. Bon, là j'en ai mis plein plein plein, honnêtement je ne vais pas toutes les faire mais je vais vous montrer un peu comment faire ça rapidement et sans trop de difficultés. Ce qu'il faut penser c'est, en gros, c'est une fonction puissance. Donc tout ce que vous avez appris à faire, en gros en troisième si je ne me trompe pas, vous savez le faire là, il n'y a pas de raison, si vous l'avez fait en troisième vous saurez le faire là vu que c'est la même chose. Donc tout ce qui est 10 puissance, quelque chose, les propriétés sur les puissances de 10 par exemple, vous l'appliquez avec E, c'est pareil. Donc petit a, E de 2 fois E de moins 1, ça égale à E de 2 moins 1, ça fait E puissance 1, ça fait E, on peut l'écrire. Petit b, E de 3 fois E de moins 3, ça fait E de 0, ça fait égal à 1. Ensuite petit c, on a E de 4 sur E de moins 2, hop, on peut faire monter la puissance au dessus, non pas au dénominateur mais au numérateur, mais en changeant son signe. Tout ça, ça fait E de 6. Et ensuite ça se complique un petit peu, petit d, on dit E de x plus 1 le tout au carré, donc là c'est une petite révision, vraiment on plaint dans la troisième ou la seconde, là c'est une révision de vos identités remarquables. Comme quoi ces trucs là sont vraiment, on vous saoule avec en fin de collège, mais il faut vraiment les connaître parce qu'elles tombent partout. Donc ça fait E de x, alors j'ai été un peu vite. Si on l'écrit en plusieurs étapes, ça fait E de x carré plus 2 fois E de x fois 1 plus 2 E de x, plus 1 au carré, et E de x au carré, on connaît nos règles de puissance, ça fait E de 2x plus 2 E de x plus 1. Ce qui est intéressant avec ça, c'est pas de développer, développer c'est facile. Ce qui est intéressant c'est de se dire, attention, quand j'ai un E de 2x maintenant, pensez que 2x peut être lu comme un carré. C'est à dire qu'il y a des exercices où on vous dira de résoudre des équations, il faudra repérer une structure de quoi ? De polynômes du degré 2. Polynômes du degré 2 qui vont vous hanter pendant toute la première, la terminale, ils seront partout. Il y aura des exos, on en verra peut-être, où vous aurez 3 fois E de 2x plus 2 E de x moins 5 égale 0. Trouvez les solutions ! J'ai mis moins 5 parce que j'ai repéré une racine évidente 1 là. Il faudra dire, attention, je reconnais la structure polynomiale, comme ça. Je pose grand x égale E de x et j'ai 3x2 plus 2x moins 5 égale 0. Et ça je sais résoudre. Et en gros tout ça, votre capacité à faire ça sera uniquement là si vous savez reconnaître que E de 2x est E de x au carré. Alors c'est peut-être évident, je ne sais pas, mais moi c'est ça le truc qu'il faut retenir ici. Petite E, E de x moins 1, E de x plus 1, bon honnêtement ça c'est une identité remarquable également. Donc E de x moins 1, E de x plus 1, c'est donc du a2 moins b2, ça fait E de 2x. C'est E de x au carré donc E de 2x je le mets directement, moins 1. Enfin E de x moins E de moins x le tout au carré. Donc ça c'est intéressant, moins E de moins x, enfin c'est intéressant. Au carré égale E de 2x, moins 2 fois E de x, E de moins x, plus E de moins x au carré moins 2x. Et ça ça fait quoi ? E de 2x moins 2 fois E de x fois E de moins x, ça fait 2 fois 1, moins 2 plus E de moins 2x. Alors celui-là dans l'autre sens, à factoriser ce n'est pas évident, il faut le voir. Mais en tout cas à développer c'était simple. Je vous ai montré pas mal d'exemples, c'était pour moi un peu histoire de faire un petit bilan là-dessus. Je n'ai pas grand-chose à dire à part il faut pratiquer. Quelques exemples très simples. Je vous ai mis tout cela en plus, amusez-vous, vous entraînez dessus. Posez-moi des questions si sur un point spécifique vous n'avez pas compris ou vous pensez que vous avez besoin d'un peu plus d'explications, de clarté ou d'exemples. Sinon je vous retrouve dans une prochaine méthode. Bye bye.

Simplifier des expressions avec exp

RELATED

Recommended videos

Propriété fondamentale : démo

Résoudre des équations