Home

MPSI/PCSI

Maths

Analyse

Continuité sur un segment

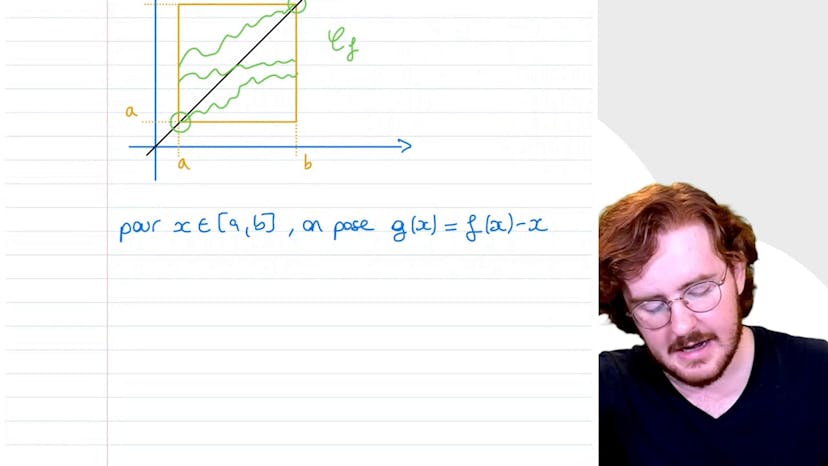
Dans cet exercice sur les fonctions continues sur un intervalle, Paul démontre que la fonction f est bornée sur R. La fonction f est définie sur R par un polynôme de degrés pairs et une exponentielle de moins x carré. Pour démontrer que f est bornée, il détermine d'abord les limites de la fonction en plus et moins l'infini en utilisant les règles de composition des limites. Puis, il démontre qu'il existe un réel a et un réel b tels que la fonction f est bornée sur l'intervalle a, b pour chaque x supérieur ou égal à a et chaque x inférieur ou égal à b. En utilisant la continuité de f sur l'intervalle a, b, il conclut que f est bornée sur R en utilisant le terme des bornes atteintes.

Salut c'est Paul, on se retrouve pour cet exercice sur les fonctions continues sur un intervalle. Donc on a f, la fonction définie sur R par f de x, égale un polynôme ici de degrés avec que des degrés pairs, et une exponentielle de moins x carré. Et le but ça va être de démontrer que la fonction est bornée sur R et on a des questions pour nous aider à y arriver. Donc déterminer la limite de f en plus de l'infini et moins de l'infini. En fait là c'est très simple, on utilise les règles de composition des limites, enfin des règles de Gauss-Huyslave et les limites. Donc la limite du polynôme c plus l'infini en plus l'infini, et la limite de l'exponentielle c0 en plus l'infini. Les limites sont pareilles en moins l'infini, sont les mêmes. Et d'après les croissances comparées, l'exponentielle l'emporte toujours, donc les limites l'emportent sur le polynôme. Donc d'après les croissances comparées, les limites en plus l'infini et moins l'infini de f sont 0. Maintenant on va démontrer qu'il existe un réel a strictement supérieur à 0, tel que pour toute x supérieur ou égal à a, on a f2x inférieur ou égal à 1, donc la valeur absolue de f2x inférieur ou égal à 1. En fait là on peut remarquer que c'est la définition de la limite, ici, pour epsilon reçoit 1. Et bien voilà, on l'écrit. On a cette limite, que x tend vers plus l'infini, f2x tend vers 0. Donc d'après la définition de la limite pour epsilon reçoit 1, il existe un a strictement supérieur ou égal à 0, donc le a normalement dans la définition de la limite c'est un réel, mais pour une limite en plus l'infini on peut choisir qu'il soit strictement supérieur ou égal à 0, ça ne change rien, sinon on peut prendre le maximum de 1 et de ce a, pour choisir un a qui est bien strictement supérieur ou égal à 0. Donc on a, avec la définition de la limite, on a directement la réponse à la question. Pour la question 3, c'est la même chose, mais avec un réel b et strictement inférieur ou égal à 0. Pour toute x inférieure ou égal à b, on a la valeur absolue de x est inférieure ou égale à 1, sauf que là c'est la définition de la limite en moins l'infini qui nous le donne. Maintenant on va démontrer que la fonction f est bornée sur R. On va remarquer que d'après les questions 2 et 3, là on a prouvé que la fonction était bornée à chaque fois sur, ici, moins l'infini b et a plus l'infini. Or, maintenant on va prouver la continuité sur l'intervalle b, a. Donc f est continue, elle est continue sur a, b, mais en fait ce qui est important c'est que c'est le segment a, b. Là vous voyez que j'ai pas pris, j'aurais pu prendre b, a ou vert, mais j'ai choisi intentionnellement d'inclure a et b, parce qu'on va plus ou moins utiliser le terme des bornes atteintes, qui dit que si une fonction est continue sur un segment, cette fonction est bornée sur ce segment et elle atteint ses bornes. Mais là on a juste besoin du terme des bornes atteintes, on s'en fiche pour là. Donc f est bornée sur a, b, ainsi là on a bien R tout entier. Donc R, f est bornée sur R et c'est la fin de cet exercice. Donc on se dit à la prochaine fois!

Fonction bornée

RELATED

Recommended videos

Variations et théorème des valeurs intermédiaires

Point fixe et continuité