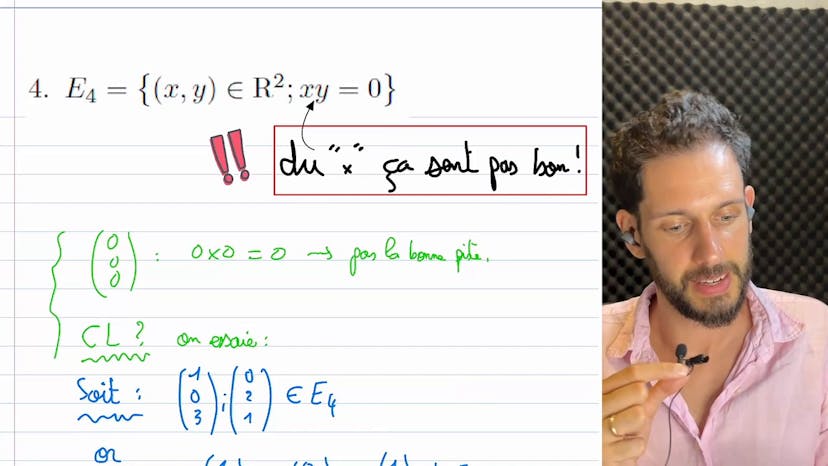Home

MPSI/PCSI

Maths

Algèbre

Espaces vectoriels et sous-espaces vectoriels

Dans ce cours, nous avons étudié différentes techniques pour déterminer si des ensembles sont des espaces vectoriels. Nous avons notamment examiné des exemples où les ensembles étaient définis par l'intersection ou l'union de deux ensembles.

Dans le cas d'une intersection, nous avons pris l'exemple de deux plans. Lorsque les plans sont distincts et non parallèles, leur intersection est une droite. Cette droite, passant par le point 0, peut être considérée comme un espace vectoriel de dimension 1.

En revanche, dans le cas d'une union, nous avons souligné la difficulté de prouver la conservation par combinaison linéaire. Nous avons pris l'exemple de deux plans, où il est possible de trouver des éléments dont la somme ne se trouve dans aucun des deux plans. Cela montre que l'union de ces deux ensembles n'est pas un espace vectoriel.

Pour démontrer ces résultats, nous avons utilisé une approche mathématique. Par exemple, pour le cas de l'intersection de deux plans, nous avons résolu un système d'équations pour obtenir une paramétrisation de la droite d'intersection.

Il est important de toujours se poser des questions et réfléchir à la situation avant de se lancer dans des calculs. Cette intuition initiale permet de mieux comprendre le problème et de choisir la bonne démonstration.

En conclusion, l'intersection de deux ensembles est souvent un espace vectoriel, tandis que l'union ne l'est généralement pas. Il faut cependant utiliser des méthodes mathématiques pour prouver ces résultats.

N'hésitez pas à poser vos questions en commentaire et restez attentifs pour nos prochaines vidéos.

Pour déterminer si des ensembles sont des espaces vectoriels, on a vu plusieurs techniques. Ce qui est intéressant maintenant, c'est qu'il y a des exemples ici, deux exemples dans l'exercice, où on a des ensembles non définis par un seul ensemble, mais par l'intersection de deux ensembles, ou l'union de deux ensembles. Donc un truc un peu plus différent. Réflexion intuitive. Le cas numéro 6, on a un plan ici, un plan ici. L'intersection des deux, on la connaît. En fait là, j'appelle vos connaissances de géométrie 3D de terminal, le croisement de deux plans, c'est une droite. À part si les plans sont parallèles. Dans ce cas, c'est l'ensemble vide. Vous me dites si les plans sont confondus, ok, bon, il y a le cas confondu, mais clairement ils ne sont pas confondus, les équations sont différentes. Donc soit ils sont parallèles, ok, ensemble vide, sincèrement les vecteurs normaux n'ont pas l'air d'être les mêmes, donc je n'ai pas l'impression qu'ils soient parallèles. Les vecteurs normaux, c'est quoi ? 2, 3, 5, 1, 1, 1, ça ce n'est pas le même vecteur. Donc l'intersection des deux est une droite. Une droite, ça sent bon normalement. Ça sent bon parce qu'une droite, sachant que le point 0 est là-dedans, l'intersection des deux sera une droite qui passe par 0. En gros, 0 appartient au 2, donc il appartient à l'intersection, donc c'est une droite qui passe par 0, ça sent l'espace vectoriel de dimension 1. L'espace qui passe par 0, ça semble bien. Par contre, l'union ici, je vous fais vraiment de l'intuition et après je vous fais la démonstration, ma démo ce n'est pas juste ça. Deux plans, c'est quoi ? L'union, c'est l'ensemble des trucs qui sont dans ce plan. Union, l'ensemble des trucs qui sont dans ce plan. Ok, ben ça, moi, je suis un peu inquiet pour, comment dire, je suis un peu inquiet pour la conservation par combinaison linéaire, parce que si je prends un élément de E7 qui se trouve être là, en rose, et je fais la somme avec un élément de cette deuxième partie de E7, qui est la flèche rouge, ça c'est la flèche verte, c'est un truc qui n'est ni dans l'espace rose, ce serait ça, ni dans l'espace rouge. Tout de suite, là, je sens que ce n'est pas bon. Il faut que je pense qu'en gros, ce que ça veut dire, c'est cette union. Union, c'est ça ou ça, et je vois direct que la somme de deux éléments peut être en dehors de ces deux-là. Donc compliqué. Je vous donne ça parce qu'il faut toujours réfléchir. Il faut toujours avoir un premier élément de savoir à peu près où on va comme ça, comprendre la situation dès que c'est possible. Si vous ne le faites pas et que vous vous lancez que dans les calculs sans visualiser, vous ne saurez pas même comment prendre la démonstration. Ici, je sais que je vais montrer plutôt que ça, c'est un espace vectorel, et montrer plutôt que ça, ce n'est pas grâce à mon analyse intuitive. Donc faisons la démonstration maintenant pour le petit 6. Je pose un élément. X, Y, Z appartient à E6. Si et seulement si, à la fois ça et ça. Petit système de deux équations. Je ne me prends pas trop la tête. C'est deux équations, trois inconnues, mais il ne faut pas s'inquiéter, c'est normal. Il n'y a pas une solution unique. Encore une fois, le croisement de deux plans ce n'est pas un point unique, donc c'est normal que je n'ai pas trois équations ici. Par contre, je peux exprimer un peu tout. Je peux faire la somme, je fais des combinaisons. Je fais cette équation moins deux fois celle-là pour tirer les X. J'obtiens 5Y égal 7Z. Ici j'ai X moins Y plus Z que je ne touche pas. Donc j'ai Y égal 7 5e de Z. Je mets ça, ça fait Y moins Z, 7 5e de Z moins Z, et j'obtiens ça. X égal 2 5e de Z, Y égal 7 5e de Z. En gros, c'est une espèce de paramétrisation de droite. Le plus simple, c'est d'essayer d'écrire X, Y, Z dans le vecteur. Comme j'ai ça, je peux dire, en me rapportant un peu, voire une vidéo précédente à une écriture en vect, je peux dire que le vecteur s'écrit X, Y, Z égal 2 5e, 7 5e de Z, Z. Je sors le Z et j'ai une constante fois 2 5e, 7 5e, 1. Je n'aime pas les 5e, donc je sors aussi un 5e, et ça me donne, en gros, 7 5e fois 2 7 5. Donc n'importe quel vecteur de X s'écrit comme une combinaison de 2 7 5. Donc, n'importe quel vecteur qui appartient à E6 appartient avec de ça. Vect de 2 7 5, c'est une droite vectorielle. Donc, E6 c'est un vect, c'est donc un espace vectoriel. C'est réglé. Pour la question 7, on a dit, on va essayer de trouver un exemple d'un élément là, un élément là, je prends la somme qui n'est dans aucun des deux. Je vais le faire un peu à la mano. J'appelle ça A, j'appelle ça B. Le but c'est de trouver un élément de A et un élément de B dont la somme n'est dans aucun des deux. Ça ne va pas être trop compliqué. Donc, astuce pour trouver ce genre de truc. Je ne sais pas si j'ai mal mis, si vous ne voyez pas mon écran depuis tout à l'heure, j'espère que si. Bien placer des zéros, c'est-à-dire, par exemple, quand on cherche des vecteurs un peu comme ça au pifomètre, mettre des zéros pour simplifier un peu. C'est-à-dire, c'est plutôt cool de mettre des zéros parce que ça vous évite trop de complexité. Donc, je prends un peu au pif, je prends 5, 0, 2 qui a l'air de marcher. En gros, je m'arrange, je mets zéro ici, je fais 3, 2, 1, 0 et je dis bon, si je mets 5 et 2, ça fait zéro. Je mets un zéro ici et je prends ensuite 1 et 1, ça fait zéro. Voilà, donc là je suis sûr et garanti de trouver des éléments facilement. Or, je prends la somme. Là, je prends la somme et vous allez me dire mais comment tu savais que la somme ne serait pas dans les deux plans ? En gros, je me dis que si j'en prends deux au pif, il y a quand même une chance très très faible que la somme soit sur un des deux plans. Enfin, c'est quasiment impossible. Donc, je prends au pif et je teste si vous voulez. J'ai 6, 1, 2 qui est la somme. Est-ce que 6, 1, 2 appartient à grand A ? Non. Je prends les coordonnées et je vérifie l'équation ici, ça fait 5, 7 différentes zéros donc il n'est pas dans le grand A. Peut-être est-il dans le grand B ? Non plus. Donc, il n'est ni dans le grand A ni dans le grand B et il n'est pas dans E7. Je n'ai pas la conservation par combinaison linéaire. Je l'ai démontré. En fait, c'est juste la mathématisation de mon intuition du début que E7 n'est pas un EV. Voilà. J'espère que ça, ça vous a bien aidé. Ces deux-là, c'est un point classique. C'est bien de comprendre ça, notamment la différence intersection union. Et je vous retrouve pour une prochaine vidéo. Posez vos questions en commentaire.

Union et intersection d'EVs

RELATED

Recommended videos

Est-ce un EV ? Avec un SEV

Cas où ce n'est PAS un EV

C'est un Vect() donc un EV !