 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths
Analyse
Première

Somme de sin et cos
Ce cours aborde les exercices de mathématiques qui impliquent des sommes de sinus et de cosinus. En utilisant un cercle trigo, les valeurs des angles sont placées et les valeurs des sinus et cosinus associées peuvent être extraites rapidement. Dans l'un des exemples, les valeurs s'annulent et il ne reste que 0. Pour résoudre certains problèmes, il est important de connaître les valeurs clés de sinus et de cosinus, comme celles pour π sur 6, π sur 4, π sur 3, π sur 2, et 0. Les angles sont également présentés comme demi-racines successives dans l'ordre de leur valeur croissante. En utilisant ces connaissances sur les valeurs clés et le cercle trigo, le cours montre comment résoudre efficacement l'exercice.
Maths
Analyse
Première

Petit problème cercle trigo
Dans cet exercice de trigonométrie, on doit trouver les coordonnées de quatre points d'un carré à partir d'un point donné. Le premier point est donné par ses coordonnées, qui sont liées à la trigo, et se trouve sur le cercle de rayon 1 de centre haut, associé à l'angle pi sur 4. En utilisant la définition géométrique du carré, on peut trouver les coordonnées des autres points en observant que les diagonales se coupent en leur milieu, sont perpendiculaires et ont une même longueur. Pour trouver les coordonnées des points B et D, on ajoute plus pi sur 2 au premier angle, pour obtenir des angles de 3pi sur 4 et 7pi sur 4 respectivement. On peut ensuite lire facilement les coordonnées de ces points sur le cercle trigo en utilisant les valeurs du sinus et du cosinus. En utilisant la caractérisation du carré par ses diagonales, on peut trouver les coordonnées de tous les points du carré.
Maths
Analyse
Première

Exo bilan sur les changements de variable X=...
Dans cet exercice, on utilise une fonction contenant uniquement la variable inconnue X en termes de causes. Pour résoudre l'équation, on utilise un changement de variable en remplaçant X par X² et X. On résout ensuite les racines X1 et X2 et on les compare à la contrainte de l'intervalle de X entre -1 et 1. Ensuite, on résout F2X égale à 0 en utilisant les valeurs de X1 et X2, qui sont ensuite comparées à un deuxième inéquation pour obtenir la réponse finale.
Maths
Analyse
Première
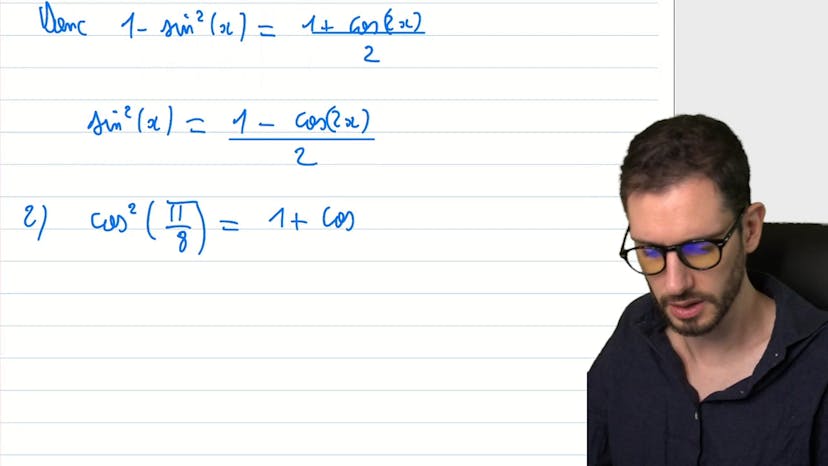
Valeur particulière d'un cos
Ce cours explique comment trouver la valeur de cos ou sin d'un réel donné en utilisant une formule admise. Pour trouver sin²x en fonction de cos²x, on utilise l'identité fondamentale de l'intrigo, sin²x + cos²x = 1. Pour trouver cosinus et sinus de pi sur 8, on utilise la formule cos²x = 1 + cos2x le tout sur 2. Ensuite, il est important de justifier pourquoi la solution positive est la bonne. En effet, pour pi sur 8, le cosinus et le sinus doivent être positifs car l'angle est compris entre 0 et pi sur 2. Enfin, il est recommandé de poser des questions dans le forum si besoin.
Maths
Probas et Stats
Première
En construction
Aucun résumé n'est disponible pour cette vidéo
Maths
Probas et Stats
Première
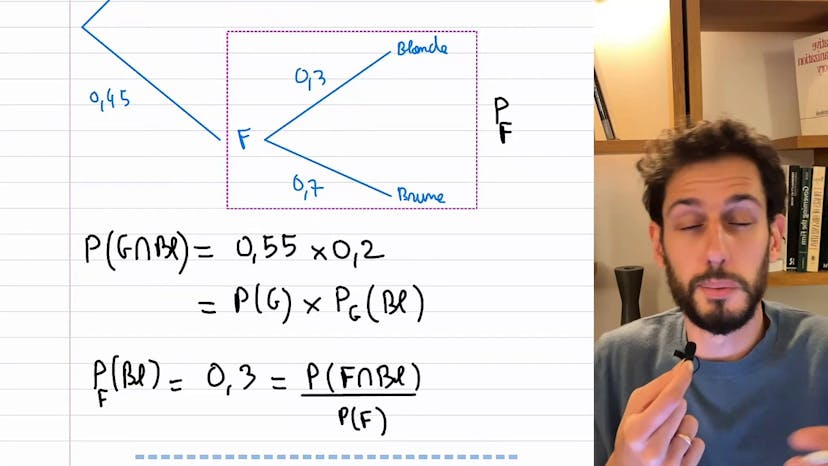
Les probabilités conditionnelles
"Pour comprendre les probabilités, il est plus simple de commencer par un exemple concret. Dans votre lycée, nous pouvons prendre l'exemple des garçons et des filles. Dans ce lycée, il y a 55% de garçons et 45% de filles. Parmi les garçons, 20% sont blonds et 80% sont bruns. Chez les filles, 30% sont blondes et 70% sont brunes. Ces statistiques nous permettent de parler de probabilités conditionnelles, qui sont les probabilités qui se produisent dans un sous-groupe. Par exemple, la probabilité d'être un garçon blond est de 0,55 x 0,2.
On peut appliquer la même logique pour les filles. En utilisant ces probabilités conditionnelles, nous pouvons calculer la probabilité d'être blond dans l'ensemble du lycée en utilisant la formule P (garçon et blond) = P(garçon) x P(blond|garçon). De la même manière, la probabilité d'être blond pour les filles est calculée avec P (fille et blond) = P(fille) x P(blond|fille). Cette formule peut également être utilisée pour calculer d'autres probabilités conditionnelles.
En résumé, les probabilités conditionnelles sont les probabilités qui se produisent dans un sous-groupe. Les exemples utilisés dans cet exemple sont les proportions de garçons et de filles blonds dans un lycée. En utilisant ces probabilités conditionnelles, il est possible de calculer la probabilité d'autres événements."
Maths
Probas et Stats
Première

Partition de l'univers
La notion de partition de l'univers est essentielle en probabilité. Une partition consiste à diviser les événements possibles en sous-ensembles distincts qui n'ont rien en commun. Par exemple, prenons l'univers des garçons, qui peut être divisé en deux catégories : les blonds et les bruns. Ceci forme une partition de l'univers des garçons car cela satisfait les deux conditions requises : tous les garçons sont inclus (20% sont blonds et 80% sont bruns) et il n'y a aucune intersection entre les deux catégories. De même, une partition peut être créée en divisant l'univers en garçons et filles, où chaque individu est soit un garçon soit une fille, et il n'y a pas d'intersection entre les deux. Une partition peut également être plus complexe, par exemple en incluant les catégories garçon-blond, garçon-brun, fille-blonde et fille-brune. En termes de probabilité, une partition est représentée par un schéma où l'univers complet est couvert, il n'y a pas de partie manquante, et les éléments des sous-ensembles sont disjoints, c'est-à-dire qu'ils n'ont rien en commun. Une partition peut être représentée mathématiquement par l'ensemble d'événements a1, a2, ..., an, où n est le nombre total d'événements et chaque événement a1, a2, ..., an représente une catégorie différente. L'ensemble des événements doit représenter 100% de l'univers et ne peut pas y avoir de chevauchement entre les événements. Une partition est un outil puissant en probabilité car elle permet de diviser l'univers en sous-ensembles distincts et complets.
Maths
Probas et Stats
Première
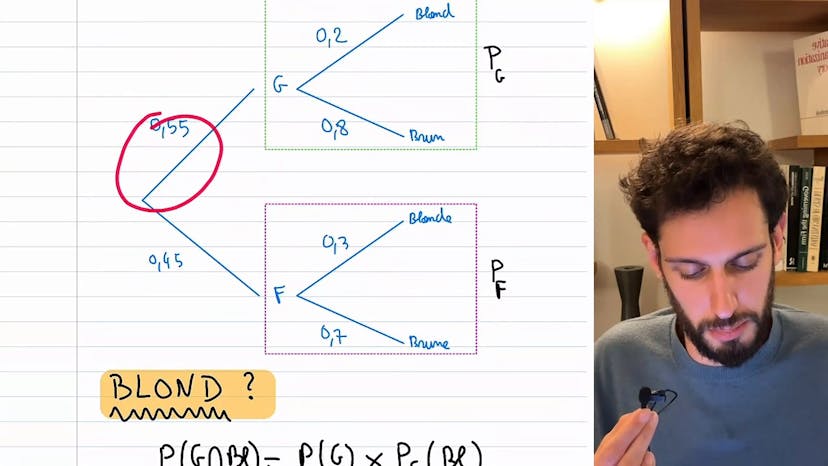
La formule des probas totales
La formule des probabilités totales est une formule très importante en statistiques. Pour l'expliquer, prenons un exemple concret d'un lycée où il y a des garçons et des filles, et des blonds et des bruns.
La probabilité d'être à la fois blond et garçon est simplement la probabilité d'être un garçon multipliée par la probabilité d'être blond (une fois qu'on a dit qu'on est un garçon).
Maintenant, intéressons-nous à la probabilité d'avoir les cheveux blonds dans ce lycée. Imaginons qu'il y ait 100 personnes : 55 garçons et 45 filles. Si je tire une personne au hasard, quelle est la probabilité qu'elle ait les cheveux blonds, qu'elle soit un garçon ou une fille ?
L'idée ici est de ne pas se focaliser uniquement sur les blonds, mais plutôt sur les deux aspects (garçon et blond). La probabilité d'être blond peut être atteinte en suivant deux chemins possibles : soit j'ai tiré un garçon blond, soit j'ai tiré une fille blonde. La formule des probabilités totales consiste à sommer ces deux probabilités pour obtenir la probabilité d'être blond.
En d'autres termes, pour trouver la probabilité que quelqu'un soit blond, je repère tous les endroits dans mon arbre qui correspondent à cet événement, c'est-à-dire être blond. Ensuite, je somme toutes les probabilités qui y conduisent.
La formule des probabilités totales peut être exprimée de deux façons : soit la somme des deux probabilités avec le signe '+', soit en utilisant la formule des probabilités conditionnelles.
En théorie, si nous avons une partition de l'univers, la probabilité d'un événement B peut être calculée en cherchant B dans chacune des branches et en les sommant toutes.
La formule des probabilités totales est donc la somme des probabilités de chaque branche contenant l'événement B. On peut également utiliser la formule des probabilités conditionnelles pour chaque élément.
L'intuition derrière cette formule est de chercher où se trouve l'événement dans chaque branche et de sommer toutes ces probabilités.
J'espère que cela a été clair pour vous. N'hésitez pas à laisser des commentaires si vous avez des questions, et à bientôt pour une prochaine vidéo. Au revoir !
Maths
Probas et Stats
Première

Indépendance
L'indépendance en probabilité est une notion essentielle. Pour comprendre cette notion, il est plus simple de comprendre la dépendance. On peut utiliser deux variables, dans cet exemple, le sexe (garçon ou fille) et la couleur de cheveux (blond ou brun). Pour chaque variable, on peut calculer les probabilités correspondantes. Si on tire un élève au hasard dans un lycée, on peut calculer la probabilité d'être blond en utilisant la formule des probabilités totales. Cependant, cette probabilité dépend du sexe de l'élève. Donc la couleur de cheveux dépend du sexe, ce sont des événements dépendants.
Pour illustrer un exemple d'événements indépendants, on peut considérer le fait d'être garçon et blond. Si la proportion de garçons blonds et de filles blondes est la même, peu importe le sexe, cela signifie que la couleur de cheveux est totalement indépendante du sexe. Dans ce cas, les deux événements sont indépendants. La définition formelle des événements indépendants est que la probabilité de l'événement B est la même que la probabilité de B sachant A.
Il est également important de comprendre les définitions formelles en mathématiques, même s'il est plus facile de les comprendre à travers des exemples concrets. Une propriété pratique des événements indépendants est que si A et B sont indépendants, alors A barre (le complémentaire de A) B est également indépendant, ainsi que A B barre et A barre B barre.
En résumé, l'indépendance des événements en probabilité signifie que la probabilité d'un événement ne dépend pas de la réalisation d'un autre événement.
Maths
Probas et Stats
Première
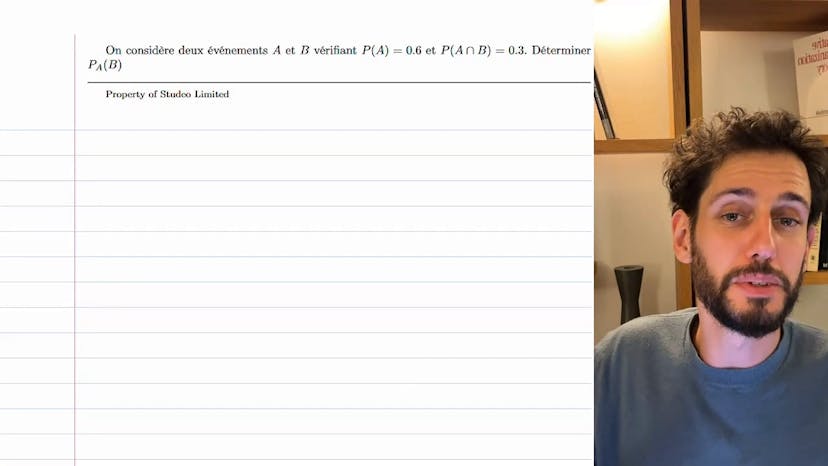
Application calculatoire
Dans ce cours, nous allons apprendre comment appliquer la formule des probabilités conditionnelles. On nous présente deux événements, A et B, et nous voulons trouver la valeur de P(B|A) en utilisant la formule des probabilités conditionnelles. Cette formule est assez simple : P(B|A) = P(A∩B) / P(A). Dans notre cas, nous avons P(A∩B) égal à 0,3 et P(A) égal à 0,6, donc P(B|A) est égal à 0,3 / 0,6, ce qui donne 1,5. On peut également représenter ces événements sous forme d'arbre avec les branches A, A' (non A), B et B' (non B) pour mieux les visualiser. Cependant, il s'agit ici de l'application la plus basique de la formule. Si vous avez des questions, n'hésitez pas à les poser avant de passer à la prochaine vidéo.
Maths
Probas et Stats
Première
Application avec contexte
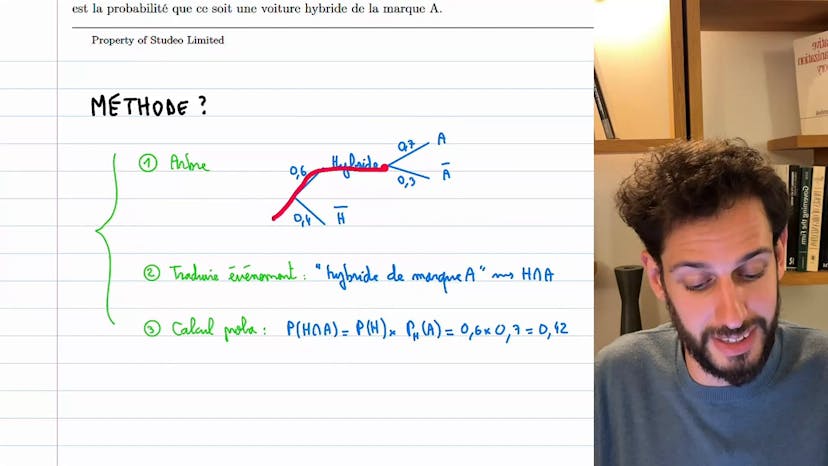
Dans cette transcription vidéo, il est question d'une application utilisant les probabilités conditionnelles. On considère une usine où 60% des voitures fabriquées sont des voitures hybrides, dont 70% sont de marque A. L'objectif est de déterminer la probabilité qu'une voiture choisie aléatoirement à la sortie de l'usine soit une voiture hybride de marque A.
Le conférencier utilise le concept d'arbre pour représenter les différentes possibilités. Il note que la première partition de l'univers est d'avoir une voiture hybride (60%) ou de ne pas en avoir (40%). Dans le sous-univers des voitures hybrides, il y a celles de marque A ainsi que d'autres marques non spécifiées.
En utilisant la formule des probabilités conditionnelles, le conférencier calcule la probabilité recherchée. Il indique que la probabilité d'avoir une voiture hybride de marque A (noté H inter A) peut être calculée en multipliant la probabilité d'avoir une voiture hybride (60%) par la probabilité d'avoir une voiture de marque A sachant qu'elle est hybride (70%, conditionnelle à H). Ainsi, la probabilité recherchée est de 0,6 * 0,7, soit 42%.
Le conférencier souligne que ce raisonnement peut sembler intuitif, mais qu'il est important de bien comprendre et appliquer les notions du cours. Il précise qu'il existe d'autres méthodes pour résoudre ce type d'exercice et invite les participants à poser des questions s'ils en ont besoin.
Dans l'ensemble, ce cours explique de manière simple et détaillée comment calculer la probabilité qu'une voiture choisie aléatoirement à la sortie d'une usine soit une voiture hybride de marque A, en utilisant les probabilités conditionnelles et en visualisant le problème à l'aide d'un arbre.
Maths
Probas et Stats
Première
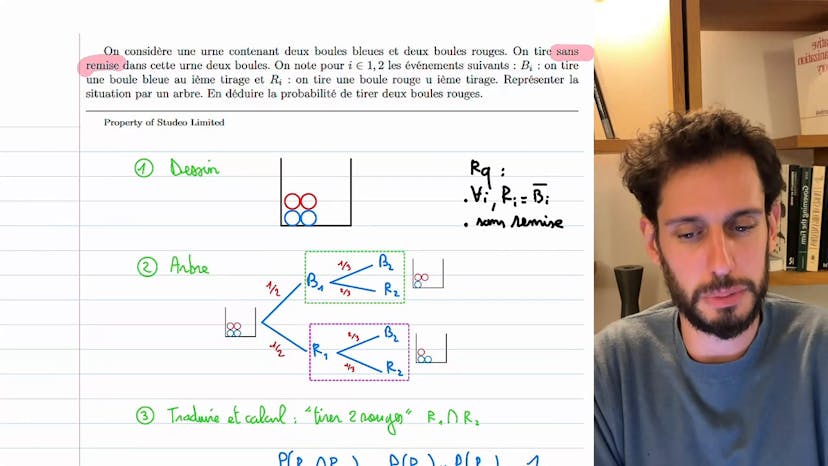
Arbre et urne sans remise
Ce cours porte sur les probabilités de tirage sans remise. L'enseignant explique qu'il est important de repérer dès le départ si on est dans le monde de sans remise ou de remise, car cela va vraiment changer la situation. Il présente un exemple avec une urne contenant des boules bleues et rouges, et explique que tirer sans remise signifie que chaque fois qu'on tire une boule, on ne la remet pas dans l'urne. Il présente également les notations bi (tirer une boule bleue au ième tirage) et ri (tirer une boule rouge), soulignant que ri est en fait le complémentaire de bi. Il utilise des dessins pour illustrer les différentes situations et sous-univers, et explique que les probabilités vont changer en fonction du nombre de boules restantes dans l'urne. Il explique ensuite comment calculer la probabilité d'avoir tiré deux boules rouges en utilisant la formule des probabilités conditionnelles. Il conclut en invitant les étudiants à poser des questions et en annonçant une prochaine vidéo.


