 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie- Physique
- Chimie
- Physique
- Chimie
TerminaleMPSI/PCSI Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie- Physique
- Chimie
- Physique
- Chimie
TerminaleMPSI/PCSI Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Physique-Chimie
Physique
Terminale

Courbe de vitesse
Dans ce cours, il est question d'une courbe de vitesse représentant le mouvement d'un point matériel. Le but est d'analyser cette courbe pour trouver différentes informations.
Tout d'abord, le mouvement est divisé en trois phases : A, B et C. Dans la phase A, la vitesse est linéaire et l'accélération est constante. Dans la phase B, la vitesse est constante et le mouvement est uniforme. Enfin, dans la phase C, la vitesse décroît de manière linéaire et l'accélération est négative.
Ensuite, on nous demande de trouver les équations horaires de la vitesse (V2t) et de la position (X2t). Pour cela, on utilise les informations de la courbe. On trouve que l'équation de la vitesse pendant la phase C est 45 - 5t.
Pour passer à l'équation de la position, on utilise le lien entre la vitesse et la position : la vitesse est la dérivée de la position par rapport au temps. En intégrant les équations horaires de la vitesse, on obtient les équations horaires de la position. Pour cela, on utilise les constantes x0 et les valeurs des phases précédentes. On trouve que l'équation de la position pendant la phase C est 45t - 5t2/2 + x0 - 92,5.
Ensuite, on nous demande de trouver les distances parcourues par le point P lors de chaque phase. On utilise les expressions des positions et on calcule la différence entre les positions extrêmes de chaque phase. On trouve que les distances parcourues sont 10m pour la phase A, 60m pour la phase B et 40m pour la phase C.
Enfin, on nous demande de calculer la distance totale parcourue par le point P. On fait simplement la somme des distances des trois phases, ce qui donne une distance totale de 110m.
En bonus, on nous demande de calculer l'aire sous la courbe de chaque phase et de faire le lien avec les distances parcourues. On remarque que les aires sous la courbe correspondent aux distances parcourues. Cela est lié à l'intégrale mathématique, qui représente l'aire sous la courbe. Ainsi, on aurait pu directement calculer les distances parcourues en regardant les aires sous la courbe.
En conclusion, ce cours permet d'analyser une courbe de vitesse et d'en tirer différentes informations sur le mouvement d'un point matériel. On utilise des notions de vitesse, d'accélération, d'équations horaires et de distance parcourue. On remarque également le lien entre l'aire sous la courbe et les distances parcourues.
Physique-Chimie
Physique
Terminale

Expérience de Milikan
Dans cette vidéo, on aborde l'expérience de Millikan, qui avait pour objectif de déterminer la charge d'un électron. Pour cela, on utilise un pulvérisateur pour créer un nuage de gouttelettes d'huile chargées négativement. On applique ensuite un champ électrique, ce qui fait que les gouttelettes tombent sous l'effet de leur poids et subissent également une force électrique. L'équilibre est atteint lorsque le poids et la force électrique se compensent.
On nous demande tout d'abord de décrire les caractéristiques de la force électrique exercée sur la gouttelette. La force électrique est donnée par l'expression F = QE, où Q représente la charge et E le champ électrique. Ici, la force électrique est verticale et dirigée vers le haut en raison de la charge négative de la gouttelette.
Ensuite, on nous demande de faire un inventaire des forces qui s'exercent sur la gouttelette. Dans ce cas, il y a uniquement la force électrique et le poids de la gouttelette.
En équilibre, l'accélération de la gouttelette est nulle, ce qui signifie que la somme des forces extérieures est nulle selon le principe d'inertie de Newton.
Pour déterminer la charge de la gouttelette, on suppose que le poids et la force électrique se compensent. On peut donc établir une relation entre les deux forces. En trouvant la masse de la gouttelette grâce à la formule M = ρV, où ρ représente la masse volumique de l'huile et V le volume lié au rayon de la gouttelette, on peut ensuite isoler la valeur absolue de la charge Q. On obtient ainsi une valeur proche de celle trouvée dans la littérature, ce qui confirme notre raisonnement.
Finalement, on nous révèle que la charge est due à un excès de 10 électrons. En faisant le calcul, on trouve une charge élémentaire proche de la valeur connue, même si on a une décimale d'écart.
En résumé, cette vidéo permet de comprendre l'expérience de Millikan et de voir comment utiliser un raisonnement mathématique simple pour déterminer la charge d'un électron.
Physique-Chimie
Physique
Terminale

Principe de Fermat
Aujourd'hui, nous allons parler du principe de Fermat en optique géométrique. Ce principe nous indique que de nombreuses lois de la physique sont basées sur la minimisation d'une grandeur. Pour comprendre ce principe, prenons l'exemple d'un sauveteur en mer. Si le sauveteur doit à la fois courir sur la plage et nager pour aller secourir quelqu'un, il doit déterminer le point de transition optimal entre la course et la nage. Si le sauveteur court trop longtemps sur la plage, il sera ralenti dans l'eau. A l'inverse, s'il entre trop tôt dans l'eau, il devra nager sur une distance trop grande. Le but est donc de trouver le point de transition optimal.
Le principe de Fermat s'applique également à la lumière. La vitesse de la lumière varie selon les milieux traversés. Ainsi, pour que la lumière se propage de manière optimale, elle doit entrer dans un milieu exactement au même endroit que le sauveteur entre dans l'eau pour sauver quelqu'un.
Pour calculer ce point de transition optimal, nous devons exprimer les différentes distances parcourues. Par exemple, la distance de course dépend de y, x et v, où y correspond à la distance sur la plage, x correspond au point d'entrée dans l'eau et v est la vitesse du sauveteur sur le sable. La distance de nage, quant à elle, dépend également de xb-x et yb, avec la vitesse αv.
Ensuite, nous devons établir la relation entre les angles I1 et I2 pour minimiser la durée du trajet du sauveteur. Pour cela, nous utilisons des notions mathématiques telles que les dérivées et les extrémums de fonctions. Par exemple, la durée totale du trajet se calcule en fonction du temps de nage et du temps de course.
En résolvant les équations, nous obtenons que sin(I1) est égal à αsin(I2). Cette relation est similaire à la loi de Descartes en optique géométrique, qui relie les angles d'incidence et de réfraction ainsi que les indices de réfraction des milieux traversés par la lumière.
En conclusion, le principe de Fermat en optique géométrique explique comment la lumière se propage de manière optimale en minimisant la durée du trajet. Ce principe est similaire au cas d'un sauveteur en mer qui doit trouver le point de transition optimal entre la course et la nage. J'espère que cette explication vous a été utile et n'hésitez pas à poser vos questions.
Physique-Chimie
Physique
Terminale
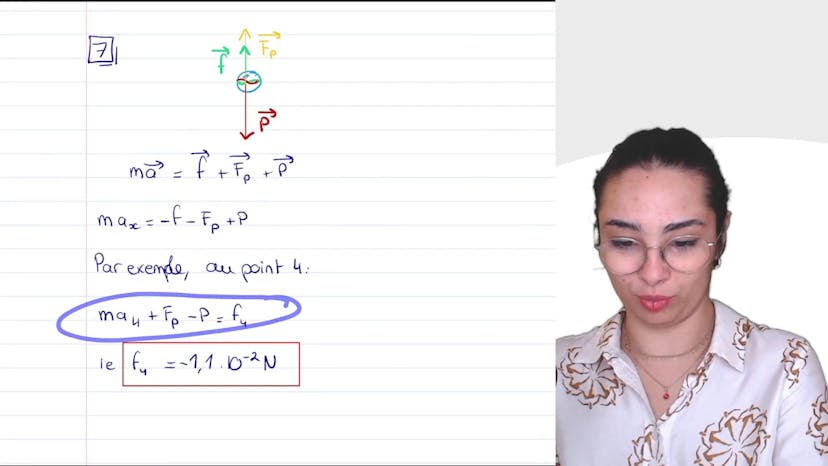
Frottements dans l’eau
Aujourd'hui, nous nous intéressons à la force de frottement lorsqu'un objet est lâché dans l'eau. Dans cet exercice expérimental, nous lâchons un objet dans un liquide de masse volumique ρ. Nous mesurons les différentes positions de l'objet à des intervalles de temps réguliers. Le frottement fluide est opposé au vecteur vitesse et proportionnel à V (la vitesse).
Nous devons calculer les vitesses en G3 et G4 en prenant deux points rapprochés et en divisant par l'intervalle de temps. La vitesse en G3 est de 2 x 10-2 m/s et celle en G4 est de 4 x 10-2 m/s. L'accélération est calculée de la même manière sur l'intervalle de temps le plus petit (0,05 secondes). L'accélération en G4 est de 4 x 10-2 m/s².
Nous devons également calculer la poussée d'Archimède. La formule est FP = ρ * V * g. La valeur de FP est donnée, nous calculons donc la valeur de la poussée d'Archimède qui est de 2,5 x 10-2 N.
Ensuite, nous calculons le poids de l'objet en utilisant la formule P = M * g. Le poids est de 3,7 x 10-2 N. Puisque le poids est plus grand que la poussée d'Archimède, l'objet va couler et non flotter.
Nous représentons les forces sur un schéma. Le poids est représenté plus grand que la poussée d'Archimède. Nous avons également représenté la force de frottement opposée au mouvement. Nous utilisons ensuite la loi de Newton (M * A = somme des forces) pour déterminer la valeur de la force de frottement. En utilisant l'accélération en G4 et les autres valeurs connues, nous trouvons une valeur de la force de frottement au point 4 de -1,1 x 10-2 N.
Nous savons que la force de frottement est proportionnelle à la vitesse. En utilisant la force de frottement au point 4 et la vitesse au point 4, nous trouvons une valeur de 27 pour le coefficient de proportionnalité.
En résumé, dans cet exercice, nous avons calculé les vitesses et l'accélération d'un objet lâché dans l'eau, ainsi que la poussée d'Archimède et le poids de l'objet. Nous avons également représenté les forces et déterminé la valeur de la force de frottement et du coefficient de frottement.
Physique-Chimie
Physique
Terminale

Chute d'un projectile
Le cours porte sur la chute d'un projectile et présente un exercice de type vrai ou faux. On nous donne une situation où un projectile est lancé d'un point O avec une vitesse initiale et un angle alpha par rapport à l'horizontale dans un champ de pesanteur uniforme G.
La première affirmation est que le vecteur accélération A du projectile ne dépend pas des conditions initiales. En appliquant le principe fondamental de la dynamique, on trouve que l'accélération est égale à G, ce qui confirme que A ne dépend pas des conditions initiales.
Ensuite, la question est de savoir si le mouvement du projectile est plan. Un mouvement est plan s'il n'est contenu que dans deux dimensions. En étudiant la vitesse du projectile, on constate que la composante selon Z est nulle, ce qui signifie que le mouvement est effectivement plan, uniquement selon les composantes X et Y.
La troisième affirmation concerne la trajectoire du projectile, on nous dit qu'elle est parabolique quelle que soit la valeur de alpha. Pour vérifier cela, on peut trouver un contre-exemple où la trajectoire n'est pas parabolique. Si on lance le projectile verticalement vers le bas, la trajectoire est rectiligne, pas une parabole. Donc, cette affirmation est fausse.
Enfin, la dernière affirmation est que pour un lancer horizontal, l'abscisse du point de chute est donnée par x = v0 * racine de (2h/g), où h est la hauteur initiale du projectile. En utilisant l'équation de la trajectoire, on trouve cette expression pour x et en l'injectant dans l'équation, on vérifie que y de x est bien égal à 0. Donc, cette affirmation est vraie.
En résumé, le vecteur accélération A du projectile ne dépend pas des conditions initiales. Le mouvement du projectile est plan, se déroulant dans les composantes X et Y. La trajectoire du projectile n'est pas toujours parabolique, sauf dans certains cas. Pour un lancer horizontal, l'abscisse du point de chute est donnée par x = v0 * racine de (2h/g).
Physique-Chimie
Physique
Terminale
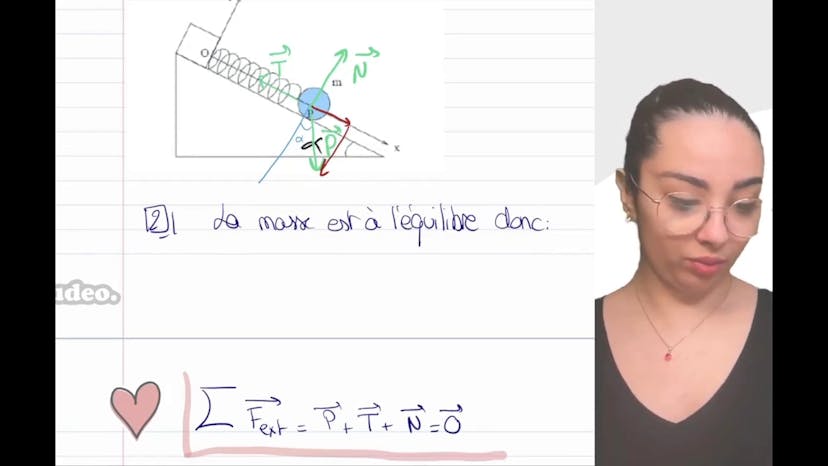
Solide et ressort
Dans ce cours, nous étudions un exercice de mécanique portant sur un solide accroché à un ressort. Le solide est à l'équilibre et se trouve sur un plan incliné. Trois forces agissent sur le solide : le poids, la tension du ressort et la réaction du support.
La première question consiste à représenter ces forces. Pour cela, il faut faire un bilan des forces, qui se compose de la force de rappel du ressort (T), du poids (P) et de la réaction du support (N).
Ensuite, nous devons calculer l'angle alpha. Pour cela, nous utilisons le fait que le système est à l'équilibre. En utilisant le principe fondamental de la statique, qui stipule que la somme des forces extérieures est nulle à l'équilibre, nous détaillons les forces. Nous projetons le poids selon les axes x et y. Sur l'axe y, nous obtenons -cos(alpha)*P et sur l'axe x, nous avons sin(alpha)*P. Nous utilisons ensuite ces projections dans l'équation de l'équilibre.
La troisième question demande de déterminer la norme de la réaction du support. Nous observons que cette réaction apparaît dans la première équation. Nous la calculons en utilisant la relation trigonométrique fondamentale : cos^2(alpha) = 1 - sin^2(alpha). En substituant cette relation dans l'expression de la réaction normale du support, nous obtenons N = P*cos(alpha) = mg*racine(1 - (T^2)/(m^2g^2)).
J'espère que cet exercice vous a été utile. N'hésitez pas à poser vos questions en commentaire.
Physique-Chimie
Physique
Terminale

Particule chargée
Aujourd'hui, nous allons étudier les particules chargées en mouvement dans un champ électrique uniforme, plus précisément entre les plaques d'un condensateur. La première étape consiste à représenter le champ électrique (E) et l'accélération (A). En utilisant le principe fondamental de la dynamique, on peut établir que mA (avec m étant la masse de la particule) est égal à la force électrique, c'est-à-dire Q (charge de la particule) multiplié par E. Si la particule est chargée positivement, la direction de l'accélération sera la même que celle du champ électrique. Ensuite, on nous demande de déterminer le signe des charges des plaques du condensateur. En général, le champ électrique va du positif vers le négatif, ce qui signifie que la plaque chargée positivement sera à gauche et la plaque chargée négativement sera à droite. La trajectoire de la particule peut également être déterminée si l'on sait que le vecteur V0 est perpendiculaire aux plaques. En utilisant les équations de base et le principe fondamental de la dynamique, on peut trouver que la trajectoire sera rectiligne uniquement dans la direction horizontale (X) et que la vitesse verticale (Y) sera nulle. Enfin, si la particule est chargée négativement, la force électrique sera dirigée dans la direction opposée à l'accélération. En utilisant les formules, on peut déduire que si la charge (Q) est positive, le VX (vitesse horizontale) sera toujours positif, tandis que si la charge est négative, le VX deviendra négatif après un certain temps. Le VY (vitesse verticale) reste inchangé. Si vous avez des questions, n'hésitez pas à les poser.
Physique-Chimie
Physique
Terminale

Champ éléctrique
Aujourd'hui, nous allons étudier le champ électrique et sa relation avec la tension entre deux plaques. Nous avons deux plaques, A et B, d'un condensateur, et un générateur de tension constant. Le champ électrique E entre les deux plaques est donné, ainsi que la distance entre les plaques. Notre objectif est de déterminer la tension UAB entre les plaques.
Pour cela, nous utilisons la formule UAB sur D = U, où U est la tension en volts et D est la distance en mètres. En substituant la valeur du champ électrique E donnée en newton par coulomb (qui est équivalente à volts par mètre), nous obtenons UAB = E x D. En effectuant le calcul numérique, nous trouvons UAB = 1 x 10^3 volts, soit des kilovolts.
Nous remarquons également que si la distance D augmente, la tension UAB augmente également, à champ électrique constant.
En résumé, ce cours porte sur la détermination de la tension entre deux plaques d'un condensateur en utilisant la formule UAB = E x D. Nous avons appris que le champ électrique est exprimé en volts par mètre et que la distance est en mètres. En augmentant la distance, la tension augmente également.
Physique-Chimie
Physique
Terminale

Accélération d’une bille
Dans ce cours, nous allons travailler sur l'accélération d'une bille soumise uniquement à la pesanteur terrestre. Le repère utilisé est OIG. La première étape consiste à déterminer le vecteur d'accélération de la bille en utilisant la deuxième loi de Newton qui stipule que la somme des forces extérieures est égale à la masse multipliée par l'accélération. Comme la bille est soumise uniquement à son poids (P = mg), on peut écrire que MA = MG, ce qui nous donne A = G. Ensuite, on nous demande les coordonnées de l'accélération dans le repère cartésien OIG. Pour cela, nous devons décomposer le vecteur G sur la base OIG. On peut observer que G est selon moins G, donc les coordonnées de l'accélération sont -G fois G. En termes de vecteurs, la première ligne représente toujours le premier vecteur de la base (I) et la deuxième ligne représente toujours le deuxième vecteur (G). N'hésitez pas à poser vos questions si nécessaire.
Physique-Chimie
Physique
Terminale

Mouvement plan
Dans ce cours, Leïla explique comment déterminer le vecteur vitesse à partir d'un vecteur d'accélération. Elle rappelle la formule d'accélération comme la dérivée de la vitesse par rapport au temps et explique qu'il faut intégrer les coordonnées une par une en prenant en compte les constantes d'intégration.
En intégrant les coordonnées selon X, Y et Z, Leïla obtient une vitesse constante selon Z et une vitesse qui varie avec le temps selon Y. Elle utilise ensuite les conditions initiales pour déterminer les constantes d'intégration.
Elle utilise les expressions données pour obtenir les coordonnées du vecteur vitesse, notées VX, VY et VZ. Ensuite, elle analyse si le mouvement est plan en vérifiant s'il se déplace uniquement dans deux dimensions.
Dans cet exemple, Leïla constate que la vitesse est nulle selon X, ce qui signifie que le mouvement ne progresse pas dans cette direction. Par conséquent, le mouvement se fait uniquement selon Y et Z, ce qui prouve qu'il est plan. Plus précisément, il est dans le plan OYZ.
N'hésitez pas à poser vos questions ou à faire part de vos remarques.
Physique-Chimie
Physique
Terminale

Masse à l’équilibre
Aujourd'hui, nous allons étudier une masse suspendue à un fil et soumise à la tension du fil ainsi qu'à son poids. L'objectif est de montrer pourquoi cette masse ne peut pas être en équilibre. Si nous examinons rapidement le problème, il semble évident qu'il s'agit d'un pendule simple. Si je déplace le pendule d'un certain angle, il reviendra à sa position initiale, il ne restera pas là tout seul. Pour expliquer cela à l'aide des lois que vous avez étudiées dans le chapitre, nous pouvons utiliser la loi de Newton, qui stipule que la somme des forces exercées doit être nulle pour être en équilibre. Dans ce cas, la somme des forces est T (la tension du fil) plus P (le poids), et cette somme n'est pas nulle, ce qui signifie que le système n'est pas en équilibre. Pour illustrer cela, nous pouvons utiliser la relation de Charles pour faire la somme des forces vectorielles. Si je déplace le poids et le place à côté de la flèche représentant la tension, la somme des forces vectorielles est représentée par le vecteur vert. Comme ce vecteur n'est pas nul, cela signifie que la masse n'est pas en équilibre. En ce qui concerne l'équilibre, si la masse passe par l'axe vertical, le poids est dirigé vers le bas et la tension vers le haut, ce qui permet d'atteindre l'équilibre. C'est pourquoi si l'on prend un pendule et qu'on le déplace, avec le temps, il reviendra à une position verticale, car c'est là qu'il atteint l'équilibre avec une somme des forces nulle. N'hésitez pas à poser vos questions en commentaire.
Physique-Chimie
Physique
Terminale
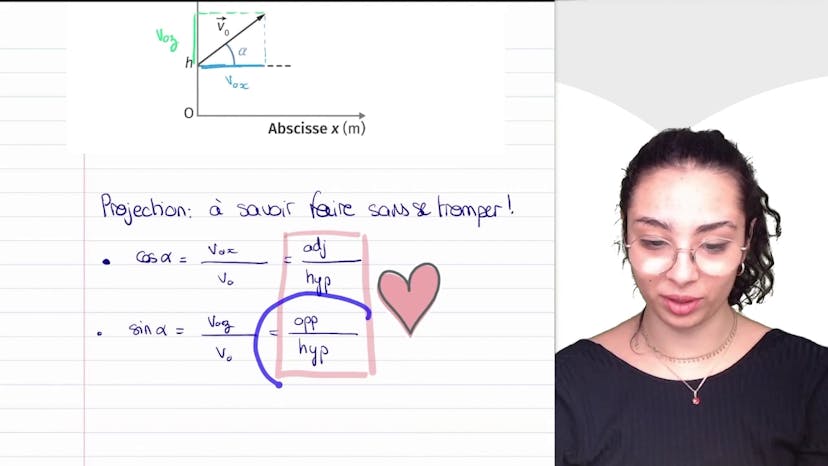
Projections
Aujourd'hui, nous allons travailler sur des projections, ce qui est important dans tous les exercices où des vecteurs sont donnés. Lorsque vous résolvez ces exercices, il est essentiel de déterminer ce qui se passe en fonction des angles. Au début, cela peut être un peu difficile car vous ne voyez pas bien où se trouvent les angles, etc. Mais nous allons le faire ensemble et vous devez garder cette technique à l'esprit. Ici, nous avons un vecteur V0 qui se décompose en composantes selon Z et X. Le but est donc de déterminer précisément les composantes selon X et Z. C'est quelque chose que vous allez trouver fréquemment dans les problèmes de mécanique. Que devons-nous faire ? Tout d'abord, nous devons regarder l'angle entre les deux. Ici, nous avons un angle avec l'horizontale appelé alpha. Dans les projections, il y a toujours des cosinus et des sinus. Avec de la pratique, vous pourrez directement identifier s'il s'agit d'un cosinus ou d'un sinus. Au début, si vous n'êtes pas sûr, je vous conseille de revenir aux formules de base. Ainsi, le cosinus d'un angle est le côté adjacent sur l'hypoténuse, tandis que le sinus d'un angle est le côté opposé sur l'hypoténuse. Il n'y a pas de tangente dans les formules de projection, car c'est toujours l'hypoténuse qui est en jeu. Je commence donc par écrire les valeurs de cos alpha et sin alpha, puis j'établis le lien avec V0x et V0y. Cos alpha est le côté adjacent sur l'hypoténuse, tandis que sin alpha est le côté opposé sur l'hypoténuse. Il ne faut pas se tromper : le côté adjacent est celui qui mène à l'angle droit, tandis que le côté opposé est de l'autre côté de l'angle droit par rapport à l'angle alpha. Une fois cela établi, j'ai une relation avec V0x, V0z, V0, cosinus et sinus. Cela me donne V0x = V0 cos alpha et V0z = V0 sin alpha. Je peux alors décomposer ces valeurs selon les vecteurs EX et EY. C'est ce qu'on appelle la projection, qui permet de déterminer les composantes selon X et Y. J'espère que cela vous a été utile, n'hésitez pas à poser vos questions.


