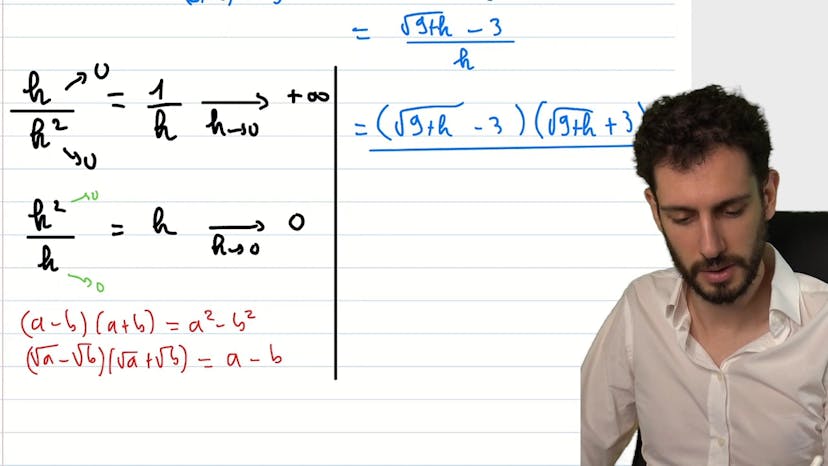Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Suites Numériques
- Second degré
- Dérivation
- Exponentielle
- Trigonométrie
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Suites Numériques
- Second degré
- Dérivation
- Exponentielle
- Trigonométrie
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
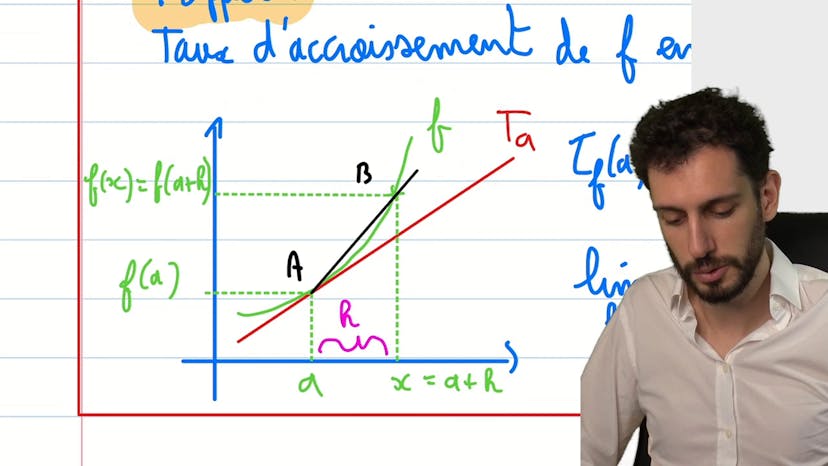
Rappel : être dérivable en un point
La vidéo explique ce qu'est être dérivable en un point. Pour être dérivable, le taux d'accroissement de la fonction en ce point doit avoir une limite finie et unique. La vidéo montre des exemples où une fonction ne respecte pas cette définition : par exemple, la fonction 1/x n'est pas définie en 0, donc pas dérivable, mais la racine de x est définie en 0 et pourtant n'est pas dérivable car elle admet une demie-tangente verticale et a une limite infinie. La valeur absolue de x est dérivable partout sauf en 0 où elle admet deux demie-tangentes de pentes opposées, ce qui ne respecte pas l'exigence d'une limite unique. Ces exemples montrent bien que la définition de la dérivabilité est importante pour comprendre et utiliser les fonctions en mathématiques.