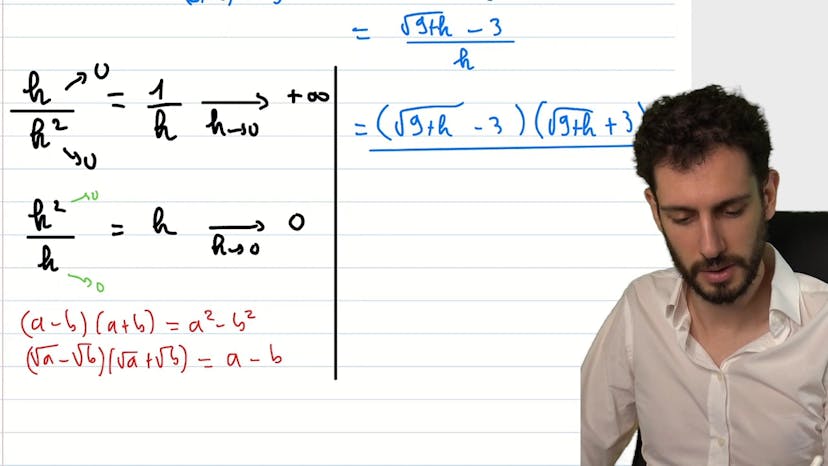Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Suites Numériques
- Second degré
- Dérivation
- Exponentielle
- Trigonométrie
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Suites Numériques
- Second degré
- Dérivation
- Exponentielle
- Trigonométrie
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
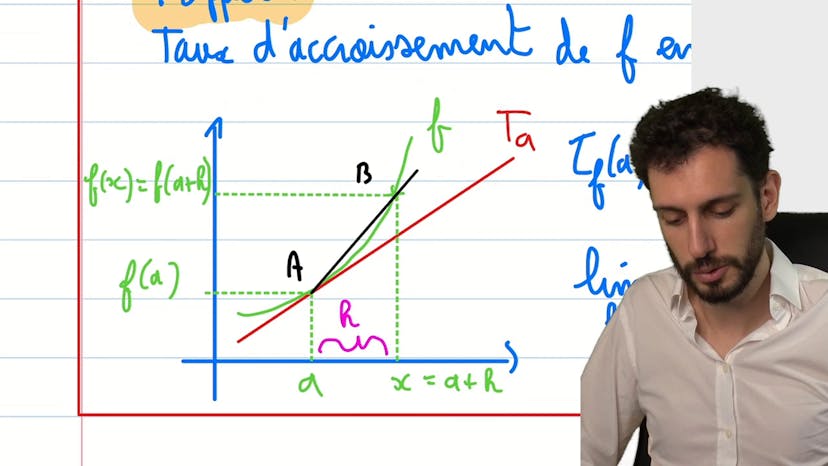
Dérivée d'une fonction
La méthode présentée ici ne vise pas à montrer la dérivabilité d'une fonction en un point spécifique, mais plutôt à comprendre quand une fonction est dérivable en général et pour quel ensemble de points, ainsi qu'à calculer la fonction dérivée associée. Il est important de retenir que les problèmes surgissent quand le contenu de la racine ou de la valeur absolue est égal à zéro, car cela entraîne une non-dérivabilité. Pour les fonctions racine et valeur absolue, les problèmes surgissent généralement lorsque le contenu est égal à zéro. Il est nécessaire de vérifier si une fonction est définie sur un ensemble et de comprendre les points où elle n'est pas dérivable. Une formule permettant de dériver une fonction de racine est présentée et doit être mémorisée. Les précautions à prendre sont de faire attention lorsque le contenu de la racine est égal à zéro, car dans ce cas, la dérivation n'est pas possible.