Approximation affine

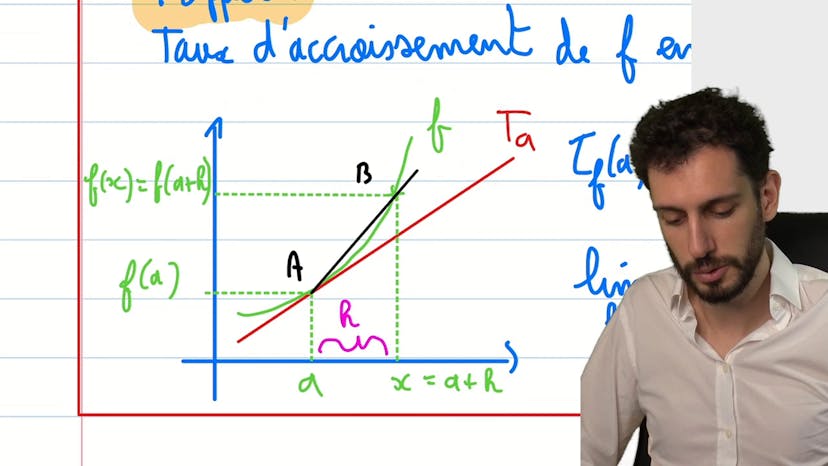
Dans ce cours sur l'approximation affine, nous examinons le concept de dérivation et expliquons comment on peut approximer une courbe en utilisant sa tangente. Tout d'abord, nous montrons que pour une fonction dérivable f, du point a à a plus h, le taux de variation est approximativement égal à f'(a). Cette formule peut être exprimée comme f(a + h) ≈ f(a) + h * f'(a). Pour mieux comprendre cette approximation, nous utilisons des graphiques. Par exemple, nous observons que lorsque nous zoomons sur une courbe, la tangente et la courbe se confondent dans une certaine plage. Nous illustrons cette idée avec différents exemples, tels que la fonction 1 + x². Ensuite, nous montrons comment cette approximation peut être utilisée pour justifier une équation particulière. Par exemple, pour la fonction f(x) = x², nous démontrons que lorsque h est proche de 0, on peut écrire 1 + h² ≈ 1 + 2h. Cette équation peut être dérivée de la formule précédente en utilisant f(1) = 1 et f'(x) = 2x. Enfin, nous utilisons cette approximation pour obtenir des valeurs approchées sans utiliser de calculatrice. Par exemple, nous approchons 1,05 et 0,999 en utilisant l'équation 1 + 2h avec h = 0,05 et h = -0,001 respectivement. Nous comparons ensuite ces valeurs approchées avec les valeurs exactes en utilisant une calculatrice. En résumé, l'approximation affine est une méthode qui permet d'approximer une courbe par sa tangente lorsque l'on se rapproche suffisamment de la courbe. Cela peut être utile pour calculer des valeurs approximatives sans avoir besoin d'une calculatrice.