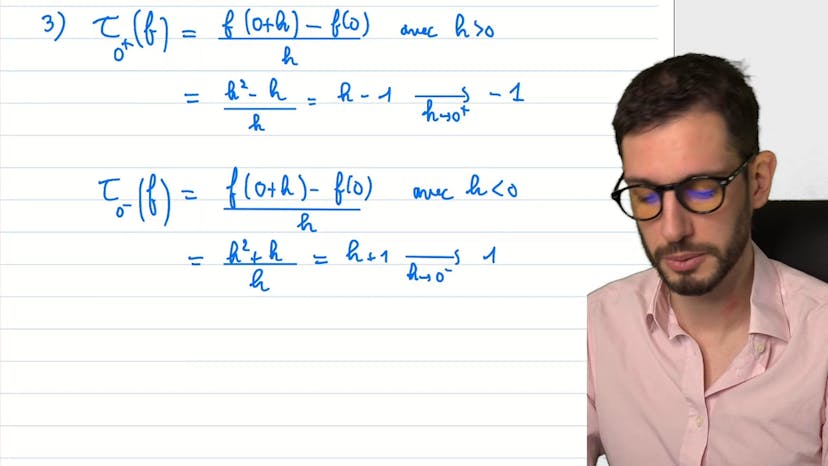Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Suites Numériques
- Second degré
- Dérivation
- Exponentielle
- Trigonométrie
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Suites Numériques
- Second degré
- Dérivation
- Exponentielle
- Trigonométrie
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Racine ET valeur absolue !
Ce cours d'analyse porte sur l'étude de la fonction f(x) qui contient une racine et une valeur absolue. On nous demande de trouver l'expression de f(x) sans valeur absolue, d'étudier sa dérivabilité et de tracer la courbe CF. Pour éliminer la valeur absolue, nous avons deux expressions à utiliser en fonction de la valeur de x. Pour étudier la dérivabilité en 1, nous trouvons deux pentes différentes, ce qui signifie que f(x) n'est pas dérivable en 1. Pour étudier les fonctions, nous dérivons f(x) en fonction de x et trouvons qu'elle est strictement croissante pour x inférieur ou égal à 1 et pour x supérieur ou égal à 5/4. Finalement, en traçant la courbe CF, nous voyons qu'il y a un point de rebroussement en 1 où la fonction n'est pas dérivable mais reste continue.