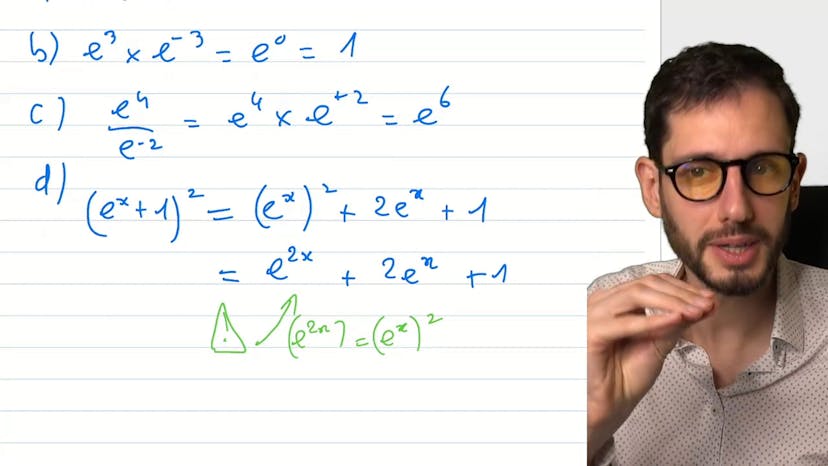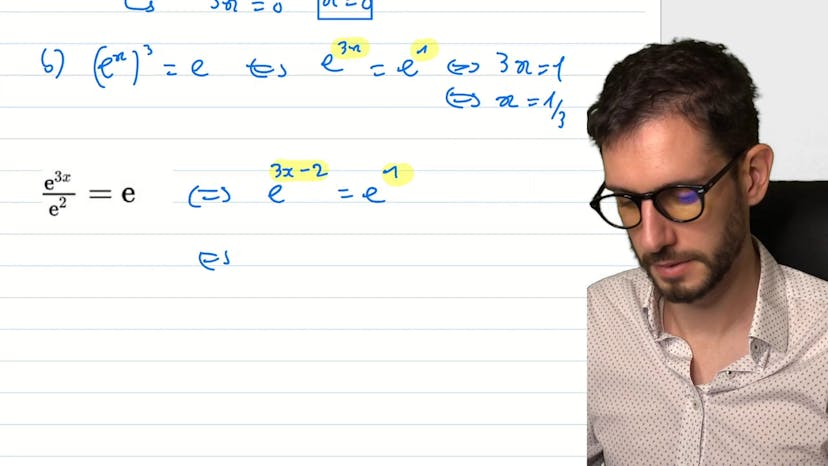Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Suites Numériques
- Second degré
- Dérivation
- Exponentielle
- Trigonométrie
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Suites Numériques
- Second degré
- Dérivation
- Exponentielle
- Trigonométrie
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Famille d'exp et leurs tangentes
Ce cours porte sur l'étude de fonctions exponentielles avec un paramètre. Nous avons une famille de fonctions fk de la forme e^(kx) - kx. Nous devons déterminer l'expression de la dérivée de fk, ce qui est assez simple puisque la dérivée de e^(kx) est k * e^(kx) - kx. Ensuite, nous devons trouver l'équation de la tangente à la courbe au point d'abscisse 0, ce qui est facile car fk'(0) = 0. L'équation de la tangente est donc y = 1. Enfin, nous devons déterminer pour quelle valeur de k la courbe fk admet une autre tangente horizontale. Nous trouvons que cela se produit lorsque k = 0 et lorsque e^(kx) = 1, c'est-à-dire lorsque x = 0. Cependant, cela correspond simplement à une fonction constante égale à 1, donc ce n'est pas très intéressant. En résumé, ce cours consiste à étudier une famille de fonctions exponentielles avec un paramètre et à déterminer les propriétés de ces fonctions, notamment leurs dérivées et les tangentes à leurs courbes.