 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Récurrence
- Limites de Suites
- Théorèmes de Convergence
- Applications avancées des suites
- Rappels sur les définitions de limites
- Rappels sur les théorèmes de convergence
- Les fondements de la continuité
- Méthodes avancées sur la continuité en un point
- Continuité sur un segment, TVI et bijection réciproque
- Généralités sur les fonctions
- Dérivation et composition : rappels
- Dérivabilité, C1 et monotonie
- Dérivée seconde et convexité
- Logarithme et puissances
- Rolle & Accroissements Finis
- Les Primitives
- Les primitives - Techniques avancées
- Les équations différentielles d’ordre 1
- Les équations différentielles d’ordre 2
- Déf&Propriétés
- Lien avec les Primitives
- Applications et Calculs
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Récurrence
- Limites de Suites
- Théorèmes de Convergence
- Applications avancées des suites
- Rappels sur les définitions de limites
- Rappels sur les théorèmes de convergence
- Les fondements de la continuité
- Méthodes avancées sur la continuité en un point
- Continuité sur un segment, TVI et bijection réciproque
- Généralités sur les fonctions
- Dérivation et composition : rappels
- Dérivabilité, C1 et monotonie
- Dérivée seconde et convexité
- Logarithme et puissances
- Rolle & Accroissements Finis
- Les Primitives
- Les primitives - Techniques avancées
- Les équations différentielles d’ordre 1
- Les équations différentielles d’ordre 2
- Déf&Propriétés
- Lien avec les Primitives
- Applications et Calculs
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths SM&SP
Analyse
2BAC SM Maroc

Variations et théorème des valeurs intermédiaires
Dans cet exercice, nous étudions le tableau de variation d'une fonction polynomiale G dont la dérivée est G'(x) = 6x² - 6x. Nous dressons le tableau en calculant les limites et en cherchant les extrêmes locaux de G.
Ensuite, nous devons montrer qu'il existe une solution alpha telle que G(alpha) = 0, avec alpha étant encadré entre -1 et 10^-1. Nous utilisons le corollaire du théorème des valeurs intermédiaires pour montrer qu'il existe une unique solution alpha sur l'intervalle (1, +∞). Nous pouvons également encadrer alpha à l'aide d'une calculatrice.
Nous déterminons ensuite le signe de G(x) pour tout x réel en utilisant le tableau de variation précédent. Ainsi, pour tout x appartenant à (-∞, alpha), G(x) est strictement inférieur ou égal à 0, et pour tout x appartenant à (alpha, +∞), G(x) est supérieur ou égal à 0.
Enfin, nous étudions la fonction f définie par f(x) = (1-x)/(x³ + 1) et nous calculons f'(x) en exprimant cette dérivée en fonction de G(x). Nous remarquons que le numérateur de f'(x) correspond à G(x), ce qui nous permet de déduire le signe de f'(x). Nous concluons que f est décroissante sur (-1, alpha) et croissante sur (alpha, +∞).
C'est ainsi que se termine cet exercice sur l'analyse de fonctions. Rendez-vous la prochaine fois !
Maths SM&SP
Analyse
2BAC SM Maroc

Point fixe et continuité
Dans cet exercice, nous cherchons à prouver que la fonction F est continue et a un point fixe sur le segment AB. Pour prouver cela, nous représentons graphiquement F dans un carré délimité par les valeurs d'A et B. Nous montrons que même en essayant d'éviter la droite identité, le graphique de F finit par l'intersecter à certains points. Ensuite, nous introduisons la fonction G(X) = F(X) - X, qui nous permet de ramener le problème à trouver une solution à l'équation G(X) = 0. En utilisant le théorème des valeurs intermédiaires, nous démontrons que l'équation G(X) = 0 a au moins une solution sur le segment AB, ce qui signifie que F(X) = X a également au moins une solution sur ce segment. Ainsi, nous prouvons l'existence d'un point fixe pour F.
Maths SM&SP
Analyse
2BAC SM Maroc
Fonction bornée
Dans cet exercice, nous étudions les fonctions continues sur un intervalle. La fonction f est définie sur R par f(x) égale à un polynôme de degrés pairs et une exponentielle de moins x carré. L'objectif est de démontrer que la fonction est bornée sur R.
Pour y parvenir, nous devons déterminer les limites de f à l'infini et moins l'infini. En utilisant les règles de calcul avec les limites, nous trouvons que la limite du polynôme est c plus l'infini et la limite de l'exponentielle est c0 plus l'infini. Les limites sont les mêmes à moins l'infini.
Selon les croissances comparées, l'exponentielle l'emporte toujours, donc les limites l'emportent sur le polynôme. Par conséquent, les limites en plus l'infini et moins l'infini de f sont 0.
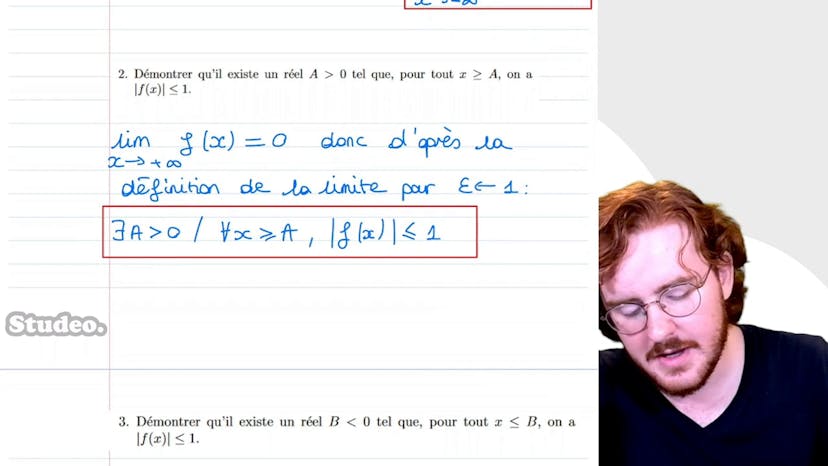
Ensuite, nous démontrons qu'il existe un réel a strictement supérieur à 0 tel que pour tout x supérieur ou égal à a, la valeur absolue de f(2x) est inférieure ou égale à 1. Cela correspond à la définition de la limite lorsque ε reçoit 1.
De manière similaire, nous démontrons qu'il existe un réel b strictement inférieur ou égal à 0 tel que pour tout x inférieur ou égal à b, la valeur absolue de f(2x) est inférieure ou égale à 1. Cette fois-ci, nous utilisons la définition de la limite en moins l'infini.
En utilisant les résultats des questions précédentes, nous remarquons que la fonction f est bornée à chaque fois sur les intervalles moins l'infini à b et a à plus l'infini. Puisque f est également continue sur l'intervalle ab, nous pouvons appliquer le théorème des bornes atteintes, ce qui signifie que f est bornée sur cet intervalle et atteint ses bornes. Par conséquent, f est bornée sur R tout entier.
Voilà, c'est la fin de cet exercice sur les fonctions continues sur un intervalle. À la prochaine fois !
Maths SM&SP
Analyse
2BAC SM Maroc

Bijection réciproque
Dans ce cours, Paul aborde le lien entre continuité, bijection et la fonction f(x) = 1 + e^x. Il montre que f est une bijection de R sur son image en utilisant le théorème de la bijection. Pour cela, il prouve que f est continue et strictement croissante en utilisant la dérivée de f. Il conclut donc que f réalise une bijection de R sur son image. Ensuite, il détermine le domaine d'arrivée de f et la bijection réciproque en résolvant l'équation f(x) = y. Il trouve que le domaine d'arrivée est R+* et que la bijection réciproque de f est f^-1 (y) = ln(e^y - 1) pour tout y dans R+*.
Maths SM&SP
Analyse
2BAC SM Maroc

Équivalent d'une bijection réciproque
Dans cette vidéo, nous étudions une fonction f définie comme f(x) = x-2 + log(x), où la fonction logarithme est définie sur l'ensemble des nombres réels positifs. Nous montrons tout d'abord que f réalise une bijection de l'ensemble des nombres réels positifs sur l'ensemble des nombres réels inclus dans R. Nous utilisons la forme explicite de f et montrons sa stricte monotonie et continuité pour prouver cette bijection. De plus, nous démontrons que l'application réciproque de f, appelée g, est également une bijection. En utilisant le théorème de limite monotone, nous déterminons les limites de g aux bornes de l'intervalle, c'est-à-dire à l'infini et moins l'infini. Nous appuyons notre démonstration sur le fait que g est strictement croissante et minorée par zéro. Nous prouvons ainsi que la limite de g à l'infini est plus l'infini et à moins l'infini est zéro. Ensuite, nous démontrons que l'équation f(x) = 0 admet une unique solution dans l'ensemble des nombres réels positifs, que nous notons alpha. Enfin, nous étudions la limite de f(x)/x et utilisons cette information pour déduire une limite pour f(g(t))/g(t) ainsi qu'un équivalent de g au voisinage de l'infini. Nous concluons la vidéo en résumant les résultats obtenus.
Maths SM&SP
Analyse
2BAC SM Maroc

Continuité et température terrestre
Dans cet exercice, Paul cherche à démontrer qu'il existe toujours deux points sur l'équateur où les températures sont égales. Il considère la température à l'équateur comme une fonction continue de la longitude.
Il explique que cette fonction, nommée T2x, est périodique avec une période de 2pi. Il montre ensuite que, graphiquement, il existe un intervalle de pi où la fonction prendra les mêmes valeurs. Il utilise le théorème des valeurs intermédiaires pour prouver cela.
Ensuite, il introduit une fonction f(x) qui est égale à T2x - T2x + pi et montre que deux valeurs de x existent, x0 et x1, telles que f(x0) est positif et f(x1) est négatif.
Il utilise ensuite la périodicité de T2x pour montrer que f(x1 +2pi) est égal à f(x1), inversant ainsi les rôles de x0 et x1. Il conclut alors qu'il existe un autre point x2 entre x0 et x1 où f(x2) est égal à zéro.
En conséquence, il démontre que pour tout point sur l'équateur, il existe un point opposé où la température est égale.
Maths SM&SP
Analyse
2BAC SM Maroc

Peu d'infos : trouver un max
Dans ce cours, on étudie une fonction continue f(x) sur R (l'ensemble des nombres réels) telle que sa limite lorsque x tend vers moins l'infini et sa limite lorsque x tend vers plus l'infini sont tous deux infinis. L'objectif est de démontrer que f admet un minimum sur R.
Nous commençons par remarquer intuitivement que si f tend vers l'infini lorsque x tend vers moins l'infini et plus l'infini, il doit exister un minimum à un certain moment, étant donné la continuité de f. Cependant, nous devons le démontrer de manière rigoureuse.
Pour ce faire, nous utilisons la propriété des limites. Nous choisissons un point a où nous appliquons les définitions des limites. Nous posons alors a = f(2,0). Grâce à cette démarche, nous pouvons trouver un nombre M1 strictement supérieur à 0 tel que si x est supérieur à M1, f(2, x) est supérieur à f(2,0) (limite en plus l'infini). De même, nous trouvons un nombre M2 strictement inférieur à 0 tel que pour tout x inférieur ou égal à M2, f(2, x) est supérieur ou égal à f(2,0) (limite en moins l'infini).
En choisissant a = f(2,0), nous savons que f(2,0) se situe entre M1 et M2. Nous avons ainsi défini notre segment [M1, M2] sur lequel f est continue et donc bornée. De plus, il existe un x0 tel que f(2, x0) soit supérieur à f(2, x0,0), ce qui signifie qu'il y a un minimum sur ce segment.
Puisque 0 appartient à [M1, M2], nous pouvons affirmer que quel que soit x en dehors de ce segment, f(2, x) est supérieur ou égal à f(2, x0,0). Ce résultat est obtenu grâce à la relation étroite étoile. Ainsi, nous sommes en mesure de dire que f(2, x) est supérieur ou égal à f(2, x0,0) sur tout R, excepté le segment [M1, M2].
En conclusion, f admet bien un minimum sur R. C'est la fin de cet exercice et à bientôt pour la suite !
Maths SM&SP
Analyse
2BAC SM Maroc
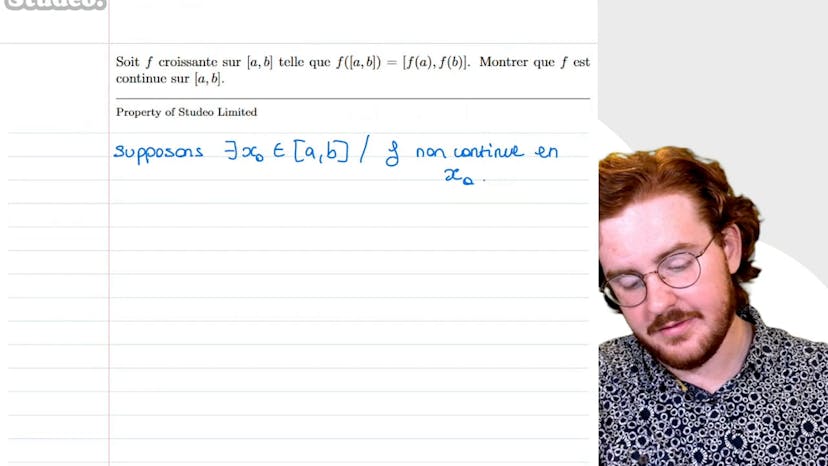
Ensemble image et continuité
Salut, dans ce cours, nous allons montrer que la fonction f est continue sur le segment AB. Pour cela, nous allons supposer par l'absurde qu'il existe un point x0 dans A et B où f n'est pas continue. Comme f est croissante et bornée sur A et B, les limites L- et L+ existent et sont finies. Si f était continue en x0, alors L- serait égal à L+. Cependant, puisque f n'est pas continue en x0, L- est différent de L+. En utilisant la croissance de f, nous pouvons montrer que pour tout x dans A et x0, f(x) est inférieur ou égal à L-. De même, pour tout x dans x0 et B, f(x) est supérieur ou égal à L+. Comme L- et L+ sont différents, il existe un alpha compris entre L- et L+ qui n'appartient pas à l'image de f sur AB. Cependant, alpha appartient à AB, ce qui crée une contradiction. Par conséquent, f est continue sur le segment AB. C'est la fin du cours, à bientôt !


