 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Physique-Chimie
Physique
MPSI/PCSI
Hauteur maximale d'une balle
Dans cette vidéo, l'exercice concerne la hauteur maximale atteinte par une balle lancée verticalement avec une vitesse initiale V0 depuis une altitude z égale à 0, en négligeant les frottements.
Il y a plusieurs manières de résoudre cet exercice. La première méthode consiste à résoudre les équations horaires en appliquant le principe fondamental de la dynamique, en dérivant et intégrant ces équations pour trouver la hauteur maximale atteinte par la balle. Cette méthode est plus longue et doit déterminer à quel instant la hauteur maximale est atteinte.
Une autre méthode plus simple consiste à appliquer le théorème énergétique. Comme le mouvement est conservatif en l'absence de frottement, cela signifie que le travail mécanique est nul (ΔEM = 0). Il faut également considérer ce qui se passe aux instants t = 0 et t = 1, car le théorème de l'énergie mécanique s'applique entre deux points précis.
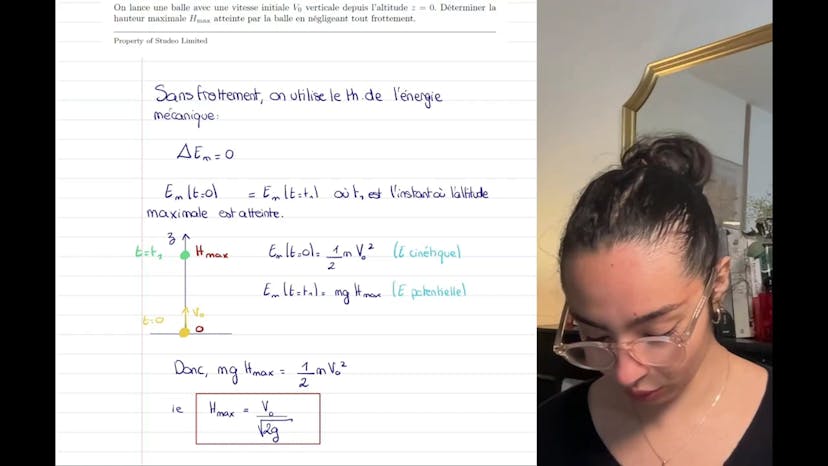
On peut donc dire que lorsque la hauteur maximale est atteinte à un instant t, il y a conservation de l'énergie mécanique entre ces deux points précis. À t = 0, la balle est lancée avec une vitesse verticale V0, ce qui signifie qu'elle possède uniquement de l'énergie cinétique verticale. À t = t1, l'énergie potentielle est maximale car la vitesse est nulle à ce moment-là.
On peut donc égaliser ces deux expressions d'énergie mécanique (EM) : EM à t = 0 est égale à 1/2MV0², et EM à t = t1 est égale à MGHmax (où G représente l'intensité du champ de pesanteur). En égalant ces expressions, on trouve Hmax = V0/√(2G), une formule couramment utilisée dans ce type de problèmes.
Ainsi, pour résoudre des exercices où l'on demande la vitesse, l'altitude ou autre en un point précis, la méthode du théorème énergétique est plus efficace que celle des équations horaires.
Au revoir à tous !
Physique-Chimie
Physique
MPSI/PCSI
Équation du mouvement d'un pendule simple
Aujourd'hui, nous allons établir l'équation du mouvement du pendule simple en utilisant les théorèmes énergétiques. Un pendule simple est un point matériel accroché à l'extrémité d'un fil tendu. Nous souhaitons exprimer l'énergie mécanique de ce pendule et justifier pourquoi elle est constante.
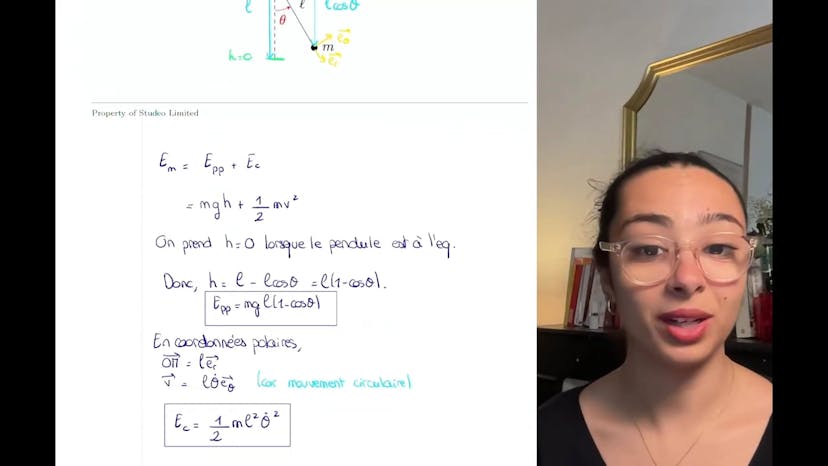
L'énergie mécanique est composée de l'énergie potentielle (Ep) et de l'énergie cinétique (Ec). Nous pouvons l'écrire comme Ep = mgh + 1,5mv², où m est la masse, g est l'accélération due à la pesanteur, h est la hauteur de la bille et v est sa vitesse. La hauteur h du pendule peut être exprimée comme h = l - lcosθ, où l est la longueur du fil et θ est l'angle que fait le pendule par rapport à la verticale.
En utilisant cette expression de la hauteur, nous pouvons retrouver l'énergie potentielle de pesanteur : Ep = mgl(1 - cosθ). Maintenant, nous avons une expression de l'énergie mécanique complète, mais nous devons également prendre en compte l'énergie cinétique.
En utilisant les coordonnées polaires, nous pouvons exprimer le vecteur vitesse de la bille (om) comme om = lθ. En dérivant ce vecteur par rapport au temps, nous obtenons l'accélération angulaire : dθ/dt = θ'. La vitesse de la bille peut donc être écrite comme Ec = 1/2ml²(θ')².
Ainsi, l'énergie mécanique totale (em) s'écrit em = mgl(1 - cosθ) + 1/2ml²(θ')². Maintenant, nous devons montrer que cette énergie est constante. Dans le cas d'un mouvement conservatif, sans frottement, nous avons em = constante.
En dérivant em par rapport au temps, nous obtenons dem/dt = mglθsinθ + 1/2ml²θ'². Pour que dem/dt soit égal à zéro (pour avoir une grandeur constante), nous devons avoir gsinθ + lθ'² = 0. Cette équation est l'équation du pendule simple.
Bien que cette méthode ne soit pas nécessairement plus rapide que le principe fondamental de la dynamique, elle permet d'utiliser une approche énergétique différente qui peut être plus simple dans certains cas.
J'espère que cela vous a été utile. N'hésitez pas à poser vos questions dans les commentaires.
Physique-Chimie
Physique
MPSI/PCSI
Energie potentielle
Aujourd'hui, nous allons parler du calcul des énergies potentielles. Le but de cet exercice est de s'entraîner à calculer ces énergies potentielles. Nous sommes donnés différentes formes d'énergie potentielle qui n'ont pas de forme physique spécifique intéressante, mais nous devons quand même calculer le gradient à chaque fois. Ensuite, on nous demande de trouver l'expression de la force associée à ces énergies potentielles. Pour cela, nous utilisons la formule F = -∇EP, qui est utilisée lorsque nous avons une force conservative. Nous pouvons ainsi déterminer l'expression de la force et de l'énergie potentielle.
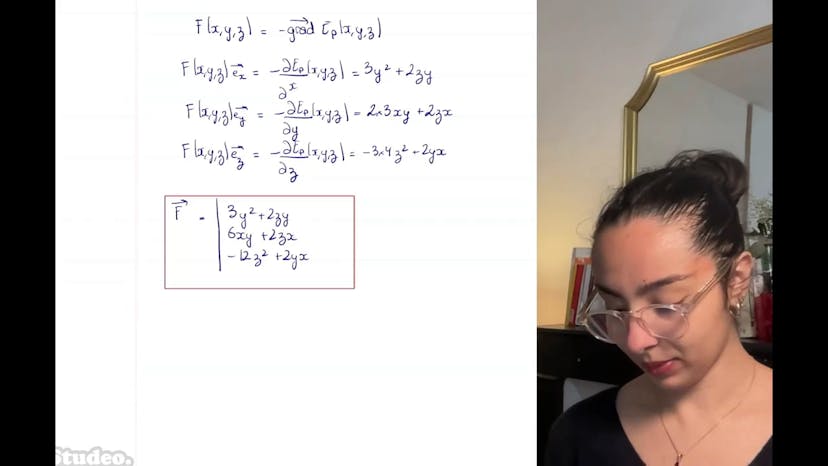
Dans cet exercice, nous commençons par calculer la force associée à une certaine énergie potentielle. Pour cela, nous projetons les effets selon chaque direction (X, Y et Z) et prenons les dérivées partielles par rapport à chaque variable. Nous obtenons ainsi les composantes de la force dans chaque direction.
Ensuite, nous faisons l'inverse : on nous donne une force et on nous demande de déterminer l'énergie potentielle associée. Dans ce cas, nous utilisons la même formule mais nous intégrons l'expression de la force pour obtenir l'énergie potentielle. Il y a une astuce dans cet exercice : nous remarquons que la force demandée est presque l'opposée de celle que nous avons calculée précédemment. Donc, nous pouvons simplement dire que la force associée à cette énergie potentielle est l'opposée de la force précédente. Nous obtenons ainsi l'expression de l'énergie potentielle.
Si nous ne remarquons pas cette astuce, nous pouvons simplement intégrer l'expression de la force par rapport à la variable correspondante. Nous obtenons ainsi l'énergie potentielle en ajoutant une constante d'intégration, qui doit être déterminée en prenant en compte les conditions initiales. Cette constante est nécessaire car l'énergie potentielle est définie à une constante près.
En résumé, cet exercice nous permet de nous entraîner au calcul des énergies potentielles. Nous calculons la force associée à une certaine énergie potentielle en utilisant le gradient, et nous calculons l'énergie potentielle associée à une certaine force en intégrant l'expression de la force.
Physique-Chimie
Physique
MPSI/PCSI
Energie potentielle d'un jeu de flèchettes
Aujourd'hui, nous allons faire un exercice sur l'énergie potentielle d'un jeu de fléchettes. Le problème est le suivant : un ressort de longueur à vide L0 égale à 10 cm est comprimé jusqu'à une longueur L1 de 4 cm. Lorsque le ressort est relâché, il permet de lancer des fléchettes d'une masse de 30 g qui atteignent une certaine altitude de 6 mètres lors d'un tir vertical. On nous donne également l'accélération de la pesanteur, qui est de 10 m/s². Notre objectif est de déterminer l'énergie mécanique totale d'une fléchette, ainsi que le niveau de référence pour l'énergie potentielle.
Pour commencer, nous pouvons faire un schéma de la situation. Le ressort est comprimé, et nous choisirons le niveau de référence pour l'énergie potentielle au niveau de l'extrémité du ressort lorsque celui-ci est comprimé. Lorsqu'il est tiré, le ressort se détend de 10 cm pour retrouver sa longueur à vide. L'énergie totale d'une fléchette est la somme de l'énergie potentielle et de l'énergie cinétique.
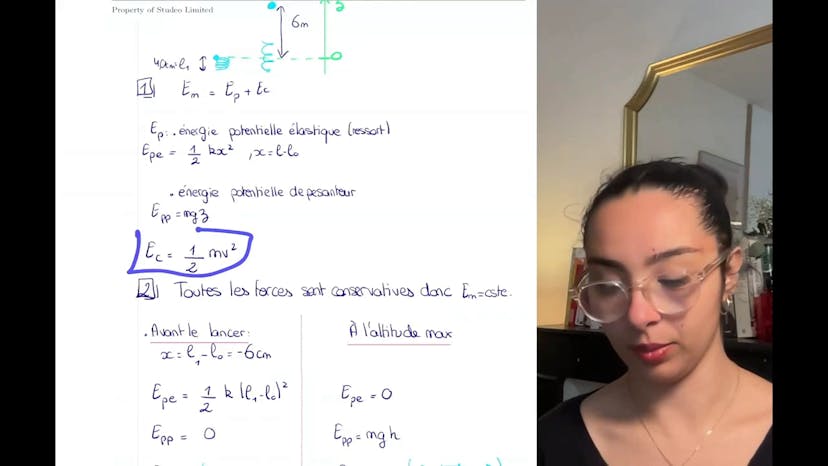
Pour calculer l'énergie potentielle élastique, qui est liée à la compression du ressort, nous utilisons la formule du cours : 1/2 * k * x², où x est la différence entre L et L0. Il y a également l'énergie potentielle de pesanteur, qui est égale à m * g * z, et l'énergie cinétique, qui est égale à 1/2 * m * v².
Pour déterminer le niveau de référence pour l'énergie potentielle, nous pouvons regarder les valeurs d'énergie potentielle de pesanteur et élastique lorsque z est égal à 0. Nous constatons que l'énergie potentielle de pesanteur est nulle, mais nous devons vérifier l'énergie potentielle élastique à ce niveau. [Note : l'orateur se trompe ici en disant que l'énergie potentielle élastique est nulle à z=0, mais cela n'a pas d'impact sur la réponse à la question posée.]
Ensuite, on nous demande de déduire la constante du ressort, K, à partir des données. Comme il y a seulement le poids et la force de rappel du ressort, l'évolution est conservative, c'est-à-dire que l'énergie mécanique est constante. Nous pouvons donc examiner ce qui se passe avant de lancer la fléchette et à l'altitude maximale.
Avant de lancer la fléchette, nous connaissons L1-L0 (soit -6 cm). L'énergie potentielle élastique est donc donnée, et l'énergie cinétique est nulle car la fléchette n'a pas encore de vitesse. À l'altitude maximale, l'énergie potentielle élastique est nulle (car le terme s'annule) et l'énergie potentielle de pesanteur est mgh. De plus, la vitesse est nulle à l'altitude maximale.
En utilisant le fait que l'énergie mécanique est constante (em1=em2), nous pouvons établir l'équation 1/2 * k * (L1-L0)² = mgh. En résolvant cette équation, nous trouvons que k = 2mgh / (L1-L0)², soit 1000 N/m avec les valeurs numériques fournies dans l'exercice.
N'oubliez pas d'inclure les unités lors de l'application numérique, sinon vous risquez d'obtenir une réponse incorrecte. J'espère que cela vous a été utile, n'hésitez pas à poser vos questions dans les commentaires.
Physique-Chimie
Physique
MPSI/PCSI
Travail d'une force
Dans cet exercice, Layla explique comment calculer le travail d'une force. Elle commence par expliquer que la force peut être modélisée par une formule générale. Elle indique qu'il est important de noter que cette force n'a pas de direction spécifique et que cela facilite le calcul.
Layla donne ensuite un exemple où un point M est déplacé d'un point A à un point B sous l'effet de cette force. Les coordonnées des points sont fournies et le but est de calculer le travail de la force.
Elle souligne que la force est constante dans le temps, ce qui rend le calcul relativement simple. Elle rappelle que le travail est donné par le produit scalaire du vecteur AB. En utilisant les coordonnées des points, elle trouve que le travail est de moins 1 joule par watt. Le signe négatif indique que la force est résistante.
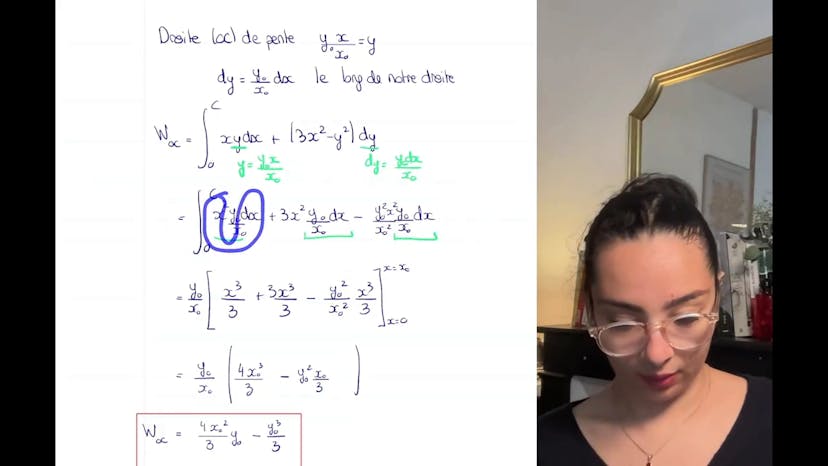
Layla donne également la formule pour calculer le vecteur AB dans un système de coordonnées donné. Dans la deuxième partie de l'exercice, elle explique que la force dépend des coordonnées x et y, ce qui signifie que sa valeur peut varier en fonction du chemin choisi.
Elle utilise alors une formule infiniment petite pour calculer le travail sur un déplacement donné. En utilisant les points 0, b, c et 0, a, c, elle calcule le travail pour deux chemins différents : passer par A ou aller directement de 0 à c.
Layla explique comment découper le calcul en deux parties en fonction des coordonnées qui varient. Pour le chemin passant par A, le travail est nul sur la partie OA, et elle obtient une expression pour la partie AC.
Pour le chemin passant par B, elle effectue le même découpage et obtient une autre expression pour le travail.
Enfin, pour le chemin direct de 0 à c, Layla détermine le vecteur directeur et explique comment éliminer une des variables pour simplifier le calcul.
Elle montre comment intégrer les expressions obtenues pour trouver le travail dans ce cas particulier. Elle conclut en expliquant que le travail dépend du chemin suivi, ce qui signifie que la force n'est pas conservative.
Layla termine en encourageant les spectateurs à poser des questions dans les commentaires et espère que cet exercice leur a été utile.
Physique-Chimie
Physique
MPSI/PCSI

Skieur
Aujourd'hui, nous allons faire un exercice de mécanique sur un skieur. Le skieur pèse 70 kg et descend une piste rectiligne inclinée d'un certain angle alpha par rapport à l'horizontale. Il est soumis à son poids ainsi qu'à la réaction de la piste, qui se divise en une composante normale et une composante tangentielle.
Tout d'abord, nous devons représenter les différentes forces sur un schéma. Le skieur est orienté vers la descente, avec son poids dirigé vers le bas et la réaction normale perpendiculaire à la piste. La composante tangentielle est dirigée dans la direction opposée au mouvement. Il est important de faire attention à ne pas confondre la réaction du support avec le frottement.
Ensuite, nous devons calculer le travail de ces trois forces pendant la descente. Le travail du poids est calculé en utilisant la formule W = ∫F.ds, où F est la force du poids projetée sur la direction du déplacement élémentaire dx. Le travail du poids est donc mg.sin(α).L, où L est la longueur de la piste. Plus l'angle alpha est grand, plus le poids travaille.
La réaction normale n'effectue aucun travail, car elle n'apporte aucun mouvement. Enfin, le travail de la force de frottement est calculé en utilisant la loi de Coulomb, qui indique que la force de frottement est égale au coefficient de frottement mu multiplié par la réaction normale. Le travail de la force de frottement est donc -mu.mg.cos(α).L, ce qui signifie qu'il est résistant au mouvement.
Ensuite, nous devons appliquer le principe de conservation de l'énergie cinétique pour déterminer la vitesse du skieur en bas de la piste. La formule utilisée est 1/2mv² = mg.sin(α).L - mu.mg.cos(α). En résolvant cette équation, nous obtenons v = racine carrée de 2gL.sin(α) - mu.cos(α), soit environ 18 m/s ou 65 km/h.
En conclusion, dans cette vidéo, nous avons appris comment calculer le travail en utilisant la formule de l'intégrale de la force scalaire du déplacement. Nous avons également utilisé le théorème de l'énergie cinétique pour calculer la vitesse en un point précis. J'espère que cela vous a été utile, n'hésitez pas à poser vos questions dans les commentaires. À bientôt !
Physique-Chimie
Physique
MPSI/PCSI
Energie potentielle de pesanteur
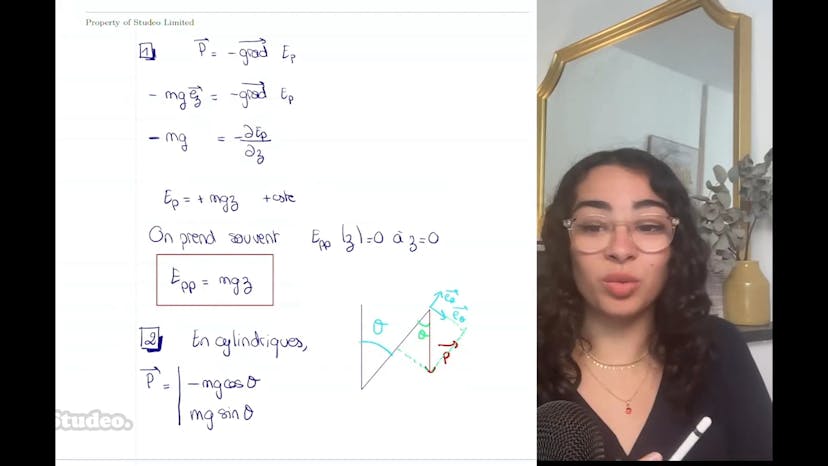
Aujourd'hui, nous allons aborder l'énergie potentielle de pesanteur dans différents systèmes de coordonnées. Dans le système cartésien, l'axe OZ est dirigé vers le haut. L'expression de l'énergie potentielle associée est donnée par EP = MgZ, où Mg représente le poids. Il est important de noter que l'expression varie selon que l'axe Z soit orienté vers le haut ou vers le bas. En coordonnées cylindriques, le poids s'exprime différemment et est donné par –Mg cosθ er – Mg sinθ eθ. L'énergie potentielle de pesanteur en coordonnées cylindriques est EP = MgR cos θ, où R représente le rayon et θ l'angle. Il est essentiel de noter que l'expression de l'énergie potentielle ne dépend que de θ en coordonnées cylindriques, et qu'elle est équivalente à celle en coordonnées cartésiennes. Les systèmes de coordonnées sont un choix arbitraire et ne doivent pas introduire de différences dans les expressions physiques. Dans notre cas, l'énergie potentielle peut être retrouvée en passant des coordonnées XYZ aux coordonnées RθZ.
Physique-Chimie
Physique
MPSI/PCSI

Mouvement sur un cercle
Dans cette vidéo, Leïla présente un exercice classique sur le mouvement d'une bille sur un cercle. L'objectif est de déterminer à quel moment la bille se détache du support. Tout d'abord, Leïla établit l'équation du mouvement en faisant un bilan des forces. Elle utilise ensuite l'énergie potentielle et le travail pour obtenir une expression en fonction de θ. Puis, elle étudie la réaction du support, qui est normale et s'annule lorsque la bille se détache. Elle montre que dans ce cas, l'énergie mécanique est constante. En utilisant la cinématique, Leïla exprime la vitesse en fonction de θ et obtient l'équation du mouvement. Elle utilise ensuite le principe fondamental de la dynamique pour trouver l'expression de la norme de la réaction du support. En simplifiant cette expression, elle détermine que la réaction est positive lorsque v0²/r est supérieur à -5g. Enfin, elle trouve l'angle θ auquel la bille se détache en isolant cosθ. Elle conclut en invitant les spectateurs à refaire l'exercice pour bien comprendre les théorèmes énergétiques.
Physique-Chimie
Physique
MPSI/PCSI
Ressorts verticaux
Aujourd'hui, nous avons abordé un exercice de mécanique et de théorème énergétique portant sur deux ressorts verticaux. Nous avons un système composé d'une masse ponctuelle accrochée à deux ressorts verticaux ayant la même constante de raideur (K) et la même longueur à vide (L0). La distance entre les points d'attache des ressorts (L) est fixe.
Nous cherchons à déterminer l'équation du mouvement en utilisant les théorèmes énergétiques. Tout d'abord, il nous est demandé de montrer que l'énergie mécanique de la masse se conserve. Pour cela, nous devons exprimer l'énergie potentielle en fonction des grandeurs du problème. La masse est soumise à deux forces conservatrices : le poids et la force de rappel des ressorts. Ainsi, l'énergie potentielle totale peut être exprimée comme la somme de l'énergie potentielle gravitationnelle (mgz) et de l'énergie potentielle élastique des ressorts (½k (z-L0)^2 et ½k (L-z-L0)^2, respectivement).
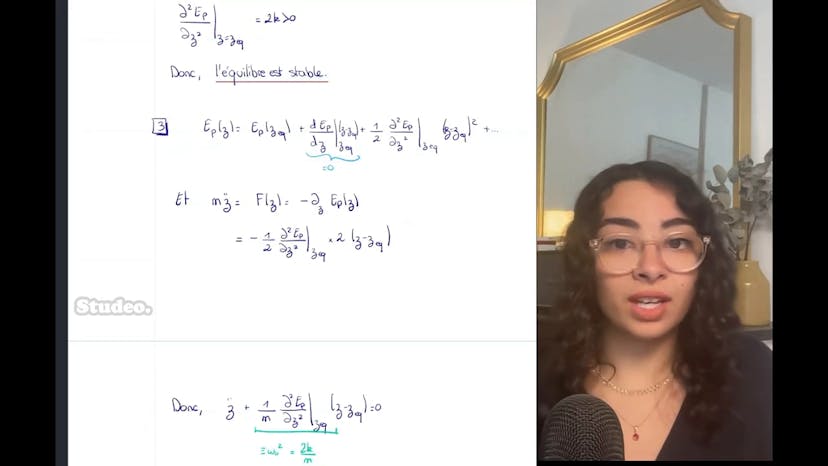
Ensuite, nous devons déterminer la position d'équilibre de la masse et discuter de sa stabilité. La position d'équilibre est l'endroit où la dérivée de l'énergie potentielle par rapport à la position s'annule. En dérivant l'énergie potentielle par rapport à z, nous trouvons que la position d'équilibre est donnée par L/2 - mg/(2k). Cette position d'équilibre est stable car la dérivée seconde de l'énergie potentielle est positive.
Nous devons ensuite déduire la période du mouvement autour de la position d'équilibre en fonction de k et m. En utilisant l'approximation des petites oscillations autour de la position d'équilibre stable, nous trouvons que la période est donnée par 2π√(m/2k).
Enfin, nous devons établir l'équation du mouvement à partir de l'énergie mécanique. En dérivant l'énergie mécanique par rapport au temps et en simplifiant les termes, nous obtenons l'équation du mouvement : mz'' = -mg + k(2z-L) où z'' est la dérivée seconde de z par rapport au temps.
En résumé, nous avons étudié les petits oscillations autour d'une position d'équilibre stable, la stabilité de cette position et l'établissement de l'équation du mouvement à partir des considérations énergétiques.


