Cours de Fonctions : Limites et continuité (1) en Ligne par les Meilleurs Professeurs - Fonctions : Limites et continuité (1)

Variations et théorème des valeurs intermédiaires

Dans cet exercice d'analyse de fonctions, l'objectif est d'être très rapide, donc il faut dresser rapidement le tableau de variation de G, qui est un polynôme, en n'oubliant pas de calculer les limites et les extrémums locaux. Ensuite, on doit déterminer l'équation de G de X égale à 0 avec X appartenant à R et donner un encadrement alpha à 10-1 près, en utilisant le corollaire du théorème des valeurs intermédiaires qui garantit l'unicité de la solution de G de X égale à 0 si on a des valeurs qui encadrent 0, ce que l'on trouve dans notre cas. On peut utiliser la calculatrice pour encadrer alpha. Ensuite, on étudie la fonction f, définie par 1 moins X sur X3 plus 1, en utilisant la dérivée f' qui est exprimée en fonction de G. En étudiant le signe du numérateur de f', qui est G de X, on peut déduire le signe de f' et les variations de f sur moins 1 plus l'infini, ce qui permet de répondre à la question 3.

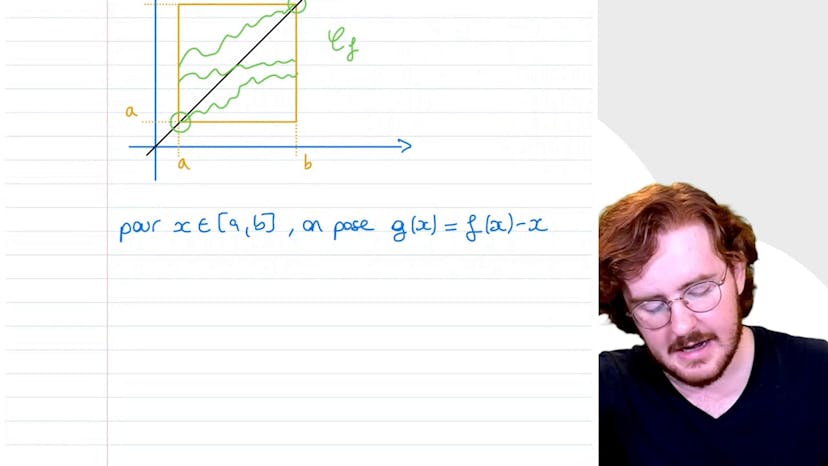
Point fixe et continuité

Dans cet exercice sur la continuité, nous prouvons que la fonction F est continue sur un segment AB et a un point fixe si elle est à valeur dans AB. En traçant un graph de F, nous montrons qu'il est impossible d'éviter la droite identité, donc F a un point fixe. Ensuite, nous posons la fonction G de X = F de X moins X pour ramener le problème en 0. Nous montrons que G est continue sur AB, et en utilisant le théorème des valences intermédiaires, nous prouvons que F de X = X a au moins une solution sur AB, donc F a au moins un point fixe.

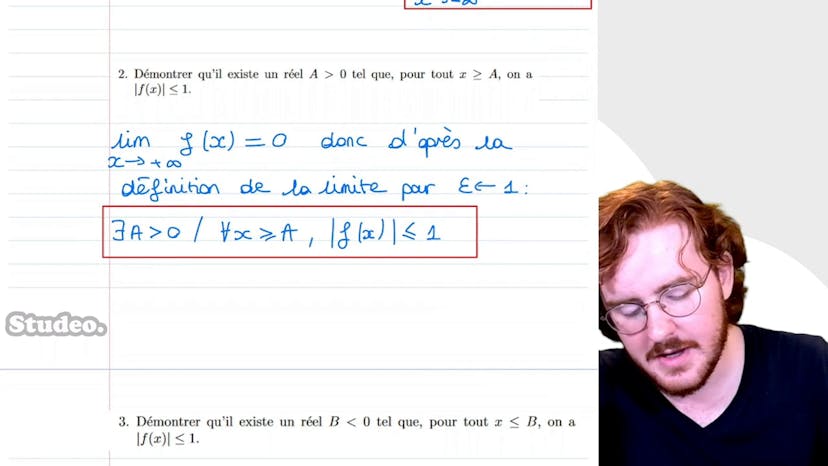
Fonction bornée

Dans cet exercice sur les fonctions continues sur un intervalle, Paul démontre que la fonction f est bornée sur R. La fonction f est définie sur R par un polynôme de degrés pairs et une exponentielle de moins x carré. Pour démontrer que f est bornée, il détermine d'abord les limites de la fonction en plus et moins l'infini en utilisant les règles de composition des limites. Puis, il démontre qu'il existe un réel a et un réel b tels que la fonction f est bornée sur l'intervalle a, b pour chaque x supérieur ou égal à a et chaque x inférieur ou égal à b. En utilisant la continuité de f sur l'intervalle a, b, il conclut que f est bornée sur R en utilisant le terme des bornes atteintes.

Bijection réciproque

Dans cette vidéo, Paul aborde le lien entre continuité, bijection et fonctions. Il considère la fonction f de x égale à 1 plus exp de x, sur le domaine R. Il montre que f est une bijection de R sur son image, en utilisant le théorème de la bijection, la continuité et la stricte croissance de f. Il détermine ensuite le domaine d'arrivée et la bijection réciproque en résolvant l'équation f de x est égal à y, et trouve que l'image de R par f est R plus étoile. Il donne l'expression de la bijection réciproque f moins 1 de y est égal à logarithm 2 exponentielle de y moins 1.

Équivalent d'une bijection réciproque

Dans cette vidéo, on étudie la fonction f définie par f(x) = x-2 + log(x) sur l'intervalle des réels positifs. On montre que f réalise une bijection de R+* dans R en montrant sa stricte croissance et sa continuité. On étudie ensuite sa bijection réciproque g, démontrant qu'elle est aussi une bijection. On prouve que la limite de g en moins l'infini est égale à zéro en utilisant le théorème de la limite monotone. On trouve également que l'équation f(x) = 0 possède une unique solution alpha dans R+*. Enfin, on détermine la limite de f(x)/x en trouvant un équivalent de g au voisinage de plus l'infini et en utilisant la composition des limites.

Continuité et température terrestre

Dans cet exercice, nous cherchons à prouver qu'il existe toujours deux points sur l'équateur ayant la même température. Pour ce faire, nous considérons la température comme une fonction continue de la longitude, T(x), qui est périodique de période 2π. Nous cherchons donc à trouver un x tel que T(2x) = T(2x+π), ce que nous traduisons en T(2x) - T(2x+π) = 0. Nous posons la fonction f(x) = T(2x) - T(2x+π), qui est continue et périodique, et cherchons deux points, x0 et x1, tels que f(x0) > 0 et f(x1) < 0. En utilisant la périodicité de T, nous trouvons x1 = x0+π tel que f(x1) = T(2x1+π) - T(2x1) = -f(x0). Nous appliquons le théorème des valeurs intermédiaires pour conclure qu'il existe un x2 sur l'équateur tel que T(2x2) = T(2x2+π), prouvant ainsi notre hypothèse initiale.

Peu d'infos : trouver un max

Dans cet exercice, Paul démontre que f, une fonction continue sur R², qui tend vers plus l'infini en moins l'infini et en plus l'infini, admet un minimum sur R. Pour trouver ce minimum, Paul applique les définitions des limites et choisit f de 0 comme valeur à analyser. Il en trouve deux valeurs, M1 et M2, et démontre que f est bornée sur leur segment commun. De plus, il montre que f de 0 est supérieur ou égal à tous les f de x, ce qui implique que f de x de 0 est un minimum de f sur R.

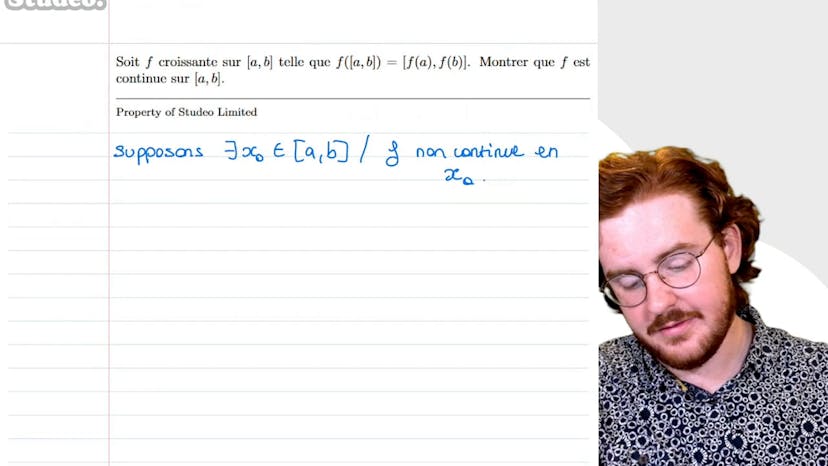
Ensemble image et continuité

Dans cet exercice de mathématiques, Paul montre comment prouver la continuité d'une fonction croissante sur un segment AB. En utilisant un dessin pour mieux visualiser, Paul illustre que la fonction croissante f doit être continue sur le segment AB pour que l'image par f du segment AB soit égale au segment f2 à f2B. Pour prouver la continuité, Paul utilise la technique de la réduction à l'absurde et montre que si f était non continue en x0, cela entraînerait une contradiction. En utilisant le théorème de la limite monotonale et les inégalités fournies par la croissance de f, Paul montre qu'il existe un alpha compris dans le segment L- L+, qui est non vide et n'appartient pas à f2 AB, ce qui contredit l'hypothèse initiale. Ainsi, f est continue sur le segment AB.

Mathématiques