 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths
Analyse
Première

Propriété fondamentale : démo
Dans ce cours, on démontre la propriété fondamentale de l'exponentiel, qui est exp de A plus B égale exp de A fois exp de B. Cette propriété ressemble à celle des fonctions de puissance. Pour démontrer cette propriété, on fixe une valeur pour B et on fait varier A pour étudier la fonction exp de A plus B divisé par exp de B. On cherche à montrer que cette fonction est égale à exp de A en montrant qu'elle vérifie les deux conditions qui définissent l'exponentiel : f' égale f et f2,0 égale 1. On utilise la fonction f2x égale exp de x plus b divisé par exp de b pour démontrer cette propriété. En vérifiant les deux conditions de définition de l'exponentiel pour cette fonction, on conclut que f2x est égale à exp de x. On peut alors déduire la propriété exponentielle en passant le exp de b de l'autre côté de l'équation. La méthode utilisée consiste à se rapporter à ce qu'on connaît sur l'exponentiel pour montrer d'autres choses, étant donné que l'on ne connaît que peu de choses sur cette fonction.
Maths
Analyse
Première
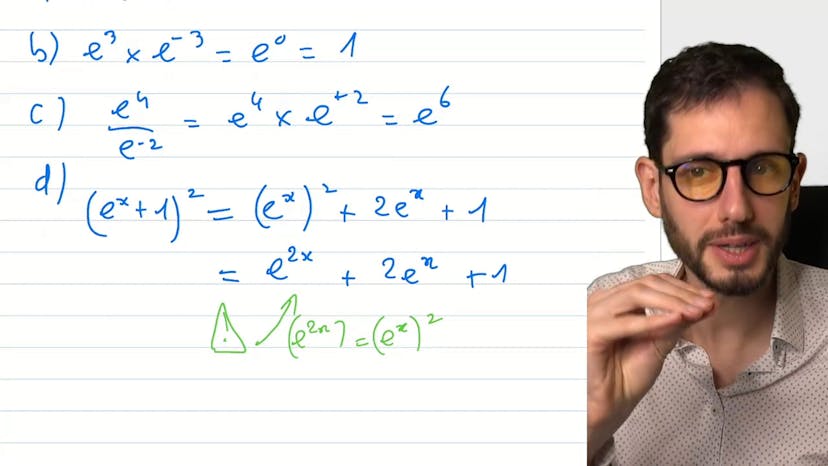
Simplifier des expressions avec exp
Dans ce cours, nous apprenons à maîtriser la simplification des expressions exponentielles. Voici quelques exemples :
- Pour l'expression E de 2 fois E de moins 1, nous simplifions en E puissance 1, soit E.
- Pour l'expression E de 3 fois E de moins 3, nous simplifions en 1.
- Pour l'expression E de 4 sur E de moins 2, nous pouvons déplacer la puissance du dénominateur au numérateur en changeant le signe, ce qui donne E de 6.
- Pour l'expression E de x plus 1 au carré, nous utilisons les identités remarquables pour développer l'expression en E de 2x plus 2 E de x plus 1.
- Nous soulignons l'importance de reconnaître que E de 2x peut être lu comme un carré, car cela peut être utile pour résoudre des équations de degré 2.
Nous notons également que E de x moins 1 multiplié par E de x plus 1 est égal à E de 2x moins 1, et que E de x moins E de moins x au carré est égal à E de 2x moins 2 fois E de x fois E de moins x plus E de moins 2x.
Il est important de pratiquer ces simplifications et de s'entraîner sur des exemples. Si vous avez des questions ou besoin d'explications supplémentaires, n'hésitez pas à me les poser. Au revoir et à bientôt pour une prochaine leçon.
Maths
Analyse
Première
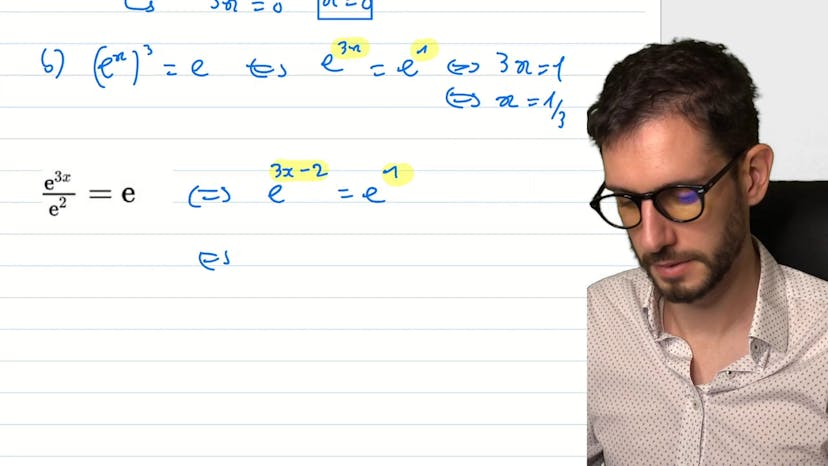
Résoudre des équations
Dans cette transcription vidéo, l'objectif est d'apprendre comment résoudre des équations en utilisant les règles de la fonction exponentielle. Différents cas sont présentés avec des exemples pratiques. Les règles à retenir sont que la fonction exponentielle est strictement croissante et qu'il n'y a pas de possibilité d'avoir deux fois la même image. Pour résoudre les équations, il est important d'identifier les puissances des expressions de chaque côté de l'équation. L'ensemble de solutions est déterminé en utilisant ces règles. Il est important de pratiquer plusieurs exemples pour acquérir la maîtrise de celles-ci.
Maths
Analyse
Première

Résoudre des INéquations
Ce cours porte sur les inéquations exponentielles. Il est important de comprendre que si la fonction est strictement croissante et que E2a est plus grand strict que E2b, alors A est plus grand strict que B. Ensuite, il est possible d'identifier des termes similaires de part et d'autre de l'inéquation et de résoudre l'inéquation. Il faut également se rappeler que la fonction E est toujours positive. Les inéquations exponentielles peuvent être résolues de la même manière que les équations, en identifiant des termes similaires.
Maths
Analyse
Première

Dériver des fonctions exp
Ce cours traite de la méthode pour calculer la dérivée d'une fonction exponentielle. La formule clé est E de u de x fois u prime de x, où u est dérivable. Si u est dérivable, cette formule est toujours vraie. Ensuite, il s'agit de pratiquer en faisant des exercices pour maîtriser la méthode. Pour les inégalités, il faut utiliser la méthode vue précédemment. Enfin, la méthode de dérivation est assez simple et nécessite juste de la pratique. La vidéo présente quelques exemples pour s'entraîner.
Maths
Analyse
Première
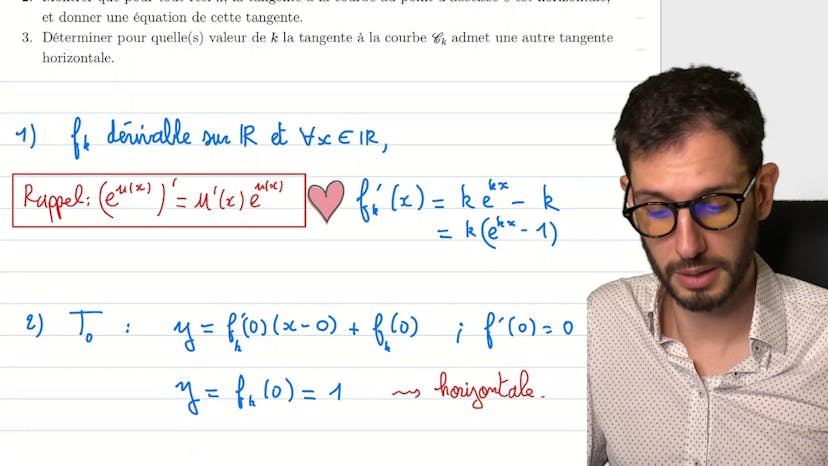
Famille d'exp et leurs tangentes
Ce cours porte sur l'étude de fonctions exponentielles avec un paramètre. Nous avons une famille de fonctions fk de la forme e^(kx) - kx. Nous devons déterminer l'expression de la dérivée de fk, ce qui est assez simple puisque la dérivée de e^(kx) est k * e^(kx) - kx. Ensuite, nous devons trouver l'équation de la tangente à la courbe au point d'abscisse 0, ce qui est facile car fk'(0) = 0. L'équation de la tangente est donc y = 1. Enfin, nous devons déterminer pour quelle valeur de k la courbe fk admet une autre tangente horizontale. Nous trouvons que cela se produit lorsque k = 0 et lorsque e^(kx) = 1, c'est-à-dire lorsque x = 0. Cependant, cela correspond simplement à une fonction constante égale à 1, donc ce n'est pas très intéressant. En résumé, ce cours consiste à étudier une famille de fonctions exponentielles avec un paramètre et à déterminer les propriétés de ces fonctions, notamment leurs dérivées et les tangentes à leurs courbes.
Maths
Analyse
Première

Fraction d'exponentielles
Ce cours aborde une méthode astucieuse pour simplifier les expressions contenant des fractions. L'idée est de faire apparaître au numérateur le dénominateur de la fraction, afin de faciliter les calculs. Pour ce faire, il est important de respecter les règles de l'arithmétique. Par exemple, en réécrivant E2x/x+3, on peut transformer cette fraction en -3/(E2x+3). Cette méthode permet de simplifier les calculs de dérivées, en concentrant les variables x au numérateur. L'expression f(x) = -6e2x/(2x+3) est ainsi dérivable et croissante. De plus, on peut démontrer que 0 < f(2x) < 2 pour tout réel x. Cette démonstration repose sur les propriétés de la fraction et permet de vérifier l'expression de base de f plus facilement.
Maths
Analyse
Première

Suite géométrique et exp
Ce cours traite des suites géométriques et de la façon de calculer leur somme. Les exercices tournent autour de la recherche de la raison de la suite et l'utilisation de la formule pour la somme d'une suite géométrique. Pour résoudre les problèmes, il faut trouver la raison de la suite et la remplacer dans la formule pour la somme. Dans le cas des exemples mentionnés, la raison était respectivement E2 et E de 0,5. En appliquant la formule pour la somme d'une suite géométrique, on peut alors trouver la solution pour la somme de ces suites. Il est important de faire attention à bien repérer où commence la suite et ne pas se tromper pour éviter toute confusion.
Maths
Analyse
Première

Etude complète de base avec exp
Ce cours porte sur l'étude d'une fonction exponentielle et un peu d'X. La question 1 est importante car elle révèle une fonction impaire, ce qui implique une symétrie centrale. Une astuce consiste à simplifier l'expression pour une meilleure compréhension. La méthode la plus rapide consiste à étudier la variation de la fonction en trouvant sa dérivée. On peut étudier la position relative de la fonction par rapport à une droite donnée en comparant leur différence. Enfin, on peut étudier la fonction pour des valeurs négatives et positives en approchant zéro ou l'infini.
Maths
Analyse
Première
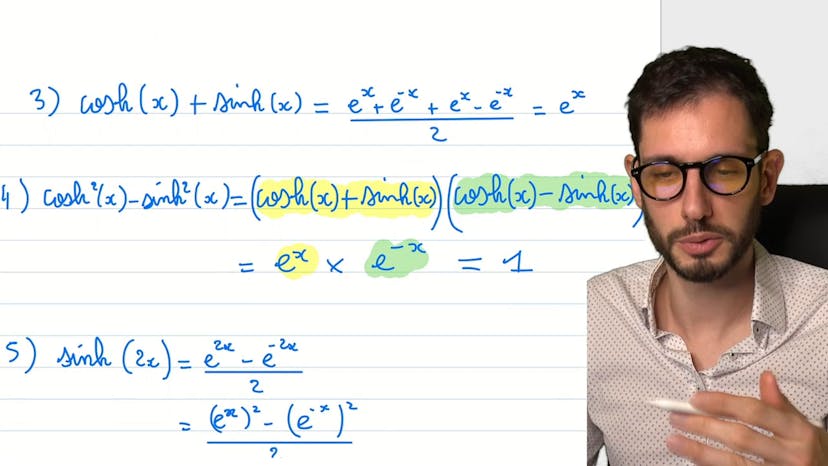
Cos et Sin hyperboliques !
Dans ce cours, nous étudions les fonctions cosinus et sinus hyperboliques, qui sont des fonctions courantes en physique et en maths pures de première année. Nous démontrons que cosinus hyperbolique (cosh) est pair et nous étudions ses variations sur l'intervalle 0 plus infini. Nous faisons de même pour le sinus hyperbolique (sinh). Nous étudions également quelques relations intéressantes entre les fonctions, telles que cosh plus sinh et cos² moins sin². Enfin, nous démontrons que deux fois le sinus hyperbolique de 2X est égal à la multiplication de cosinus hyperbolique et sinus hyperbolique de X.
Maths
Analyse
Première

Dérivabilité en 0 (1er exemple)
Dans cet exercice de mathématiques, on étudie la dérivabilité d'une fonction définie en deux parties. Tout d'abord, pour les valeurs différentes de 0, cette fonction est égale à l'expression e^(1/x) où x est non nul et positive. Ensuite, on ajoute la valeur f(0) = 0 à cette fonction pour l'étendre sur l'ensemble des réels. Pour étudier sa dérivabilité, on utilise deux méthodes. La première méthode est la méthode classique qui consiste à étudier un taux d'accroissement de la fonction en 0. On obtient ainsi que la fonction n'est pas dérivable en 0 car le taux d'accroissement admet une limite infinie. La seconde méthode utilise le graphique de la fonction pour montrer qu'elle n'est pas continue. Par conséquent, elle n'est pas dérivable. Deux méthodes simples pour étudier la dérivabilité d'une fonction mathématique en utilisant des concepts telles que les taux d'accroissement et la continuité de la fonction.
Maths
Analyse
Première
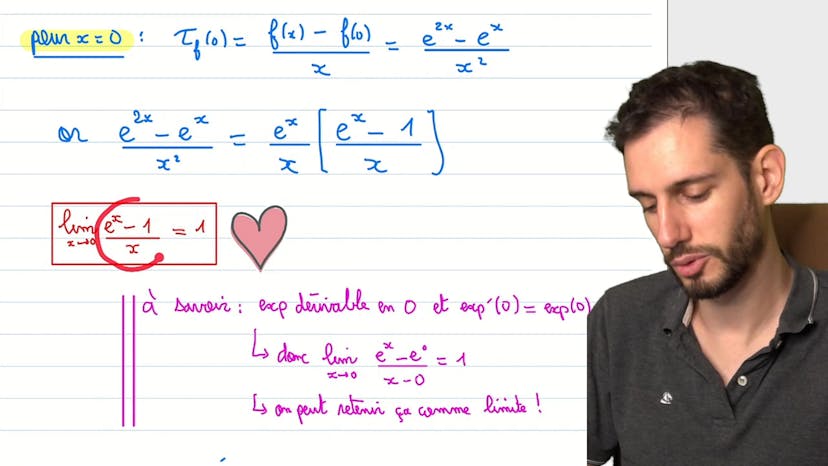
Dérivabilité en 0 (2ème exemple)
Dans cet exercice, on doit étudier la dérivabilité d'une fonction comprenant de l'exponentiel pour une valeur donnée en 0. La méthode consiste à calculer le taux d'accroissement en ce point et vérifier s'il admet une limite finie. On factorise ensuite le taux d'accroissement pour faire apparaître le ratio e2x-1 sur x, qui a une limite de 1 lorsque x tend vers 0. Cette limite est la définition de la dérivabilité de la fonction exponentielle en 0. En utilisant cela, on peut simplifier l'exercice et conclure que la fonction n'est pas dérivable en 0 car son taux d'accroissement tend vers plus ou moins l'infini en ce point.
Maths
Analyse
Première

Dériver 2 fois pour conclure !
Nous étudions une fonction complexe et examinons la méthode d'étude de fonction. Nous commençons par vérifier si la fonction est paire ou impaire, puis si elle est trivialement croissante ou décroissante. Ensuite, nous examinons la dérivée et étudions le signe de l'expression pour en déduire le signe de la fonction. Si nous ne pouvons pas simplifier l'expression de la dérivée, nous pouvons étudier la fonction elle-même pour en déduire son signe. Nous pouvons redériver la fonction pour avoir sa dérivée seconde et trouver les points de minimums ou maximums en cherchant ses racines. En utilisant cette méthode, nous pouvons résoudre des fonctions complexes et obtenir de meilleurs résultats aux contrôles.
Maths
Analyse
Première
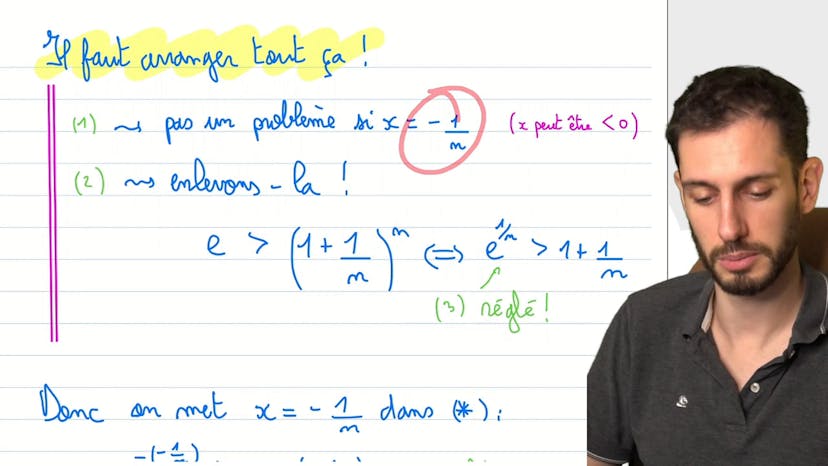
Encadrement de e par des suites
Cette transcription d'une vidéo explique comment trouver un encadrement de la constante E de l'Eve à partir d'un exercice en combinant l'exponentiel et la suite. Les deux premières questions portent sur le comportement de l'exponentiel par rapport à X, tandis que les questions suivantes impliquent des applications d'entiers et l'étude de suites. À la question 5, on doit montrer une inégalité avec de l'exponentiel et du X en utilisant une fonction. Enfin, à la question 6, on doit trouver un encadrement de E avec une amplitude de 10^-6 en utilisant les résultats des questions précédentes. Pour cela, on utilise une valeur de N telle que l'écart entre deux valeurs encadrant E est inférieur à 10^-6. Il est important de suivre la méthode étape par étape et de ne pas paniquer.


