 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths Expertes
Arithmétique
Terminale

Déterminer un PGCD
Dans cet exercice, on apprend à calculer le PGCD de deux nombres: 18 840 et 9828. La méthode la plus simple est l'algorithme d'Euclide, qui utilise des divisions euclidiennes successives. On commence par diviser le plus grand nombre par le plus petit. Ensuite, on continue à diviser le diviseur par le reste jusqu'à obtenir un reste de 0. Le PGCD est alors le dernier reste non nul. Dans ce cas, le PGCD de 18 840 et 9828 est 12.
Maths Expertes
Arithmétique
Terminale

Différence et quotient
Dans cet exercice, on doit trouver deux nombres entiers dont la différence est égale à 538. On sait également que lorsqu'on divise l'un par l'autre, le quotient est 13 et le reste est 34. On note ces deux nombres A et B, et on suppose que A est plus grand que B. On écrit deux équations pour ces informations et on résout le système : A-B=538 et A=13B+34. On trouve B=42, ce qui nous permet ensuite de trouver A=580.
Maths Expertes
Arithmétique
Terminale
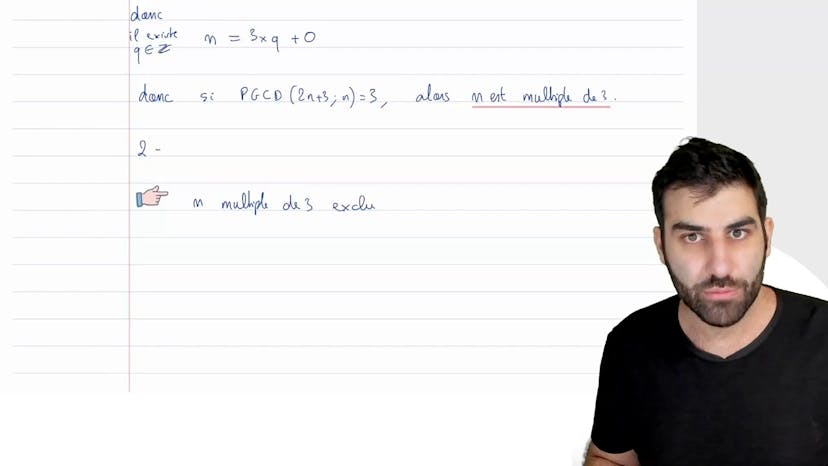
PGCD qui dépend de n
Dans cet exercice, on cherche à déterminer l'ensemble des entiers naturels n permettant que le PGCD de 2n+3 et de n soit égal à 3. En effectuant la division euclidienne de 2n+3 par n, on trouve que si le PGCD est égal à 3, alors n est divisible par 3. Ensuite, si l'on cherche à déduire l'ensemble des entiers n pour lesquels le PGCD de 2n+3 et de n est égal à 1, on remarque que lorsque n est multiple de 3, le PGCD ne peut pas être égal à 1. Ainsi, si n est de la forme 3k+2 ou 3k+1, où k est un entier naturel, alors le PGCD est égal à 1.
Maths Expertes
Arithmétique
Terminale

Autre dépendance en n
Dans cet exercice, on cherche le PGCD de deux entiers A et B qui dépendent de n. On commence par éliminer n en faisant une combinaison linéaire de A et B. On trouve que le PGCD divise 5, ce qui nous permet de réduire les possibilités à 1 ou 5. On étudie ensuite chaque cas : si le PGCD est 5, n doit être congru à 1 modulo 5, sinon, le PGCD est 1.
Maths Expertes
Arithmétique
Terminale
PGCD et n carré
Aucun résumé n'est disponible pour cette vidéo
Maths Expertes
Arithmétique
Terminale

PGCD et PPCM
Dans cet exercice, on doit trouver deux nombres et manipuler le PGCD et le PPCM. On sait que A est plus petit que B, leur PGCD vaut 6 et leur PPCM vaut 102. En utilisant une formule qui relie le produit de deux nombres au produit de leur PGCD et PPCM, on peut trouver A' et B' tels que A est 6 fois A' et B est 6 fois B', et A' et B' sont premiers entre eux. En simplifiant cette formule, on obtient A'B' est égal à 17, donc A' vaut 1 et B' vaut 17. A est donc 6 et B est 102.
Maths Expertes
Arithmétique
Terminale

PGCD et congruences
Dans cet exercice de mathématiques, nous manipulons le PGCD et des congruences. Le système S établit que n est congruent à 1 modulo 5 et à 5 modulo 7. Nous devons montrer que si n vérifie le système S, alors il vérifie également un autre système. Nous montrons cela en utilisant des congruences et en utilisant le corollaire du théorème de Gauss. Nous en déduisons que 4n est congruent à moins 1 modulo 35, et en résolvant cette équation, nous obtenons que l'ensemble des solutions est {26 + 35k | k ∈ Z}.
Maths Expertes
Arithmétique
Terminale

PGCD et Suite
Dans cet article, nous étudions un exercice sur le PGCD et les suites. Nous avons une suite définie sur n, avec u0 = 0 et u1 = 1, et une relation de récurrence. Nous avons également une autre suite, vn, définie comme étant un + 1 - un. Nous montrons que vn est une suite géométrique de raison 2 et que le terme initial v0 est égal à 1. Nous déduisons ensuite que pour tout entier n, un est un entier naturel et que un + 1 est égal à 2 fois un + 1. Nous utilisons ensuite une somme télescopique pour montrer que un est un entier. Enfin, nous utilisons le théorème de Bézout pour montrer que deux termes consécutifs de la suite sont premiers entre eux.
Maths Expertes
Arithmétique
Terminale
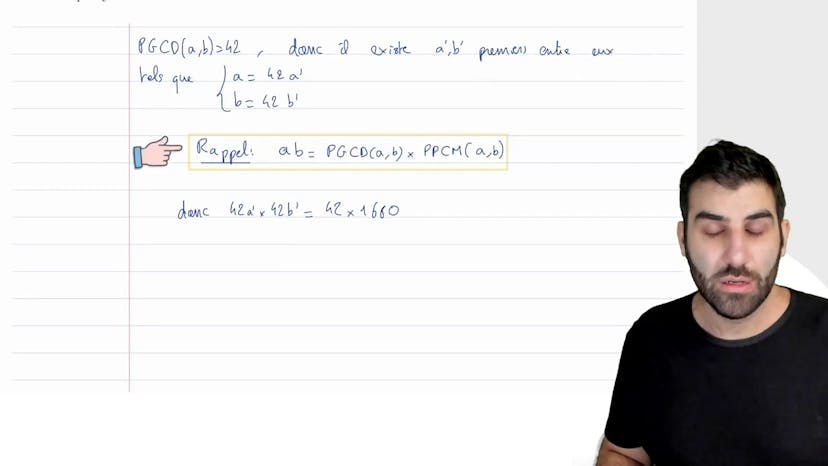
PGCD+PPCM
Dans cet exercice, on cherche un couple A et B qui ont un PGCD de 42 et un PPCM de 1680. On utilise une méthode où l'on extrait des diviseurs premiers de A et de B qui sont premiers entre eux, puis on simplifie l'équation en utilisant une formule qui relie le PGCD et le PPCM. Après simplification, on obtient que A'B' est égal à 40, et en excluant les diviseurs de 40 qui ne sont pas premiers entre eux, on obtient les deux possibilités suivantes : A est égal à 42 et B est égal à 1680 ou A est égal à 210 et B est égal à 336. Ces sont toutes les solutions du système d'équations avec le PGCD et le PPCM.


