 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens- Concours et examens UK
- Oxford Imperial MAT
- Cambridge
- Concours et examens US
- Concours et examens Français
- Bac et examens étrangers
Terminale
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens- Concours et examens UK
- Oxford Imperial MAT
- Cambridge
- Concours et examens US
- Concours et examens Français
- Bac et examens étrangers
Terminale
Prépa Examens
Concours et examens UK
Terminale

n réels et n équations circulaires !
Bonjour à tous,
Aujourd'hui, nous allons résumer une transcription d'une vidéo portant sur un exercice de mathématiques tombé à Cambridge en 1999. L'exercice consiste à trouver les valeurs des nombres positifs x1 à xn qui satisfont certaines conditions.
L'intérêt de cet exercice réside dans sa simplicité, car il ne nécessite pas de grandes connaissances mathématiques. Il s'agit principalement d'une question de logique et de raisonnement.
La première partie de l'exercice consiste à montrer que chaque nombre est plus grand que 1. En utilisant les définitions des nombres fournis dans l'énoncé, cette partie est assez simple à résoudre.
Ensuite, l'exercice demande de montrer que tous les nombres sont égaux. Pour cela, l'auteur utilise les résultats obtenus dans les parties précédentes. Il effectue plusieurs remplacements et parvient à montrer que tous les nombres sont égaux à x1.
Enfin, l'exercice demande de trouver la valeur de x1. En résolvant une équation du second degré, l'auteur trouve deux solutions, dont une qui correspond à la valeur de x1.
En conclusion, tous les nombres positifs x1 à xn sont égaux à 1 plus la racine de 5 divisée par 2.
Cet exercice nécessite de la réflexion et du raisonnement, ainsi qu'une bonne compréhension des différentes étapes. Il est important de ne pas négliger les détails pour éviter les erreurs. Si vous avez des questions ou si vous avez trouvé une autre démonstration, n'hésitez pas à les partager.
À bientôt dans une prochaine vidéo !
Prépa Examens
Concours et examens UK
Terminale
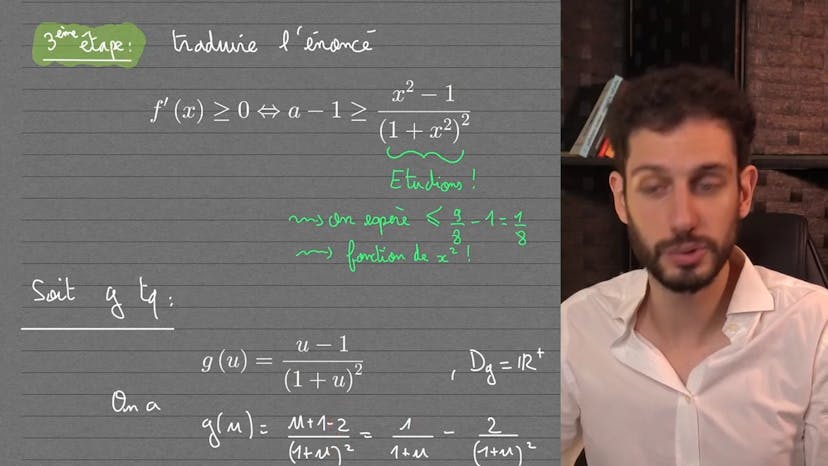
Une fonction musclée !
Dans cette vidéo, l'exercice proposé concerne une fonction f'x égale à ax-x³ sur 1 plus x². L'objectif est de démontrer que si a est supérieur ou égal à 9 huitièmes, alors f'x est toujours positif. Pour cela, le professeur utilise une méthode de simplification des fractions avec des polynômes en haut et en bas, pour ensuite dériver et exprimer la condition recherchée. Il utilise également un changement de variable pour simplifier les calculs. Finalement, en étudiant une autre fonction et en montrant qu'elle est inférieure à un huitième, il démontre que si a est plus grand ou égal à 9 huitièmes, alors f'x est positif ou nul. L'exercice nécessite une bonne maîtrise des techniques mathématiques et de l'indépendance dans l'approche des problèmes.
Prépa Examens
Concours et examens UK
Terminale

Résoudre x = aˣ, et en moins de 10 minutes
Bonjour à tous ! Aujourd'hui, je vais résumer en utilisant des termes SEO-friendly un cours qui est une transcription d'une vidéo. Dans ce cours, nous allons aborder un exercice qui est tombé à Cambridge en 2014. Cet exercice ressemble à un exercice d'analyse de fonctions qui peut être réalisé en Terminale, grâce aux outils que nous utilisons régulièrement. L'énoncé nous demande de démontrer que l'équation x égale a puissance x n'a aucune racine réelle si a est strictement supérieur à e puissance 1 sur e. Nous supposons que a est positif pour simplifier les calculs. Ensuite, nous déduisons que x doit également être positif pour éviter une contradiction. Pour résoudre cette équation, nous prenons le log de chaque côté pour simplifier les calculs. En dérivant, nous étudions les variations de la fonction f et trouvons son maximum. En analysant les limites de la fonction, nous déterminons les conditions pour lesquelles elle a des racines réelles ou non. Finalement, nous concluons que si a est strictement supérieur à e puissance 1 sur e, l'équation n'a pas de racines réelles, et si a est strictement inférieur à 1, l'équation a une unique racine réelle. J'espère que cette résumé SEO-friendly vous a aidé à comprendre le contenu du cours. N'hésitez pas à vous abonner à la chaîne pour plus de vidéos et de conseils mathématiques. À bientôt !
Prépa Examens
Concours et examens UK
Terminale

Des puissances 100 et plus ?
Dans cet exercice, on nous donne une suite récurrente définie par a1 = 3 et an+1 = an^3 pour n ≥ 1. On nous demande de trouver le chiffre des unités pour le nombre a7, de montrer que a7 ≥ 10^100, et de déterminer la valeur de (a7 + 1) / (2a7) avec une précision de deux décimales.
Pour la première question, on analyse la suite et on remarque que les chiffres des unités alternent entre 7 pour les indices pairs et 3 pour les indices impairs. Donc le chiffre des unités pour a7 est 3.
Pour la deuxième question, on utilise la formule explicite de an = 3^n-1 et on montre que a7 = 3^(3^6) qui est beaucoup plus grand que 10^100. Donc a7 ≥ 10^100.
Pour la troisième question, on écrit (a7 + 1) / (2a7) = 1/2 + 1/(2a7) et on constate que 1/(2a7) est beaucoup plus petit que 0,0001. Donc, à deux décimales près, la valeur de (a7 + 1) / (2a7) est 0,50.
En conclusion, le chiffre des unités pour a7 est 3, a7 est plus grand ou égal à 10^100, et (a7 + 1) / (2a7) est environ égal à 0,50.
Prépa Examens
Concours et examens UK
Terminale

1, et 2, et… 4 valeurs absolues !
Dans cette vidéo, nous avons un exercice de mathématiques qui consiste à trouver toutes les solutions d'une équation. L'exercice se décompose en plusieurs étapes. Tout d'abord, nous devons comprendre qu'il s'agit d'un exercice où la précision et l'efficacité sont requises, plutôt que la créativité. Ensuite, nous différencions les différentes valeurs absolues selon les intervalles donnés. Nous combinons ensuite ces valeurs absolues pour obtenir une expression pour f(x). Ensuite, nous essayons de résoudre l'équation f(2x) = x + 2 sur chaque intervalle en vérifiant que les solutions obtenues sont valides pour chaque intervalle. L'équation a une solution valide sur l'intervalle -∞ à -1 et sur l'intervalle 1 à +∞. En revanche, il n'y a pas de solution valide sur les intervalles -1 à 0 et 0 à 1. Ainsi, la solution de l'équation est l'ensemble des réels entre 2 et +∞, inclus, ainsi que la solution unique -2. La vidéo conclut en encourageant les spectateurs à poser des questions et à partager d'autres solutions élégantes.
Prépa Examens
Concours et examens UK
Terminale

4 questions en une
Dans cet exercice de Cambridge, nous devons répondre à quatre questions en une. La première question concerne les puissances de logarithmes. L'auteur nous rappelle de toujours appliquer le logarithme lorsque nous avons une puissance complexe. Dans ce cas, nous devons vérifier si a puissance log de b est égale à b puissance log de a pour tout a et b positifs. Après avoir vérifié que a est positif, nous appliquons le logarithme des deux côtés et obtenons log a puissance log b égal à log b puissance log a. En simplifiant, nous trouvons log b multiplié par log a égal à log a multiplié par log b, ce qui est vrai. Donc, la première affirmation est vraie.
La deuxième question concerne les fonctions trigonométriques. On nous demande de vérifier si cos sin θ est égal à sin cos θ pour tout θ réel. Intuitivement, nous pouvons sentir que cette affirmation est fausse et nous pouvons la vérifier en utilisant un contre-exemple. En prenant θ égal à π sur 2, nous pouvons voir que cos sin π sur 2 est égal à cos 1, qui est différent de 0, tandis que sin cos π sur 2 est égal à sin 0, qui est égal à 0. Donc, cette affirmation est fausse.
La troisième question concerne un polynôme P. On nous demande s'il existe un polynôme P tel que P(θ) - cos(θ) soit inférieur ou égal à 10 puissance -6 pour tout θ. Nous pouvons intuitivement sentir
Prépa Examens
Concours et examens UK
Terminale

Dériver 1, 2, ... 3 fois !!
Dans cet exercice, nous étudions une fonction complexe, F2x, ainsi que d'autres fonctions F, G et H qui augmentent en difficulté. Nous devons démontrer différentes propriétés de ces fonctions, telles que leur positivité sur certains intervalles.
Tout d'abord, nous examinons la fonction F et remarquons qu'elle est strictement croissante sur l'intervalle [0, +∞), car sa dérivée est positive ou nulle. En utilisant cette propriété, nous montrons que F2x est positif ou nul pour tout x positif, ce qui répond à la première question.
Ensuite, nous passons à la fonction G et effectuons des calculs similaires pour montrer qu'elle est également positive sur l'intervalle [0, π/2). En dérivant deux fois, nous prouvons que la dérivée seconde de G est positive sur cet intervalle, ce qui implique que la dérivée première de G est croissante et que G est positive.
Nous répétons cette procédure pour la fonction H et démontrons qu'elle est positive sur l'intervalle [0, π/4). En dérivant plusieurs fois, nous constatons que la dérivée troisième de H est positive, ce qui entraîne une croissance stricte de la dérivée seconde de H et donc une positivité de H.
Enfin,
Prépa Examens
Concours et examens UK
Terminale

Une suite avec un produit infini !
Aucun résumé n'est disponible pour cette vidéo
Prépa Examens
Concours et examens UK
Terminale
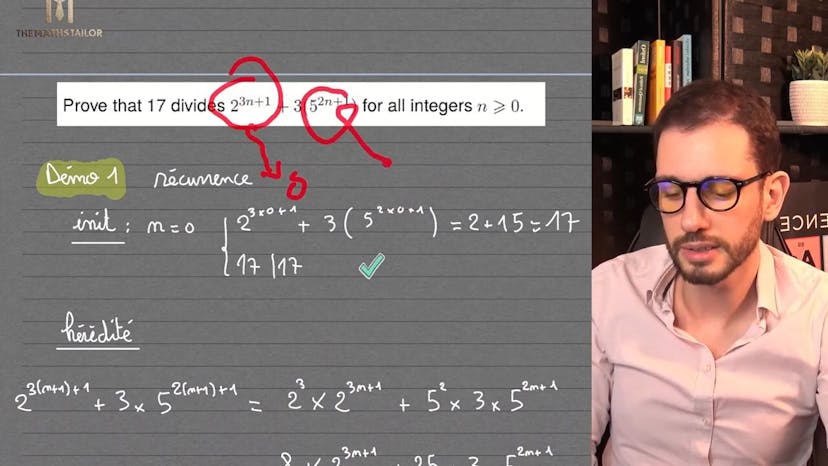
3 démos d'arithmétique de terminale !
Dans cette vidéo, le professeur présente trois démonstrations pour résoudre un exercice d'arithmétique. Il explique que la première méthode consiste à utiliser la récurrence, en montrant que l'expression est divisible par 17 pour n=0 et en faisant apparaître le terme n+1 dans l'expression. La deuxième démonstration utilise les tables de congruence, mais elle se révèle trop longue et complexe pour cet exercice. Finalement, le professeur propose une troisième méthode plus efficace, qui consiste à séparer les termes en puissance n dans l'expression et à remarquer que 8 et 25 sont séparés d'une distance de 17. Ainsi, en utilisant les congruences, il démontre que l'expression est congrue à 0 modulo 17. Il conclut en encourageant les élèves à poser des questions et en annonçant une prochaine vidéo.


