Cours de Suites numériques en Ligne par les Meilleurs Professeurs - Suites numériques

Introduction à la récurrence

Dans cette vidéo, le cours introduit le principe de la méthode de démonstration par récurrence, en se basant sur l'exemple de la formule de la somme des n entiers consécutifs. La méthode de démonstration par récurrence s'applique uniquement aux propriétés dépendant de n. Il est important de noter que la méthode de récurrence ne fournit pas une formule, mais plutôt une manière de démontrer une formule dont on a déjà une intuition. Pour démontrer la propriété, on commence par une initialisation, où la propriété est vérifiée pour une valeur spécifique de n. Ensuite, on prouve que si la propriété est vraie pour un certain n, alors elle est également vraie pour n+1, ce qui permet de conclure que la propriété est vraie pour tous les entiers. Il est crucial de ne pas oublier cette initialisation, car sans elle, la méthode de récurrence ne fonctionnera pas. Le cours souligne également trois points clés à retenir : le principe général de la récurrence (initialisation et hérédité), l'importance de l'initialisation (qui peut commencer à n=0, n=1, etc.) et l'inégalité de Bernoulli, qui peut être démontrée par récurrence. En termes de méthode, la récurrence peut être appliquée aux suites, utilisée pour démontrer une formule générale basée sur quelques termes, ou pour résoudre des problèmes plus complexes nécessitant différentes approches de la transmission.

Concept et rédaction

Dans cette vidéo, le professeur explique le principe de la récurrence en mathématiques. Il rappelle que pour démontrer une propriété par récurrence, il faut montrer qu'elle est vraie pour un entier donné, puis que si elle est vraie pour cet entier, elle est également vraie pour l'entier suivant. En utilisant cette "pichenette initiale" et cette transmission, on peut prouver que la propriété est vraie pour tous les entiers. Le professeur insiste sur l'importance de la rédaction dans la démonstration par récurrence. Il souligne qu'il faut toujours conclure la démonstration en affirmant que la propriété est vraie pour tout entier. Si cette conclusion n'est pas incluse, il est possible de perdre des points. Il recommande ainsi de donner une vision d'ensemble de la démonstration après avoir montré l'initialisation et la transmission de la propriété. Le professeur mentionne également que dans environ 10% des exercices, la démonstration par récurrence commence avec un entier différent de zéro, ce qui peut dérouter les étudiants. Il donne l'exemple d'une suite récurrente où il faut prouver la propriété pour tout entier supérieur à 2, au lieu de 0. Enfin, le professeur rappelle aux étudiants de se référer aux consignes spécifiques de leur professeur concernant la rédaction de la démonstration par récurrence, afin d'obtenir de bons résultats. Il invite également les étudiants à poser leurs questions dans la FAQ du cours pour obtenir des éclaircissements supplémentaires.

Pourquoi l'initialisation ?

Dans cette vidéo, on aborde l'importance de l'initialisation dans le contexte de la transmission de propriétés. L'orateur mentionne un exemple spécifique, celui de la propriété P2N, qui affirme que 2 puissance N est divisible par 3, bien que cela soit incorrect. Cependant, cette propriété est transmise, c'est-à-dire que si elle est vraie pour un instant N, elle le sera également pour l'instant N+1. Cela souligne l'importance de l'initialisation, même si celle-ci peut sembler fastidieuse. L'orateur conclut en expliquant qu'il est crucial de faire les initialisations nécessaires pour chaque propriété, car il est peu probable de trouver une initialisation pour des propriétés comme P2N. Cette vidéo est un bonus pour les étudiants, leur montrant que les professeurs insistent sur l'initialisation non pas pour les embêter, mais parce qu'il y a des implications importantes derrière cela. N'hésitez pas à poser des questions ou à consulter la FAQ ci-dessous.

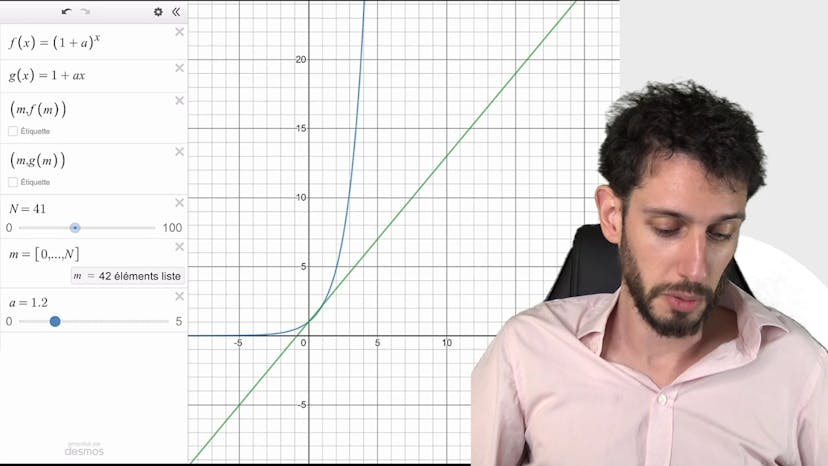
Inégalité de Bernoulli : visuel

Dans cette vidéo, le professeur explique l'inégalité de Bernoulli, qui stipule que pour toute valeur réelle A strictement positive et pour tout entier naturel N, on a l'inégalité 1 + A^N ≥ 1 + NA. Il mentionne que cette inégalité est étudiée dans le cadre de la récurrence car elle peut être démontrée de manière simple en utilisant le principe de récurrence. Pour donner une intuition graphique de cette formule, le professeur compare les deux éléments de l'inégalité à des fonctions. Il remarque que la partie de gauche, A^N, a une forme exponentielle, tandis que la partie de droite, NA, a une forme affine. Il explique que cela traduit le fait qu'une fonction exponentielle monte beaucoup plus vite qu'une fonction affine et donc est plus grande. Pour illustrer cette idée, le professeur utilise une simulation graphique où il fait varier différents paramètres, notamment la valeur de A. Il montre que pour certaines valeurs de A, la fonction exponentielle est toujours au-dessus de la fonction affine, tandis que pour d'autres valeurs, la fonction affine dépasse la fonction exponentielle dans un certain intervalle. Cependant, il souligne que cela n'est pas important pour l'inégalité de Bernoulli, car ce qui compte, c'est la suite des points représentés par les coordonnées entières des fonctions. En observant les points de la suite définie par les fonctions, le professeur constate que, dès le point 2, la suite représentée par la fonction exponentielle est toujours au-dessus de celle représentée par la fonction affine. Il mentionne également que pour les entiers 0 et 1, les deux fonctions sont égales, ce qui peut être vérifié en remplaçant ces valeurs dans l'inégalité de Bernoulli. Le professeur conclut en soulignant l'utilité de cette inégalité pour les démonstrations mathématiques et invite les spectateurs à poser des questions et utiliser la simulation graphique partagée pour mieux comprendre l'inégalité de Bernoulli.

Récurrence et croissance

La démonstration par récurrence est une technique de preuve mathématique utilisée pour prouver qu'une propriété est vraie pour une séquence infinie de nombres. Dans cet exemple, nous devons montrer par récurrence que la suite Un est strictement décroissante. Pour commencer, nous définissons la propriété P2n, qui est vraie pour le rang n. Dans ce cas, nous devons montrer que Un+1 est plus petit que Un. Nous voulons prouver que P2n est vrai pour tous les rangs naturels n. Nous commençons par l'initialisation en calculant U1 et U0 pour n=0. Dans cet exemple, U1 est égal à -2 et U0 est égal à 2, ce qui est correct. Ensuite, nous passons à l'hérédité. Nous supposons que l'hypothèse de récurrence, c'est-à-dire que Un+1 est plus petit que Un, est vraie pour le rang n. Nous voulons montrer que Pn+1 est vrai. Nous utilisons la relation de récurrence Un+1 = 2Un - 6 pour montrer que Un+2 est plus petit que Un+1. Pour simplifier cette démonstration, nous définissons la fonction f(x) = 2x - 6, qui est une fonction affine strictement croissante. Puisque Un+1 est plus petit que Un, nous composons cette relation par la fonction f. Ainsi, nous obtenons Un+2 qui est également plus petit que Un+1. En conclu

Conjecture puis récurrence

Dans ce cours, nous allons voir comment utiliser la démonstration par récurrence pour calculer la somme des entiers de 1 à n. La formule de la somme des entiers naturels est n(n + 1)/2. Pour utiliser la démonstration par récurrence, il faut connaître le résultat que l'on veut démontrer. Dans cet exemple, nous avons besoin de connaître la formule de la somme des entiers naturels. Nous commençons par poser la proposition p2n, qui est que la somme de 1 à n vaut n(n + 1)/2. Nous montrons ensuite que p2n est vrai pour tout n. Nous commençons par l'initialisation en vérifiant que la formule est vraie pour n = 1. Ensuite, nous passons à l'hérédité en supposant que p2n est vrai pour un n quelconque et nous voulons montrer que p2n+1 est vrai. Pour cela, nous remplaçons chaque occurrence de n par n + 1 dans l'expression au rang n. Nous appliquons la formule de la somme des entiers naturels à p2n et nous obtenons n(n + 1)/2 + n + 1. En simplifiant cette expression, nous obtenons n(n + 1)/2 + 2(n + 1)/2, ce qui donne (n + 1)(n + 2)/2. Ainsi, nous avons démontré que p2n+1 est vrai. En conclusion, d'après le principe de récurrence, nous avons prouvé que la somme des entiers de 1 à n est égale à n(n + 1)/2 pour tout entier naturel non nul n. C'est ainsi que nous pouvons utiliser la démonstration par récurrence pour calculer cette somme.

Hérédité : comment démarrer ?

La démonstration par récurrence est une méthode utilisée en mathématiques pour prouver une propriété pour tous les entiers naturels (n). Dans cette vidéo, l'accent est mis sur la démonstration de l'hérédité, qui est la partie la plus complexe de la méthode. Il existe deux cas possibles pour démontrer l'hérédité. Dans les deux cas, l'hypothèse de récurrence et ce que l'on veut montrer doivent être reliés. Le premier cas consiste à partir de l'hypothèse de récurrence (Pn) et à aboutir à Pn + 1. Le deuxième cas consiste à partir de Pn + 1 et à utiliser P2n pour conclure. Les deux méthodes sont possibles et peuvent être utilisées en fonction de l'exercice. Pour illustrer ces deux cas, un exemple simple est utilisé. Une suite (U) est définie par récurrence avec U0 = 5 et Un+1 = 3Un + 6. L'objectif est de montrer que U1 est strictement positif pour tout n. La démonstration commence par poser P2n, qui est U strictement supérieur à 0. L'initialisation ne pose aucun problème car U0 vaut 5. Ensuite, l'hérédité est démontrée en utilisant les deux cas possibles. Dans le premier cas, on part de l'hypothèse de récurrence (Pn) en supposant que U est supérieur à 0. En multipliant par 3 et en ajoutant 6, on obtient que 3Un + 6 est supérieur à 6, qui est lui-même supérieur à 0. Ainsi, Un+1 est supérieur à 0. Dans le deuxième cas, on part de Pn+1, c'est-à-dire de Un+1, et on utilise l'hypothèse de récurrence (Pn). Comme Un est supérieur à 0, on peut conclure que Un+1 est également supérieur à 0. Les deux méthodes sont possibles et peuvent être utilisées selon les besoins. Il n'y a pas de meilleure méthode, tout dépend de l'exercice. Si vous rencontrez des difficultés avec l'une des méthodes, vous pouvez essayer l'autre. En conclusion, la démonstration par récurrence est une méthode utilisée pour prouver une propriété pour tous les entiers naturels. L'hérédité, qui est la partie la plus complexe, peut être démontrée en utilisant deux cas possibles. Les deux méthodes sont viables et peuvent être utilisées en fonction des besoins de l'exercice.

Test video

Aucun résumé n'est disponible pour cette vidéo

Hérédité mais...

L'exercice consiste à démontrer que la proposition "9 divise 10 puissance n plus 1" est vraie pour tout entier naturel n. La question 1 demande de démontrer que si la proposition est vraie pour un entier n, alors elle est aussi vraie pour n plus 1. Pour cela, il faut utiliser le principe de récurrence. Le professeur souligne qu'il ne faut pas surinterpréter les énoncés et se focaliser uniquement sur la démonstration de l'imp

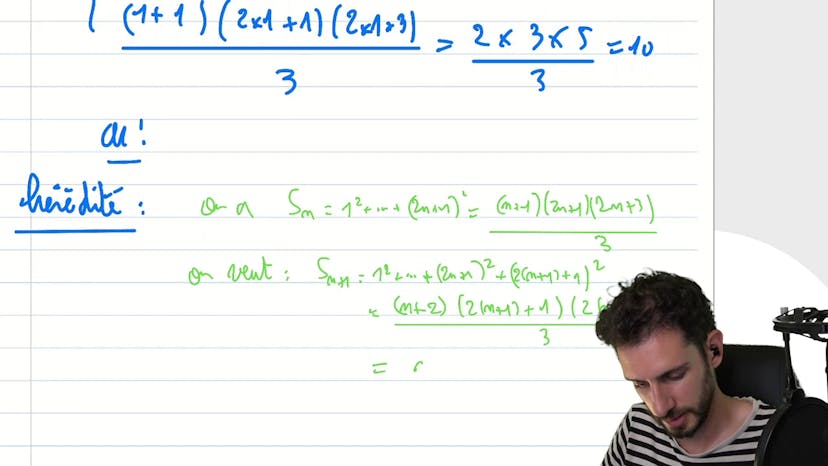
Avec une Somme

Ce cours traite d'une démonstration mathématique. L'objectif est de montrer que pour tout entier n, la somme des carrés des nombres impairs jusqu'à n est égale à la formule 2n + 3. Le cours commence par expliquer l'importance d'écrire clairement ce que l'on veut démontrer. Ensuite, l'auteur utilise des notations mathématiques pour étayer sa démonstration par récurrence. Il commence par l'initialisation, en montrant que l'égalité est vérifiée pour n = 1. Ensuite, il passe à l'hérédité, en supposant que l'égalité est vraie pour n, puis en démontrant qu'elle est également vraie pour n+1. Pour cela, il factorise certaines expressions et effectue des calculs, en utilisant la formule de la somme des impairs. En fin de compte, il conclut en montrant que l'égalité est vérifiée pour tout entier n.

Majoration 'simple'

Dans ce cours, nous cherchons à démontrer une propriété mathématique par récurrence. Nous commençons par initialiser la démonstration en montrant que pour n=1, la propriété est vérifiée. Ensuite, nous supposons que la propriété est vraie pour un certain n. Nous utilisons cette supposition pour montrer que la propriété est également vraie pour n+1. Pour cela, nous manipulons des équations et des inégalités afin de prouver que la propriété est conservée à chaque étape. Enfin, nous concluons que la propriété est démontrée pour tous les n.