 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Corrigés de BAC
Bac Maths
MPSI/PCSI

Fonctions - Métropole 2022
Dans cet exercice, nous étudions différentes questions sur les fonctions logarithmes.
La première question concerne l'équation f(2x) = log(1 + x^2) = 2022. En passant à l'exponentielle des deux côtés de l'équation, nous obtenons 1 + x^2 = e^2022. Comme e^2022 est strictement positif, l'équation admet deux solutions : la racine carrée de e^2022 et son opposé.
La deuxième question porte sur la convexité de la fonction G définie par G(x) = x log(x) - x^2. En calculant la dérivée seconde de G, nous pouvons observer que celle-ci est positive entre 0 et 1/2, puis devient négative à partir de 1/2. Par conséquent, la fonction G a un unique point d'inflexion.
La troisième question demande de trouver une primitive de la fonction f définie par f(x) = x / (1 - x^2). En identifiant u' / u, nous pouvons reconnaître la dérivée de log(1 - x^2). Ainsi, la primitive de f est -1.5 log(1 - x^2).
La quatrième question concerne l'ensemble de définition de la fonction associée à l'expression log(-x^2 - x + 6). Comme nous savons que le logarithme est défini lorsque son argument est strictement positif, nous devons étudier le signe du polynôme -x^2 - x + 6. En déterminant son discriminant, nous trouvons deux racines, et en analysant les signes entre et à l'extérieur de ces racines, nous concluons que l'ensemble de définition est (-3, 2).
Enfin, la dernière question concerne une inéquation logarithmique. En simplifiant l'expression, nous obtenons x + 3 < (x + 1)^2. Après étude d'un polynôme du second degré, nous déterminons que l'inégalité est vérifiée pour x appartenant à (-∞, -2) U (1, +∞).
Corrigés de BAC
Bac Maths
MPSI/PCSI

Probabilités - Métropole 2022
Dans cet exercice de bac sur les probabilités, nous devons calculer des probabilités en utilisant des intersections et des arbres de probabilités. Nous devons également utiliser des probabilités conditionnelles et parler d'indépendance. Dans la deuxième partie de l'exercice, nous devons travailler avec des variables aléatoires qui suivent une loi normale.
Dans la première partie, nous avons un coyote qui peut être malade (M) ou non malade (non M). Un test est réalisé et peut être positif (T) ou négatif (non T). On nous donne les informations suivantes : si le coyote est malade, le test est positif dans 97% des cas, et s'il n'est pas malade, le test est négatif dans 95% des cas.
Nous devons d'abord calculer la probabilité que le coyote soit malade et que son test soit positif. Cette probabilité est donnée par l'intersection entre M et T, soit 0,7 * 0,97 = 0,679.
Ensuite, nous devons démontrer que la probabilité de T est égale à 0,694. Nous utilisons la formule des probabilités totales en utilisant les probabilités conditionnelles. Après calcul, nous trouvons bien 0,694.
Nous devons également calculer la valeur prédictive positive du test, c'est-à-dire la probabilité que le coyote soit malade sachant que son test est positif. En utilisant la formule des probabilités conditionnelles, nous trouvons une valeur de 0,978.
Par analogie avec la question précédente, nous devons défin
Corrigés de BAC
Bac Maths
MPSI/PCSI

Géométrie - Métropole 2022
Dans cet exercice de géométrie dans l'espace, nous sommes confrontés à différents problèmes liés à la géométrie et à la trigonométrie. Les principales étapes de l'exercice sont les suivantes :
1. Trouver les coordonnées des points E, F, G et K dans le repère donné.
2. Montrer que le vecteur N est orthogonal au plan E, G, K en effectuant des calculs de produit scalaire.
3. Trouver l'équation cartésienne du plan E, G, K en utilisant le vecteur normal et un point du plan.
4. Déterminer une représentation paramétrique de la droite D orthogonale au plan E, G, K et passant par F.
5. Calculer les coordonnées du projeté orthogonal de F sur le plan E, G, K en résolvant un système d'équations.
6. Justifier que la longueur LF est égale à 2/3 en utilisant la formule de calcul de distance dans l'espace.
7. Calculer l'aire du triangle EFG et en déduire le volume du tétraèdre EFGK en utilisant les formules appropriées.
8. Déterminer le volume du tétraèdre FPMN en utilisant le théorème de la droite des milieux.
En résumé, cet exercice aborde différents concepts de géométrie et de trigonométrie dans l'espace, tels que l'orthogonalité, les équations cartésiennes, les représentations paramétriques, les projetés orthogonaux, les longueurs, les aires et les volumes dans le contexte d'un tétraèdre.
Corrigés de BAC
Bac Maths
MPSI/PCSI

Suites et fonctions - Polynésie 2022
Aucun résumé n'est disponible pour cette vidéo
Corrigés de BAC
Bac Maths
MPSI/PCSI
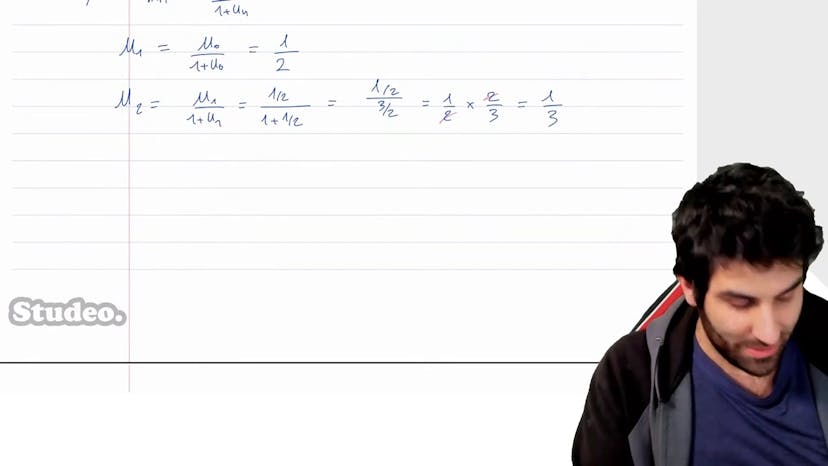
Suites - Polynésie 2022
Aucun résumé n'est disponible pour cette vidéo
Corrigés de BAC
Bac Maths
MPSI/PCSI

Probabilités - Polynésie 2022
Dans cet exercice, nous étudions les probabilités liées à une maladie et à un test de dépistage. Le contexte se base sur l'hypothèse de 7% de la population touchée par cette maladie. Le test de dépistage donne des faux négatifs dans 20% des cas pour les personnes malades, et des faux positifs dans 1% des cas pour les personnes non malades. Les questions posées portent notamment sur la probabilité d'être malade et d'avoir un test positif, la fiabilité du test, ainsi que le nombre minimum de personnes à tester pour qu'au moins l'une d'entre elles ait un test positif avec une probabilité supérieure à 99%. Les probabilités sont calculées en utilisant des arbres pondérés, des formules de probabilités conditionnelles et la loi binomiale. En conclusion, il est recommandé de privilégier la connaissance de la probabilité d'être malade sachant que le test est positif, dans un contexte de dépistage de maladie. Enfin, il est nécessaire de tester au moins 69 personnes pour avoir une probabilité supérieure à 99% qu'au moins l'une d'entre elles ait un test positif.
Corrigés de BAC
Bac Maths
MPSI/PCSI

Géométrie - Polynésie 2022
Aucun résumé n'est disponible pour cette vidéo
Corrigés de BAC
Bac Maths
MPSI/PCSI

Fonctions - Asie 2022
Aucun résumé n'est disponible pour cette vidéo
Corrigés de BAC
Bac Maths
MPSI/PCSI

Probabilités - Asie 2022
Cet exercice porte sur les probabilités, les probabilités conditionnelles, les indépendances et les variables aléatoires. La première partie concerne les événements et les prob
Corrigés de BAC
Bac Maths
MPSI/PCSI

Suites - Asie 2022
Dans cet exercice de BAC sur les suites avec de l'algorithmique et de la programmation, on étudie le développement d'une bactérie en utilisant des probabilités. On modélise le développement de la bactérie avec certaines hypothèses : elle a une probabilité de 0,3 de mourir sans descendance et une probabilité de 0,7 de se diviser en deux bactéries. On utilise la relation de récurrence P_n+1 = 0,3 + 0,7 * P_n^2 pour calculer les valeurs de P_1 et P_2. On obtient P_1 = 0,363 et P_2 = 0,3922383. Ces valeurs indiquent que la bactérie a plus de chances d'avoir au moins 1 ou 2 descendants que 0.
Ensuite, on nous demande de déterminer la probabilité, arrondie à 10^-3, d'obtenir au moins 11 générations de bactéries à partir d'une bactérie de ce type. On utilise la relation P_n <= 0,5 pour montrer que P_10 est l'inégalité exacte. Donc, la probabilité d'obtenir au moins 11 générations est égale à 1 - P_10, soit environ 0,571.
On formule ensuite des conjectures sur les variations et la convergence de la suite P_n. En observant le tableau, on voit que les termes de la suite semblent converger vers 0,428, en étant croissants. On conclut que la suite est croissante et convergente.
Par récurrence sur n, on démontre que pour tout entier naturel n, P_n < P_n+1 et les deux sont compris entre 0 et 0,5.
On justifie ensuite que la suite est convergente en montrant que P_n < P_n+1, ce qui prouve que la suite est croissante, et que tous les termes de la suite sont inférieurs à 0,5.
On détermine alors la limite de la suite en résolvant l'équation 0,3 + 0,7 * l^2 = l, où l est la limite de la suite. On trouve l = 3/7, soit environ 0,430.
Enfin, on écrit une fonction en Python qui renvoie les n premiers termes de la suite. On initialise le tableau avec la valeur de P_0, puis on utilise une boucle pour calculer les termes suivants en utilisant la relation de récurrence. On ajoute chaque terme calculé au tableau avec la fonction append, et on renvoie le tableau complet.
Cet exercice permet de mettre en pratique les concepts de suites, probabilités et programmation, en étudiant le développement d'une bactérie avec des hypothèses et des calculs de probabilités. On calcule les valeurs de la suite, interprétons les résultats dans le contexte, démontrons des propriétés sur la
Corrigés de BAC
Bac Maths
MPSI/PCSI

Fonctions - Nouvelle Calédonie 2022
Cet exercice porte sur l'étude des fonctions, des fonctions logarithmes et de la convexité. Il comporte plusieurs questions classiques telles que le calcul de limite, la dérivation, le tableau de variations et le théorème des valeurs intermédiaires. La question qui se démarque concerne la position relative d'un segment par rapport à la courbe d'une fonction.
Dans la première partie, on calcule la limite de la fonction f(x) en 0. On sépare la fonction en polynôme et logarithme et on obtient que f(x) tend vers moins l'infini. Cela indique la présence d'une asymptote verticale à la courbe de f(x) pour x = 0.
Ensuite, on détermine la limite de f(x) quand x tend vers plus l'infini. On factorise la fonction et on constate que f(x) tend vers plus l'infini.
On détermine ensuite la dérivée de f(x) et on étudie le signe de cette dérivée. On trouve que f(x) est croissante sur l'intervalle 0 à √2 et décroissante sur l'intervalle √2 à plus l'infini.
On montre ensuite que l'équation f(x) = 0 admet une unique solution dans l'intervalle [4, 5] en utilisant le théorème des valeurs intermédiaires.
On admet la dérivée seconde et on étudie la convexité de la fonction f(x). On trouve que f(x) est concave sur l'intervalle [0, √2] et convexe sur l'intervalle [√2, +∞].
Enfin, on utilise les informations précédentes pour déterminer la position relative du segment AM (corde) par rapport à la courbe de f(x). Si le point M est compris entre 0 et √2, le segment AM est en dessous de la courbe. Si le point M est compris entre √2 et plus l'infini, le segment AM est au-dessus de la courbe.
Cet exercice permet de mettre en pratique plusieurs concepts importants en étude de fonctions et en calcul de limites, tout en abordant un problème un peu plus original concernant la position relative d'un segment par rapport à une courbe.
Corrigés de BAC
Bac Maths
MPSI/PCSI

Suites et fonctions - Nouvelle Calédonie 2022
Dans cet exercice, nous étudions la fonction exponentielle et une suite définie par récurrence. Tout d'abord, nous calculons les premiers termes de la suite, u1 et u2, en utilisant la fonction f définie par f(x) = x^3 * e^x. Ensuite, nous démontrons par dérivation que pour tout x réel, f'(x) = x^2 * e^x * (x+3). En utilisant les variations de cette fonction, nous justifions le tableau de variation de f. Enfin, nous démontrons par récurrence que pour tout entier naturel n, -1 ≤ un ≤ 0. Pour cela, nous montrons que la proposition est vraie au rang 0, et nous supposons qu'elle soit vraie au rang n pour montrer qu'elle est vraie au rang n+1. En utilisant cette propriété, nous déduisons que la suite un est croissante et majorée par 0, et donc elle converge vers un réel l ≤ 0. En résolvant l'équation f(x) = x, nous trouvons que l est nécessairement égal à 0. Ainsi, nous avons déterminé la limite de la suite un.


