 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths Spé
Analyse
Terminale
Comparaison et encadrement
Ce cours traite de deux théorèmes qui permettent de comparer et d'étudier des fonctions de manière efficace, sans les étudier en détail. Le premier théorème est celui de la comparaison, qui dit que si une fonction f tend vers l'infini et qu'une autre fonction g est plus grande que f, alors f va pousser g vers l'infini. Le théorème d'encadrement, également appelé "théorème des gendarmes", est le second théorème présenté. Il stipule que si deux fonctions f et h encadrent une fonction g et tendent toutes deux vers la même limite, alors g tend également vers cette même limite. Le cours utilise des exemples pour illustrer ces théorèmes, notamment avec des graphiques pour mieux visualiser les concepts. Ces théorèmes sont particulièrement utiles pour résoudre des exercices de mathématiques impliquant des limites de fonctions.
Maths Spé
Analyse
Terminale
Croissance comparée exp et ln
La croissance comparée est la théorie selon laquelle l'exponentielle l'emporte sur n'importe quelle puissance de x. En d'autres termes, si vous divisez E2x par x puissance n, la limite est toujours l'infini. L'exponentielle domine complètement sur les x puissances n. La propriété des puissances est utilisée pour appliquer cette théorie à l'exponentielle. On utilise également un changement de variable pour démontrer que la quantité tend vers 0 lorsque x tend vers moins l'infini. Cette méthode peut également être utilisée pour trouver des solutions simples à certains calculs de limites.
Maths Spé
Analyse
Terminale

Limite des fonctions composées
Ce cours parle des limites de fonction, plus précisément de la composition de fonctions. L'exemple donné est celui de la limite de la racine de 1+ex lorsque x tend vers l'infini. Pour trouver cette limite, on décompose la fonction en deux parties: 1+ex et la racine de cette fonction. On utilise ensuite un théorème mathématique qui nous autorise à faire cette composition. La limité de la racine est prouvée en utilisant le comportement de la fonction racine envers la limite de 1+ex. Le théorème stipule que si la limite de f(x) tend vers b et que la limite de g(x) tend vers 1 quand f(x) tend vers b, alors la limite de g(f(x)) tend vers 1. En résumé, ce cours explique comment utiliser la composition de fonctions pour trouver des limites, en utilisant un théorème mathématique.
Maths Spé
Analyse
Terminale
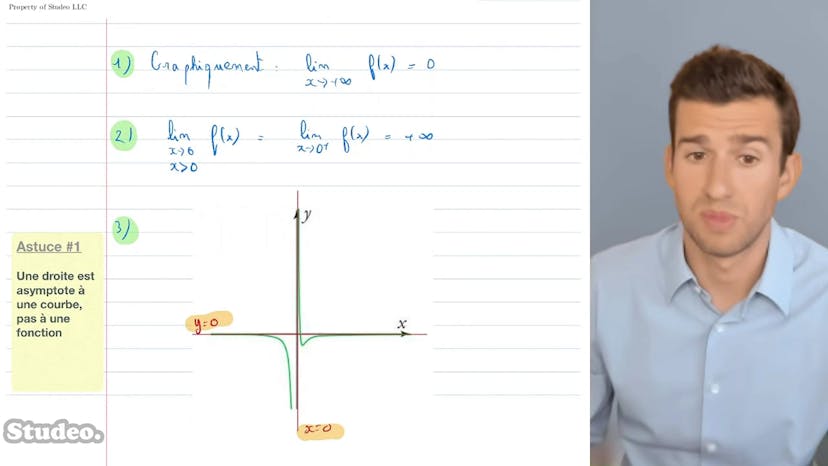
Analyse graphique
Dans ce cours, nous examinons les limites de fonctions en utilisant une analyse graphique. Nous examinons une fonction tracée et déterminons ses limites en examinant son comportement lorsque x tend vers plus ou moins l'infini. En utilisant cette méthode, nous pouvons identifier les asymptotes verticales et horizontales de la courbe. Les équations des asymptotes sont de la forme y = a pour une droite horizontale et x = a pour une droite verticale. Nous faisons également deux remarques: premièrement, une droite est l'asymptote à une courbe, pas à une fonction. Deuxièmement, une droite peut être l'asymptote en deux endroits.
Maths Spé
Analyse
Terminale

Calcul limite en un point fini par factorisation
Dans ce cours, nous apprenons comment trouver une limite en 1 pour une fonction avec une forme indéterminée. Pour cela, nous pouvons factoriser la fonction pour lever l'indétermination. Le premier exemple est facile à factoriser à l'aide de l'identité remarquable, ce qui nous donne une limite de 0. Le deuxième exemple nécessite la factorisation d'un polynôme à l'aide de la méthode classique pour trouver les racines. Nous trouvons ainsi 2 racines, que nous pouvons utiliser pour factoriser la fonction et trouver une limite de 1/2. Nous notons que la fonction tend vers 0 à gauche et à droite de 1, et précisons ses limites en 1+, 1- et leur influence sur le quotient avec une autre fonction. Cette méthode est utile lorsque nous pouvons factoriser la fonction pour simplifier le calcul des limites.
Maths Spé
Analyse
Terminale

Determiner une asymptote + étude
Pour trouver les asymptotes d'une fonction, il faut regarder en plus l'infini, en moins l'infini et les bords de l'ensemble de définition de la fonction. Par exemple, pour la fonction f(x) = -2/(1-x) définie sur R privé de 1, il faut regarder en moins et plus l'infini, ainsi qu'en 1. En moins et plus l'infini, on a une asymptote horizontale d'équation y = 0. En 1, il y a une asymptote verticale d'équation x=1. Pour déterminer si on tend vers plus ou moins à un point donné, il faut prendre des valeurs autour pour être sûr.
Maths Spé
Analyse
Terminale
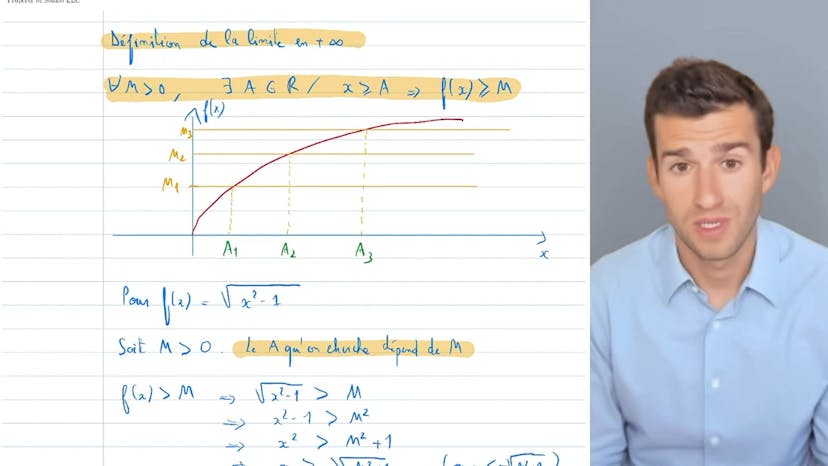
Calcul de limite infinie avec la définition (trouver un A)
Dans ce cours, nous avons abordé la définition formelle de la limite, qui peut sembler difficile à comprendre pour certains élèves. Nous avons expliqué que la limite est atteinte lorsque la fonction tend vers une valeur infinie, ce qui signifie qu'à un certain moment, la fonction dépassera toujours un certain point. Nous avons utilisé l'exemple d'une fonction racine carrée pour illustrer cette idée. Ensuite, nous avons examiné une autre fonction, racine de x au carré moins un, et avons expliqué comment trouver la valeur de a qui convient à un certain point m. Cela implique de résoudre une inéquation. Nous avons montré comment cette approche peut être utilisée pour démontrer que la fonction tend vers l'infini lorsque x tend vers l'infini.En somme, la résolution d'équations est la méthode clé utilisée pour résoudre les problèmes concrets et pour pratiquer la définition formelle de la limite.
Maths Spé
Analyse
Terminale
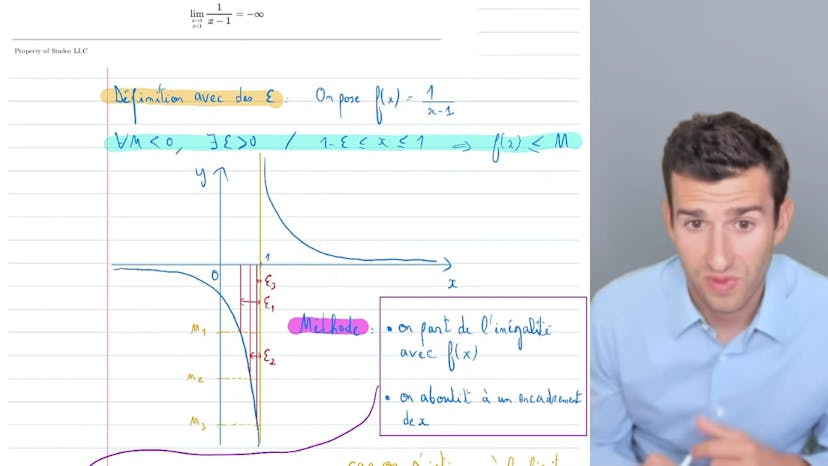
Calcul de limite finie avec la définition (trouver un epsilon)
Dans ce cours, on apprend à calculer la limite infinie en utilisant la définition avec les epsilon. Le but est de montrer que la fonction tend vers moins l'infini en un réel fixé. Pour cela, on prend un réel négatif m et on cherche à résoudre f2x inférieur à m. On trouve alors un encadrement de x qui permet de déterminer un intervalle où la fonction est inférieure à m. On utilise l'inverse de la fonction pour vérifier que l'on est sur le bon intervalle. Le but est de trouver le y qui convient en déroulant les calculs petit à petit. L'exercice demande de la pratique, mais avec de l'exercice, on peut y arriver.
Maths Spé
Analyse
Terminale

Forme indéterminée : utilisation du terme plus haut degré
La méthode pour déterminer les limites infinies des polynômes et des fonctions rationnelles est de factoriser par le terme de plus haut degré, également appelé le terme de Claudegris. Cette technique permet de résoudre les indéterminations et déterminer la limite facilement. Pour les polynômes, on factorise par x^4 et on obtient 1+4/x-2/x^3, qui tend vers 0 en plus/moins infini, et donc la limite est plus infinie. Pour les fonctions rationnelles, on factorise le numérateur et le dénominateur par le terme de Claudegris, et on fait attention au signe. En cas d'erreur, il suffit de vérifier la factorisation. Cette méthode est simple et efficace et il est important de la maîtriser en s'entraînant.
Maths Spé
Analyse
Terminale

Forme indéterminée : Méthode quantité conjuguée
La méthode de la quantité conjuguée est utilisée dans les cas où il y a des racines car celles-ci ne s'additionnent pas bien. Pour supprimer ces racines, on multiplie souvent par la quantité conjuguée. Par exemple, si une fonction a une forme indéterminée lorsque x tend vers 0, on peut utiliser la quantité conjuguée pour lever cette indétermination. Si la fonction présente une forme indéterminée en l'infini, on utilise également la quantité conjuguée pour faire apparaître un plus dans l'expression. En utilisant cette méthode, on peut supprimer les racines et lever l'indétermination, ce qui permet de déterminer la limite de la fonction.
Maths Spé
Analyse
Terminale

Limites : la Croissance comparée
La croissance comparée est une méthode utile pour étudier les fonctions. Elle consiste à comparer les croissances de différentes fonctions pour déterminer leur comportement en cas d'extrêmes. Dans ce cours, on étudie deux fonctions, E de X sur X et H, en utilisant la croissance comparée. La première fonction tend toujours vers plus infini, même si N est très grand. La seconde fonction est plus complexe mais on peut utiliser un changement de variable pour la ramener à la croissance comparée de référence. En général, l'exponentielle l'emporte sur toutes les puissances de X, tandis que le logarithme perd. Il est important de retenir ces références pour pouvoir lever la détermination facilement.
Maths Spé
Analyse
Terminale
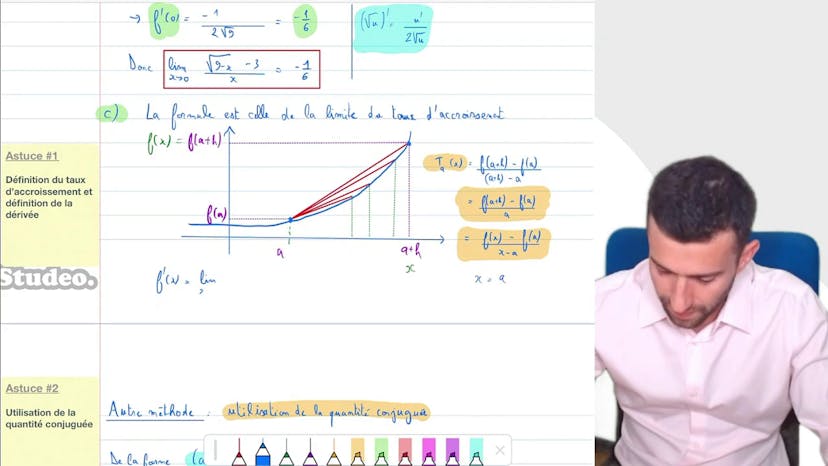
Utilisation de la dérivée
Dans ce cours, nous corrigeons un exercice sur les limites utilisant le taux d'accroissement et la dérivée. L'objectif est de se familiariser avec les limites qui sont un peu plus compliquées en utilisant la dérivée.
La première question demande d'utiliser la dérivée pour trouver la limite de la fonction f(x) = √(9 - x) quand x tend vers 0. Pour cela, nous utilisons la définition du taux d'accroissement et nous réécrivons la formule de la limite en utilisant la dérivée. En utilisant la définition de la dérivée, nous trouvons que la dérivée de f(x) est -1/(6√(9 - x)). Nous calculons ensuite la dérivée en x = 0 et trouvons que f'(0) = -1/6. Ainsi, la limite de √(9x) - 3/x quand x tend vers 0 est -1/6.
La deuxième question nous demande de trouver la limite de la fonction f(x) = √(2x - 1)/x en utilisant le même raisonnement. Nous posons f(x) = √(2x - 1) et trouvons que f'(x) = 1/(√(2x - 1)). En calculant f'(1.5), nous trouvons f'(1.5) = 1. Donc, la limite de √(2x - 1)/x quand x tend vers 0 est 1.
Enfin, la troisième question demande initialement de calculer la limite de e^x - 1 / x quand x tend vers 1. Cependant, il y a une erreur dans l'énoncé, car il devrait être e^(2x) - 1 / x. Ainsi, en


