 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths Spé
Analyse
Terminale

Intuition et déf
La vidéo traite de la convexité et commence par expliquer que l'on peut comprendre très simplement ce qu'est une fonction convexe ou concave avec l'aide d'un graphique. L'explication visuelle consiste à dire que convex c'est quand ça monte comme ça, et concave c'est quand ça monte mais pas trop vite. La vidéo introduit ensuite la définition mathématique officielle de la convexité, qui consiste à définir une séquente comme toute droite qui relie deux points d'une courbe, et une fonction convexe si, pour tout réel X de l'intervalle I, la courbe est en dessous de cette séquente. La vidéo explique que cette définition s'applique à toutes les fonctions, qu'elles soient continues ou pas. Enfin, la vidéo présente deux exemples de fonctions convexes et concaves, avec des graphiques pour illustrer ces concepts.
Maths Spé
Analyse
Terminale

Fonctions usuelles
Ce cours aborde les fonctions classiques comme la fonction racine et la fonction log. Les fonctions convexes sont celles qui ressemblent à un sourire, comme x² et exp x, tandis que les fonctions concaves ont une courbe en forme de sourire inversé, comme la fonction racine. La fonction 1 sur x est convexe sur r plus, mais concave sur r moins. Une règle hors programme, mais utile à retenir, est que les racines, comme la racine carrée, sont toujours concaves, tandis que les puissances supérieures strictes à 1 sont toujours convexes sur r plus. Les puissances de x peuvent être traçées pour illustrer cette règle.
Maths Spé
Analyse
Terminale

Inégalité fondamentale
Dans ce cours, nous apprenons la relation entre une fonction convex et ses séquentes. Pour être précis, nous étudions la différence d'ordonnée d'un point sur le segment bleu et d'un point sur la courbe rouge pour une même abscisse comprise entre l'abscisse de A et de B. Cette différence est plus grande lorsque le point est sur la courbe rouge que lorsqu'il est sur le segment bleu, ce qui montre que la fonction est convex. Nous nommons le point d'abscisse intermédiaire entre A et B "T" et prenons une moyenne pondérée des abscisses pour comparer l'image de ce point sur la courbe rouge à celle de l'équation du segment de la séquente. Nous démontrons ensuite que le lien entre la convexité et la concavité est réciproque. Une fonction convexe est moins concave et vice versa.
Maths Spé
Analyse
Terminale

Lien dérivation
La convexité d'une fonction dépend de la position entre la séquente et la courbe de la fonction, et non de la continuité ou de la dérivabilité de la fonction. Si f' est dérivable, on peut utiliser une autre définition de la convexité, qui est plus pratique pour les exercices, à savoir f' croissante pour une fonction convex, et f' décroissante pour une fonction concave. Pour une fonction deux fois dérivable, on peut étudier les variations de f'' pour connaître la convexité de la fonction. Si f'' est positive sur les zones où f' est positive, la courbe est convexe. Si f'' est négative sur ces zones, la fonction est concave. On n'a donc plus besoin de comparer la courbe et les droites pour étudier la convexité, mais il suffit de calculer la double dérivée.
Maths Spé
Analyse
Terminale
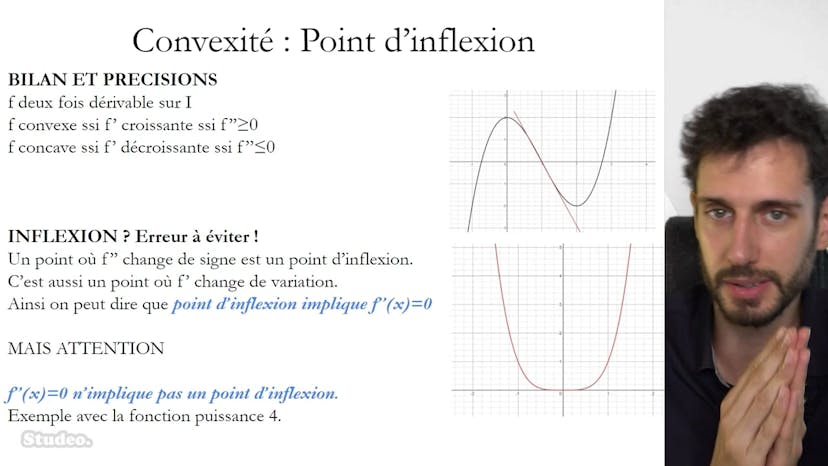
Point d'inflexion
Dans cette vidéo, le concept de point d'inflexion est présenté. Pour qu'un point A soit un point d'inflexion d'une fonction f en 2 fois dérivable, il faut que la courbe cf traverse la tangente TA en A. Cela se produit lorsque la dérivée seconde change de signe en A. Visuellement, on peut observer un changement de comportement entre concavité et convexité à ce point. De plus, le point d'inflexion correspond à un maximum en valeur absolue de la pente de la tangente en ce point. Il est important de noter que f'' de x égal à zéro n'implique pas nécessairement un point d'inflexion, cela dépend du comportement de la fonction autour de ce point.
Maths Spé
Analyse
Terminale

Déf fondamentale
Le logarithme, noté ln, est une fonction définie sur l'intervalle des nombres réels strictement positifs. Pour un nombre réel x strictement positif, ln(x) est l'unique solution de l'équation 2y = x. On peut définir le logarithme avec n'importe quel nombre x, en appelant la solution de l'équation 2y = x, ln(x). Les fonctions exponentielle et logarithme sont réciproques l'une de l'autre, ce qui signifie que la fonction exponentielle de ln(x) est égale à x, et que ln de la fonction exponentielle de x est égale à x. Cependant, ces fonctions ne sont pas définies de la même manière pour tous les x. Par exemple, le logarithme n'est défini que pour les x positifs stricts. Il est important de se rappeler que la racine carrée d'un carré est égale à la valeur absolue du nombre d'origine, et que la fonction logarithme et la fonction exponentielle sont réciproques l'une de l'autre.
Maths Spé
Probabilités
Terminale

Déterminer des ensembles
Dans ce cours sur le dénombrement, nous allons traiter des ensembles et des listes. La différence entre un ensemble et une liste est importante. Un ensemble est un sac qui contient des objets, sans ordre spécifique. Par contre, une liste est ordonnée. Pour représenter les ensembles, on utilise des accolades, tandis que les listes sont représentées entre parenthèses. Dans les exercices, il faudra toujours se demander si l'ordre compte (liste) ou non (ensemble). Dans les ensembles, lorsque l'ordre ne compte pas, on utilise des méthodes de combinatoire.
Dans l'exemple donné, les ensembles E et F contiennent respectivement les éléments H, E, I et D, I, E, R. Pour l'union de ces ensembles (E U F), on prend tous les éléments sans répétition, et on obtient H, E, I, D et R. Pour l'intersection de ces ensembles (E ∩ F), on cherche les éléments communs, et on obtient seulement E. Le produit cartésien (E × F) est l'ensemble de toutes les paires d'éléments des deux ensembles, où l'ordre compte. Dans cet exemple, les paires possibles sont H D, H I, H E, H R, etc.
Une paire est un ensemble de deux éléments. On peut former les paires possibles à partir d'un ensemble contenant trois éléments, ce qui donne les paires H E, H I et E I.
Il est important de faire la distinction entre un ensemble et une liste pour compter les possibilités. N'hésitez pas à poser des questions si besoin.
Maths Spé
Probabilités
Terminale

Utiliser un diagramme
Les diagrammes sont un outil utile pour la compréhension visuelle des informations. Dans cet exemple, nous avons une station de sport d'hiver avec 20 touristes. Parmi eux, 14 pratiquent le ski de piste, 7 le ski de fond, et 4 pratiquent les deux activités.
En utilisant un diagramme, nous plaçons les 20 touristes dans une bulle bleue. Dans cette bulle, 10 personnes pratiquent uniquement le ski de piste, 4 pratiquent à la fois le ski de piste et le ski de fond, et 3 pratiquent uniquement le ski de fond. En ajoutant ces chiffres (10 + 4 + 3), nous obtenons bien les 7 personnes qui pratiquent le ski de fond au total.
Pour déterminer combien de touristes ne pratiquent aucune des activités, nous comptons simplement le nombre de personnes qui pratiquent une activité (10 + 4 + 3), puis soustrayons ce total du nombre total de touristes (20 - 17). Ainsi, nous découvrons qu'il y a 3 touristes qui ne pratiquent aucune des activités.
Dans des exemples plus complexes, le principe reste le même : placer des bulles représentant différentes catégories et compter pour obtenir des chiffres précis. Les diagrammes sont donc un outil très utile pour comprendre et analyser des données.
Maths Spé
Probabilités
Terminale

Dénombrer des ensembles simples
Ce cours présente des exemples de dénombrement. Dans le premier exemple, on doit déterminer le nombre de résultats possibles pour lancer une pièce 7 fois de suite. En se posant les questions « est-ce que c'est une liste ou un ensemble? » et « est-ce que l'ordre compte? », on conclut que l'ordre compte et qu'on peut répéter les résultats. Ainsi, le nombre de tirages possibles est de 2 puissance 7.Dans le deuxième exemple, on doit déterminer le nombre de distributions possibles pour deux joueurs de domino recevant 7 dominos chacun parmi les 28 dominos du jeu. En considérant que l'ordre compte, le nombre de listes possibles est de 28 x 27 x 26 ... x 15 x 14. Une autre façon d'exprimer cela est 28! sur 14!.Dans le dernier exemple, on dispose de 4 gâteaux et 4 invités, et il faut attribuer un gâteau à chaque invité. Avec l'ordre compte et sans répétition, le nombre de façons de procéder est de 4!.Pour dénombrer, il faut se poser les questions « est-ce que j'ai l'ordre compte ou ne compte pas? » et « est-ce que je peux avoir répétition? ».
Maths Spé
Probabilités
Terminale

Tirage successif sans remise
Dans ce cours, nous abordons le concept de tirage successif sans remise. L'énoncé nous donne un exemple concret : nous avons 5 élèves qui se tiennent en rang et nous voulons savoir combien il y a de façons de les ranger. Pour résoudre ce problème, nous devons d'abord nous poser quelques questions. Est-ce une liste ou un ensemble ? Y a-t-il des répétitions possibles ?
Dans ce cas, il s'agit d'une liste car l'ordre compte. Par exemple, l'ordre "1, 2, 3, 4, 5" est différent de "5, 4, 3". De plus, il n'y a pas de répétition possible car nous ne pouvons pas avoir deux fois le même élève à la même position.
Maintenant que nous avons clarifié ces points, la résolution devient assez simple. Pour la première position, nous avons 5 choix possibles. Pour la deuxième position, une fois que nous avons placé quelqu'un, nous n'avons plus que 4 choix. Et ainsi de suite, jusqu'à la dernière position où nous n'avons plus qu'un seul choix. Nous multiplions donc ces choix successifs : 5 x 4 x 3 x 2 x 1, ce qui est égal à 5!.
Cette formule générale s'applique également lorsque nous avons P tirages successifs sans remise dans un ensemble à N éléments. Nous pouvons l'exprimer comme suit : N! sur N-P!.
En résumé, pour résoudre le problème des tirages successifs sans remise, nous utilisons la formule N! sur N-P!.
Révisions Maths lycée
Probas Terminale
MPSI/PCSI

Principe multiplicatif
Dans cet exercice sur les échanges de poignées de mains entre deux équipes de 15 personnes, on cherche à déterminer le nombre de poignées de mains échangées. Pour résoudre ce problème, il faut analyser la notion de poignée de main en tant que lien entre deux personnes appartenant à des équipes différentes. On peut donc former une paire en choisissant une personne de l'équipe 1 et une personne de l'équipe 2. Il y a 15 possibilités dans l'équipe 1 et 12 possibilités dans l'équipe 2, ce qui donne un total de 180 poignées de mains possibles. Il est important de noter que chaque poignée de main est comptée une seule fois, car on a établi une liste où le premier élément vient de l'équipe 1 et le second élément vient de l'équipe 2. Ainsi, on évite de compter deux fois la même paire en inversant les rôles des équipes. En comprenant qu'il s'agit de compter des paires, le problème devient plus simple à résoudre.
Maths Spé
Probabilités
Terminale
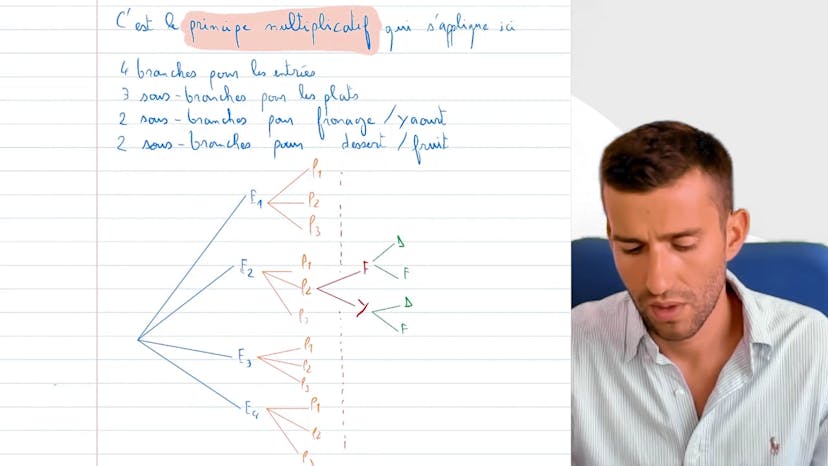
Principe multiplicatif et arbre pondéré
Apprendre à faire un arbre pondéré peut être pratique, mais cela peut prendre du temps. Si vous avez trop de sous-branches, il peut ne plus être nécessaire de faire un arbre pondéré. Au début, il est préférable de faire un brouillon de l'arbre pour clarifier les idées. Par exemple, si une cantine scolaire offre 4 entrées, 3 plats, et le choix entre fromage ou yaourt, et dessert ou fruit, il serait possible de faire un arbre pondéré. Cependant, cela peut devenir assez volumineux. Pour compter, le principe multiplicatif s'applique en faisant une multiplication de chaque possibilité. Pour le moment, il n'est pas nécessaire de se préoccuper des pondérations, mais cela sera abordé dans le chapitre suivant avec les probabilités.


