Cours d'apprentissage en ligne

Plein de limites !

Dans ce cours sur les limites en mathématiques, nous apprenons deux méthodes principales pour les gérer : la méthode du terme dominant et la méthode de l'encadrement. La première consiste à comparer les termes dominants au numérateur et au dénominateur d'une fraction pour avoir une intuition de ce qui se passera lorsque n devient très grand. La seconde méthode nous permet d'utiliser le théorème d'encadrement en encadrant les éléments dans une question sur les limites de suite contenant des fonctions trigonométriques. Le cours nous enseigne comment factoriser le terme dominant pour répondre à la question en haut et en bas, et comment utiliser le théorème des gendarmes pour des limites finies encadrées des deux côtés. Des exemples sont donnés pour illustrer les méthodes, et nous apprenons également comment utiliser la comparaison de puissance pour répondre aux limites géométriques.

Téléscopage !

Le cours traite de la détermination de limites de suites définies comme des sommes de termes d'autres suites. Le premier exercice consiste à déterminer la limite de la suite Un, qui est 1/n, qui tend vers 0. Ensuite, l'exercice suivant montre que pour toutes les n appartenant à N, Un égale à 1/(n-1) - 1/n+1. La difficulté de cet exercice est de ne pas recopier la réponse et de partir de l'équation donnée pour démontrer qu'elle est égale à Un. Le troisième exercice consiste à calculer la somme de la suite. En utilisant la question précédente, on peut simplifier l'expression de Un en une somme télescopique, où les termes successifs se dégagent mutuellement, laissant seulement Un et Un+1. Finalement, on obtient que la somme tend vers 1.

Majoration astucieuse

Le cours concerne l'étude des variations et la convergence d'une suite mathématique donnée sous la forme d'un quotient, Vn = (6n + 3)/(n + 1). La méthode classique consiste à utiliser le critère de croissance en comparant Vn+1/Vn à 1 pour montrer que la suite est croissante et à démontrer qu'elle est bornée par 6 pour déduire qu'elle converge grâce au théorème de convergence monotone. Une autre méthode consiste à travailler sur l'expression de Vn en écrivant Vn = (6n + 1 - 3)/(n + 1) = ((6n + 1)/(n + 1)) - (3/(n + 1)) pour montrer que la suite est croissante et bornée par 6, et pour obtenir directement la limite de la suite qui est 6. L'analyse mathématique de cette suite est utilisée pour illustrer différentes méthodes et stratégies de résolution de problèmes en mathématiques.

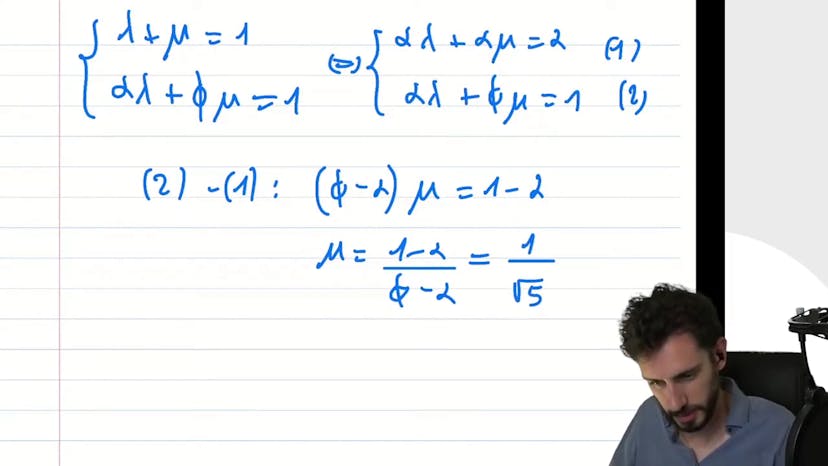
Prépa : Fibonacci

La suite de Fibonacci et le nombre d'or sont définis par récurrence avec chaque terme étant la somme des deux précédents. Pour exprimer chaque terme de la suite comme une combinaison linéaire de sommes géométriques, il faut trouver des réels a, b, lambda et mu qui vérifient une certaine relation de récurrence. Au lieu de résoudre directement les équations impliquant les quatre variables, on peut chercher s'il existe uniquement une somme géométrique qui fonctionne, ce qui mène à deux valeurs potentielles pour la raison de la suite géométrique. En utilisant cela, on peut aboutir à une expression simple pour chaque terme de la suite de Fibonacci en fonction du nombre d'or et de certains coefficients. En analysant les raisons de la suite géométrique, on peut montrer que la suite de Fibonacci converge vers le nombre d'or.

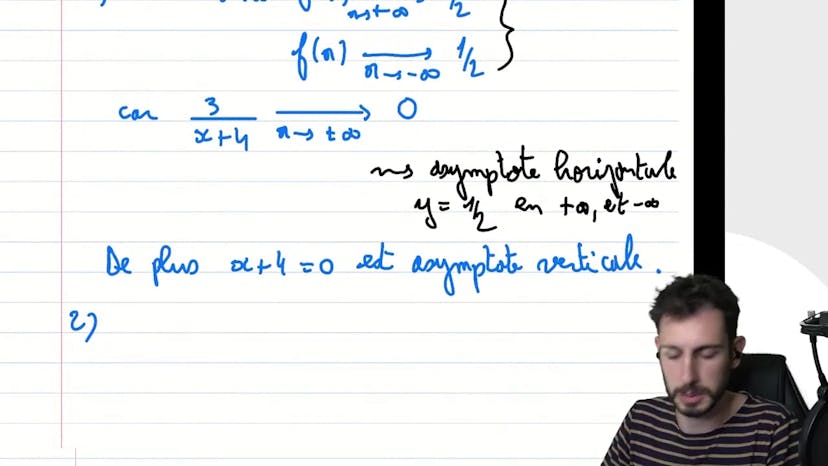
Asymptote et position relative

En étudiant une fonction classique, l'exercice porte sur l'étude de position relative et des asymptotes. Le réflexe immédiat est de factoriser f2x en bas par 2xx plus 4. Pour trouver la limite en plus et moins à l'infini, on peut considérer que pour des valeurs très élevées de x, une constante n'affecte pas grand-chose. Ainsi, f2x est approximativement égal à x sur 2x, ce qui fait 1,5. Ensuite, on peut réécrire la fonction homographique avec un polynôme de degré 1 pour le numérateur et le dénominateur. Il est utile de bien connaître cette technique pour trouver les éléments clés du comportement asymptotique. En utilisant cette écriture, on peut trouver les deux asymptotes de la fonction et résoudre la question 1. Pour la question 2, il faut trouver la position relative de CF par rapport à l'asymptote horizontale en faisant la différence des expressions de la fonction et de l'asymptote. En résumé, il est important de savoir reconnaître rapidement les asymptotes et de connaître la technique pour réécrire une fonction homographique.

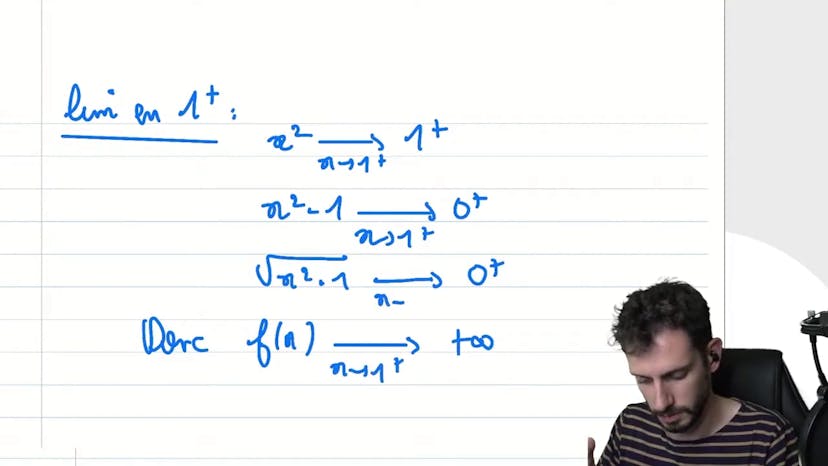
Étude TRES complète

Ce cours traite de la résolution d'une expression complexe en mathématiques. Pour trouver les valeurs de f, il est important de garder une expression positive ou nulle sous la racine, et d'éviter les divisions par zéro. Il est conseillé de vérifier la parité de la fonction afin de simplifier les calculs. En utilisant cette méthode, il est possible de trouver les limites de la fonction, en se basant sur l'infini et les bornes de DF. Les asymptotes sont également déterminées, en utilisant les limites précédemment calculées.

Asymptote oblique

En résumé, l'asymptote oblique est une droite de la forme AX plus B qui est approchée plus ou moins à l'infini. Bien que hors programme, il est important d'essayer les exercices qui impliquent des asymptotes obliques car il peut être difficile de les résoudre en terminale. La simplification en fractions est cruciale pour simplifier les expressions. Pour la dérivabilité d'une fonction, si elle n'a pas de racines ou de valeur absolue, alors elle est dérivable. Pour l'étude des variations et limites d'une fonction, il faut calculer les limites au bord de l'intervalle, vérifier la parité de la fonction et la dérivée. L'analyse de la position relative entre deux expressions est l'analyse du signe de la différence entre les deux expressions, qui doit être vérifiée pour l'étude de la position relative.

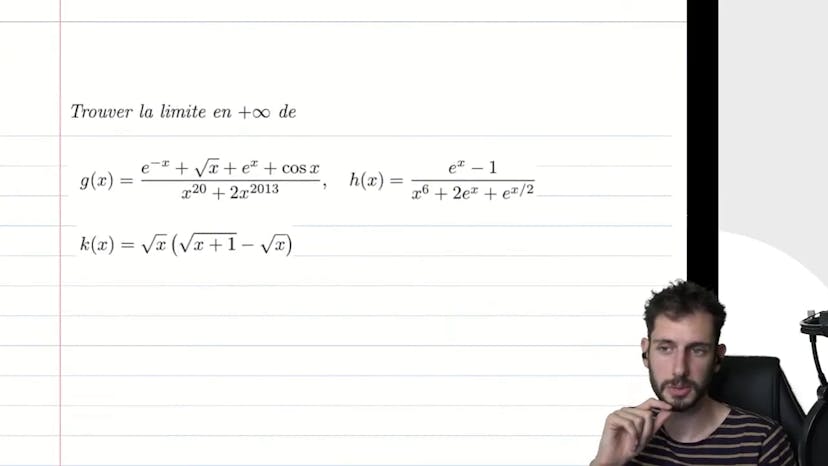
Croissance comparée plus lourde

Ce cours explique comment utiliser la croissance comparée pour trouver le petit h de x en gros. Pour simplifier, on compare E de x avec n'importe quelle puissance, en mettant en facteur E de x. On obtient 1-E de x, qui est facile à gérer. L'exercice tend vers 0 quand x tend vers l'infini, avec quelques nuances à prendre en compte. En résumé, ce cours montre une méthode utile pour trouver le terme dominant en mathématiques.

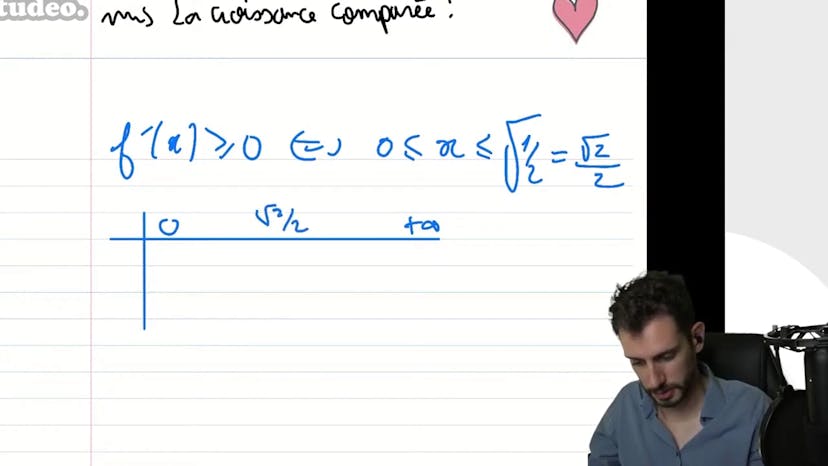
Difficile : BAC 2009

En bref, ce cours porte sur l'étude de fonction complète d'un examen de mathématiques de 2009. Il faut d'abord trouver la limite de la fonction à l'infini, ce qui nécessite l'utilisation de la croissance comparée pour comparer l'exponential et les puissances de x. Ensuite, il faut montrer que la fonction admet un maximum, ce qui nécessite de calculer la dérivée et d'analyser ses changements de signe. Enfin, on peut déterminer la valeur de la fonction au maximum, qui est égale à racine de 2 sur 2 fois exponentielle de moins 1 sur 2.

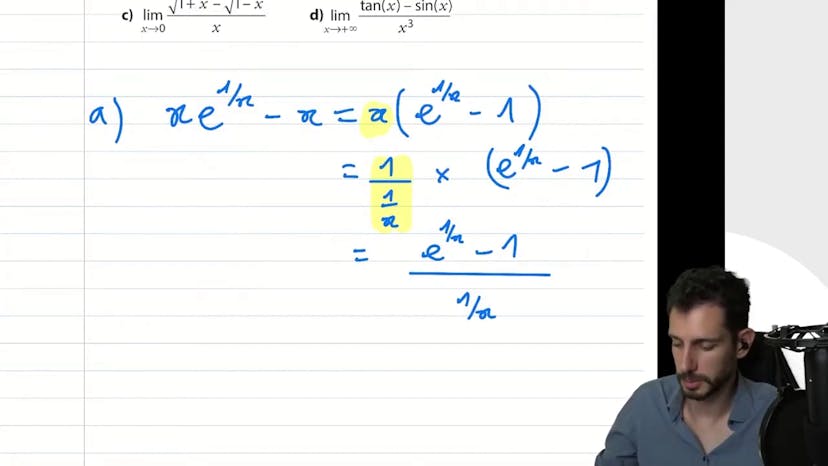
Encore un taux d'accroissement de exp

Dans cette vidéo, le professeur résout un problème de limite mathématique. Il étudie la fonction x exponentiel 1 sur x, moins x, en plus infini. En utilisant des techniques de factoring et de taux d'accroissement, il parvient à simplifier la fonction et à trouver sa limite quand x tend vers plus infini, qui s'avère être 1. Le professeur souligne que des problèmes similaires peuvent être encore plus compliqués et nécessiteront de solides connaissances en mathématiques pour être résolus.

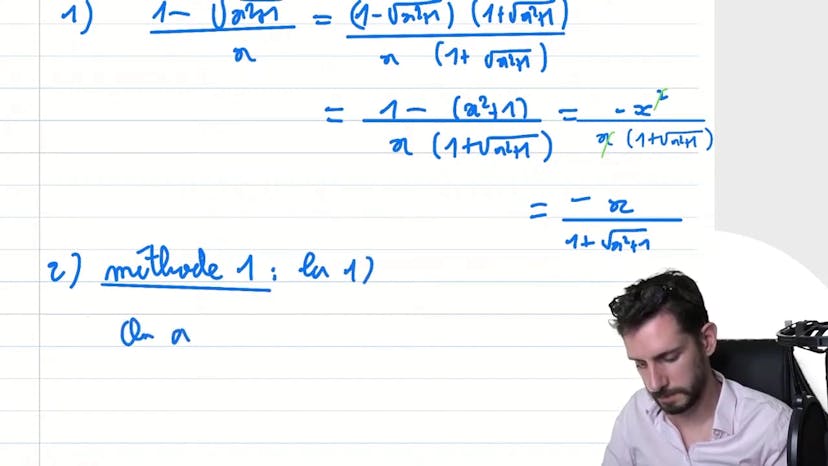
Saut de continuité

En résumé, ce cours traite de la continuité d'une fonction définie par f(x) = 2x si x est différent de 0, et f(z) = m sinon. Le premier exercice consiste à déterminer si cette fonction est continue. Deux méthodes sont proposées pour résoudre cet exercice : la première consiste à utiliser la quantité conjuguée pour simplifier la fonction et trouver la limite, tandis que la deuxième consiste à reconnaître un taux d'accroissement et utiliser la dérivabilité de la fonction racine pour trouver la limite. Le deuxième exercice demande de trouver la valeur de m pour que la fonction soit continue en 0, en utilisant la définition fondamentale de la continuité. La réponse est m = 0.