 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths SM&SP
Analyse
2BAC SM Maroc

Théorème de Rolle
Bienvenue à tous ! Dans ce cours, nous allons voir comment bien utiliser le théorème de Rolle en SEO friendly.
Le théorème de Rolle est utilisé lorsque l'on souhaite montrer que la dérivée d'une fonction s'annule au moins une fois sur un intervalle donné.
Pour cela, on considère une fonction f définie sur un intervalle i, de classe Cn, et qui s'annule en n plus un point distinct de i.
La première méthode pour démontrer cela est par récurrence. On montre ainsi que la dérivée km s'annule n plus une moins k fois au moins sur i.
Dans cette démonstration, on applique le théorème de Rolle sur des intervalles spécifiques, ce qui permet de montrer que la dérivée s'annule au moins une fois sur ces intervalles.
On peut continuer ainsi jusqu'à obtenir que la dérivée enième de f s'annule au moins une fois.
Dans la seconde partie du cours, on aborde une astuce un peu plus complexe. On pose une fonction h qui est le produit de f par l'exponentielle de alpha x.
En dérivant cette fonction, on obtient f' + alpha f fois l'exponentielle de alpha x.
L'astuce ici est que, comme l'exponentielle est toujours positive, si h s'annule au moins une fois, cela signifie que le terme f' + alpha f s'annule lui aussi au moins une fois.
Ainsi, on peut appliquer le théorème de Rolle sur h prime et montrer que la dérivée enième de f' + alpha f s'annule au moins une fois.
Voilà comment bien utiliser le théorème de Rolle dans des exercices, en utilisant ces petites astuces pour démontrer que les dérivées s'annulent sur les intervalles donnés.
Maths SM&SP
Analyse
2BAC SM Maroc

Formule de Taylor Lagrange
Dans ce cours, nous allons étudier le concept de point fixe en mathématiques. Un point fixe est une solution de l'équation f(x) = x, où f est une fonction dérivable sur un intervalle ab. Pour qu'un point fixe existe et soit unique, il faut que la dérivée de f soit inférieure en valeur absolue à une constante k appartenant à (0,1).
Pour prouver l'existence d'un point fixe, nous utilisons un résultat classique en mathématiques. Nous posons g(x) = f(x) - x et nous montrons que g(a) > 0 et g(b) < 0, où a et b sont les bornes de l'intervalle ab. En utilisant le théorème des valeurs intermédiaires, nous concluons qu'il existe au moins un point fixe gamma tel que g(gamma) = 0.
Ensuite, nous démontrons l'unicité du point fixe. Supposons qu'il existe deux points fixes gamma1 et gamma2 distincts. En utilisant le théorème des inégalités des accroissements finis, nous montrons que la différence entre gamma1 et gamma2 est strictement inférieure à gamma1 - gamma2, ce qui est impossible. Donc, nous concluons que gamma1 = gamma2, c'est-à-dire qu'il n'existe qu'un seul point fixe.
Enfin, nous étudions la convergence vers le point fixe. Nous considérons une suite u(n) définie par récurrence, avec u(0) dans l'intervalle ab, et nous montrons que |u(n) - gamma| est inférieure à k^n |u(0) - gamma|. Puisque k est strictement inférieur à 1 en valeur absolue, la suite u(n) converge vers le point fixe gamma.
Pour mieux comprendre le caractère attractif du point fixe, nous utilisons des graphiques. Si la pente de la fonction f est inférieure à 1 sur tout l'intervalle ab, alors la suite u(n) converge rapidement vers le point fixe. Si la pente est supérieure à 1, la suite fuirait plutôt le point fixe.
En conclusion, le théorème du point fixe est un résultat classique en mathématiques et peut être utilisé pour résoudre des exercices et des problèmes. Il permet de démontrer l'existence, l'unicité et la convergence des points fixes d'une fonction dérivable.
Maths SM&SP
Analyse
2BAC SM Maroc

Règle de l’Hopital
Dans cette vidéo, on aborde la règle de l'hôpital, un théorème intéressant mais qui n'est pas enseigné dans le programme français. Cependant, dans d'autres pays comme l'Angleterre et le Luxembourg, il est au programme de terminale. Ce théorème s'applique lorsque l'on a deux fonctions f et g continues et dérivables sur un intervalle a, b. On suppose qu'il existe un point x0 où les deux fonctions s'annulent, et que la dérivée de g ne s'annule pas ailleurs dans cet intervalle. La règle de l'hôpital affirme que si la limite de f' sur g' quand x tend vers 0 tend vers l, alors la limite de f sur g quand x tend vers 0 tend vers l également.
Pour démontrer ce théorème, on utilise le théorème des accroissements finis généralisé, qui lui est au programme. On crée une fonction h qui est égale à une expression comprenant les fonctions f et g. En calculant sa dérivée, on peut montrer que ce théorème s'applique. On utilise alors ce théorème dans deux exemples spécifiques pour montrer l'efficacité de la règle de l'hôpital.
En résumé, la règle de l'hôpital est un théorème qui permet de calculer des limites de fonctions indéterminées. Bien que ce théorème ne fasse pas partie du programme français, il peut être appliqué dans des exercices pour simplifier les calculs.
Maths SM&SP
Analyse
2BAC SM Maroc

Polynome de Legendre
Les polynômes de Legendre sont une famille de polynômes qui se présentent sous la forme Pn(x) = (d^n/dx^n)(x^2-1)^n. Ils sont étudiés dans le contexte des dérivés et ont un degré de 2n avec un coefficient dominant de 2n! / n!. Les racines de ces polynômes sont étudiées en utilisant le théorème de Rolle, qui montre que les racines sont distinctes et se situent entre -1 et 1. Cette propriété permet de conclure que les polynômes de Legendre ont n racines distinctes. Les polynômes de Legendre sont souvent rencontrés dans le chapitre sur les polynômes et leur forme doit être retenue car elle revient souvent.
Maths SM&SP
Analyse
2BAC SM Maroc
Corde et tangente
Bonjour à tous ! Aujourd'hui, nous allons aborder la méthode des cordes et des tangentes dans le cadre de fonctions. Nous découvrirons que dans certaines conditions, il est possible de trouver une tangente et une corde communes. L'exercice que nous allons traiter propose une fonction vérifiant plusieurs caractéristiques : elle est définie de 0 à 1 dans R, est de classe c1 et vérifie f(0) = f'(0) = f'(1) = 0. Notre objectif est de montrer qu'il existe un point c appartenant à l'intervalle [0,1] tel que f'(c) = f(c)/c.
Pour commencer, nous devons comprendre ce que cela représente géométriquement. Si nous prenons un élément c dans l'intervalle [0,1] et le point m sur la courbe correspondant à ce c, nous devons rappeler l'équation de la tangente en ce point ainsi que celle de la corde reliant le point (0,f(0)) au point (c,f(c)). Notre but est de donner une interprétation géométrique de ce résultat.
En général, la corde entre les points m et o (0,f(0)) correspond à la droite verte dans notre dessin, tandis que la tangente est la droite passant par le point m et ayant une pente égale à la dérivée de la fonction en ce point. Donc, les pentes de ces droites sont respectivement f'(c) pour la tangente et f(c)/c pour la corde (dans le cas où f(0) = 0).
Notre objectif est de trouver un point où la corde et la tangente se confondent, c'est-à-dire où ces deux droites passent par le même point et ont la même pente. En d'autres termes, nous cherchons un point où la corde et la tangente coïncident.
Maintenant que nous comprenons cela, examinons les équations de la tangente et de la corde. L'équation de la tangente est y = f'(c)*(x-c) + f(c), tandis que l'équation de la corde est y = f(c)/c * x. Si nous simplifions ces expressions, nous obtenons les formes ax + b, avec a et b correspondant aux coefficients directs et à l'ordonnée à l'origine respectivement.
Pour que ces deux droites soient égales, elles doivent avoir les mêmes coefficients directs et les mêmes ordonnées à l'origine. Ainsi, ces deux équations aboutissent à la condition suivante : f'(c) = f(c)/c. C'est ce que nous cherchons à prouver.
Dans notre dessin, nous avons choisi les bonnes caractéristiques : f(0) = 0, f'(1) = 0 et f'(0) = 0. Le point c que nous cherchons se trouve ici, où la tangente et la corde se confondent.
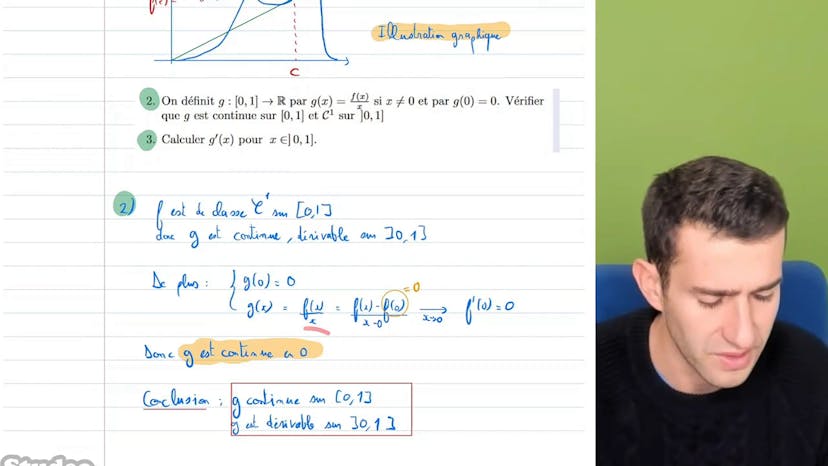
Pour continuer, nous introduisons une fonction auxiliaire f(x)/x et nous devons montrer qu'elle est continue sur l'intervalle [0,1] et de classe c1 sur l'intervalle ouvert (0,1). Comme f est de classe c1 sur [0,1], elle l'est également sur (0,1) en faisant attention au problème en 0 dû à la division par x. En posant g(0) = 0, nous vérifions sa continuité en 0. En dehors de 0, il n'y a aucun problème pour la continuité.
La question suivante consiste à calculer g'(x) pour tout x dans (0,1). Nous utilisons les théorèmes de dérivation classiques pour calculer g'(x) = f'(x) - f(x)/x^2.
Nous avons alors deux cas à examiner : lorsque f(1) = 0 et lorsque f(1) > 0. Dans le premier cas, c=1 convient car f(c) = f(1) = 0 et f'(c) = f'(1) = 0, ce qui satisfait notre équation recherchée f'(c) = f(c)/c.
Dans le second cas, nous devons calculer g(0), g(1) et g'(1). Nous avons g(0) = 0, g(1) = f(1)/1 > 0 et g'(1) = -f(1) < 0. Nous en déduisons que g' s'annule sur [0,1]. En appliquant le théorème de Rolle sur g', nous trouvons qu'il existe un c entre 0 et 1 tel que g'(c) = 0. En reprenant notre calcul de g'(x), nous obtenons l'équation recherchée f'(c) = f(c)/c.
En conclusion, nous avons répondu au problème en prenant en compte les hypothèses suivantes : f(0) = f'(0) = f'(1) = 0. Dans ce cas, nous avons pu montrer qu'il existe un point c où la corde et la tangente sont confondues.
C'est ainsi que se conclut cet exercice.
Maths
Algèbre
MPSI/PCSI

Carré parfait
Dans cet exercice, nous souhaitons démontrer que le produit de 4 entiers consécutifs augmentés de 1 est un carré parfait. Pour ce faire, nous allons réécrire cette consigne de manière algébrique. Nous posons le but de montrer l'existence d'un cas appartenant à n, un entier naturel, tel que le produit des 4 entiers consécutifs (n x (n+1) x (n+2) x (n+3)), augmenté de 1, est égal à k², où k est un autre nombre au carré.
En développant cette expression, nous obtenons n⁴ + 6n³ + 11n² + 6n + 1, qui contient 5 termes. Sachant qu'une forme de carré parfait a au plus 3 termes après simplification, nous pouvons conclure que ce n'est pas le cas ici. Cependant, nous explorons la possibilité que certains de ces 5 termes soient en réalité 2 termes regroupés. Par exemple, 6n³ pourrait être équivalent à 2n³ + 4n³, de même pour 5n² et 6n².
Nous remarquons que ces 5 termes peuvent être écrits comme une triple somme au carré. En identifiant les termes, nous trouvons que le plus grand degré est n⁴, que nous associons à a² (a étant égal à n²). Le plus petit degré, équivalent à c², est 1, ce qui signifie que c est égal à 1.
Maintenant, nous cherchons à identifier les termes avec b. Nous constatons que 6n³ peut être exprimé comme 2ab. Si nous avions choisi 2bc, nous aurions trouvé b = 3n³, ce qui n'est pas possible car n² est le plus grand degré.
Finalement, nous trouvons que b est égal à 3n.
En réécrivant l'expression initiale en utilisant ces identifications, nous obtenons que le produit des 4 entiers consécutifs augmentés de 1 est égal à (n² + 3n + 1)², ce qui est bien un carré parfait.
Maths
Algèbre
MPSI/PCSI

Divisibilité
Dans cet exercice, on démontre deux résultats arithmétiques. Tout d'abord, pour tout entier n, on montre que 6 divise 5^n + n. En utilisant les congruences, on montre que ce nombre est divisible par 2 et par 3, donc par 6. Ensuite, on démontre que pour tout entier n, 4^(2^n) + 2^(2^n) + 1 est divisible par 7. En examinant les premières valeurs de n, on constate un motif (4, 2, 4, 2...) qui nous permet de généraliser la propriété par récurrence. Finalement, on conclut en affirmant que pour tout entier n, ces deux propriétés sont vérifiées.
Maths
Algèbre
MPSI/PCSI

Division euclidienne
Dans cet exercice, on nous demande de déterminer le reste de la division du nombre 96 842 par chacun des nombres 256 et 375. Pour cela, nous utilisons le calcul initial qui nous donne le résultat 96 842 = 256 x 375 + 842. Notons que le reste dans une division euclidienne doit être strictement plus petit que le quotient. Cependant, dans ce cas, 842 n'est pas plus petit que 256 ou 375, ce qui pose problème.
Pour résoudre ce problème, nous allons réduire uniquement le chiffre 842. La méthode consiste à faire la division euclidienne de 842 par 256 pour obtenir le quotient 3 et le reste 74. Ensuite, nous faisons la division euclidienne de 842 par 375 pour obtenir le quotient 2 et le reste 92. Cette fois-ci, les conditions de la division euclidienne sont respectées, c'est-à-dire que le reste est plus petit que le quotient dans les deux cas.
Nous utilisons ensuite ces résultats pour réécrire l'équation initiale. Ainsi, 96 842 devient 256 x 375 + 375 x 2 + 92. Nous factorisons ces termes par 375 pour obtenir 375 x 258 + 92. Cette nouvelle écriture respecte bien la division euclidienne, car le reste 92 est plus petit que 375.
En utilisant la même méthode, en réécrivant l'équation en utilisant cette fois-ci l'écriture pour 842, nous trouvons que 96 842 est égal à 256 x 378 + 74. Le nombre 378 est obtenu en ajoutant 3 fois 256 à 375.
Ainsi, le reste de la division euclidienne de 96 842 par 375 est 92, et le reste de la division euclidienne de 96 842 par 256 est 74.
Maths
Algèbre
MPSI/PCSI

Ecriture en base
Dans cet exercice, on cherche à démontrer l'existence et l'unicité d'une base B telle que tout entier naturel n puisse être décomposé de manière unique sous la forme d'une somme de coefficients multipliés par des puissances de B.
Pour démontrer l'existence, on utilise une récurrence forte. On suppose que la propriété P(n) est vraie pour tout entier k plus petit que n, et on montre que P(n+1) est aussi vraie. On distingue deux cas : si n+1 est strictement plus petit que B, alors n+1 peut être écrit sous la forme d'une somme avec un seul coefficient, qui est n+1 lui-même. Si n+1 est supérieur ou égal à B, on utilise la division euclidienne pour écrire n+1 sous la forme de BQ + R, où Q est plus petit que n et R est entre 0 et B-1. On utilise ensuite l'hypothèse de ré
Maths
Algèbre
MPSI/PCSI
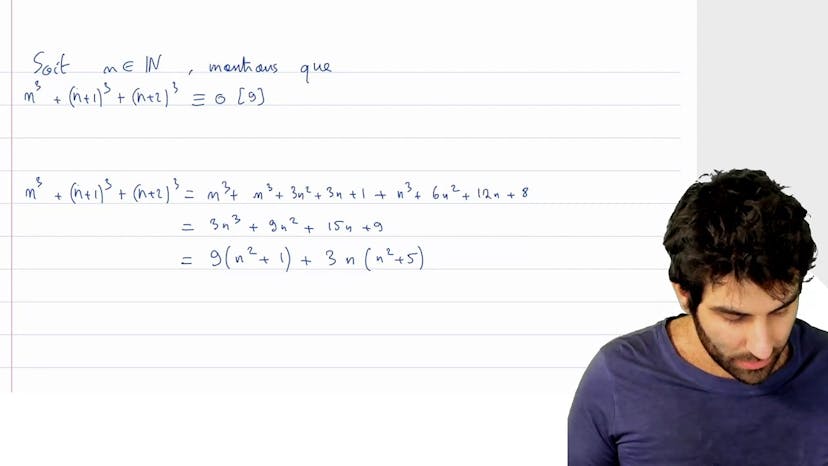
Cubes consécutifs
Dans cet exercice, on démontre que la somme de 3 cubes consécutifs est toujours divisible par 9. Pour cela, on utilise les congruences pour simplifier les résultats. On veut montrer que la somme de 3 cubes consécutifs, soit n^3 + (n+1)^3 + (n+2)^3, est congru à 0 modulo 9.
En développant cette expression, on obtient 3n^3 + 9n^2 + 15n + 9. On regroupe les termes pour faciliter les calculs et remarquons que le premier terme est déjà divisible par 9.
En factorisant le deuxième terme par 3n et le troisième terme par 3, on obtient 9(n^2 + 1)(3n + 5).
Il est facile de voir que le terme 9(n^2 +1) est congru à 0 modulo 9 car il est divisible par 9. De plus, le terme 3n + 5 est congru à 0 modulo 3 car il est divisible par 3.
Ainsi, nous avons démontré que pour tout n, la somme de 3 cubes consécutifs est divisible par 9.
Maths
Algèbre
MPSI/PCSI

Congruences avec les puissances
Dans cet exercice, l'objectif est de trouver le reste de la division par 13 du nombre 100 puissance 1000. Pour cela, il est recommandé d'utiliser les congruences plutôt qu'une calculatrice en raison de la taille du nombre.
Tout d'abord, on détermine le reste de la division de 100 par 13, qui est 9. Ensuite, au lieu de travailler avec 100, on travaillera avec 9 car ils sont congruents modulo 13. Par exemple, si 100 puissance 4 est congru à 1 modulo 13, alors 9 puissance 4 sera aussi congru à 1 modulo 13.
On calcule donc les puissances de 9. On constate que 9 puissance 2 est congru à 3 modulo 13, mais ce n'est pas ce que l'on souhaite. On cherche à trouver une puissance de 9 qui est congru à 1 modulo 13, et on trouve que 9 puissance 3 est congru à 1 modulo 13. Donc la puissance recherchée est 3.
On réécrit alors 100 puissance 3 comme congru à 9 puissance 3, qui est congru à 1 modulo 13. Etant donné que 100 puissance 3 est congru à 1 modulo 13, le nouveau diviseur sera 3 cette fois-ci. On effectue donc une division euclidienne de 1000 par 3, ce qui donne 333 avec un reste de 1.
On réécrit alors 100 puissance 1000 comme 100 puissance 3 fois 333 plus 1, en utilisant les règles de calcul sur les puissances. Cela devient donc (100 puissance 3) puissance 333 multiplié par 100.
Il est important de ne pas se tromper en interprétant cela comme (100 puissance 333) puissance 3, car cela engendrerait une interprétation différente. Ici, on écrit cette expression de cette façon spécifique car on sait que 100 puissance 3 est congru à 1 modulo 13, et que 100 est congru à 9. Ainsi, on peut remplacer 100 par 9 dans l'expression.
En considérant que 1 puissance 333 est égal à 1 modulo 13, le calcul final donne que 1 puissance 333 fois 9 est congru à 9 modulo 13. Par conséquent, selon la définition des congruences, le reste de la division euclidienne de 100 puissance 1000 par 13 est égal à 9.
Maths
Algèbre
MPSI/PCSI
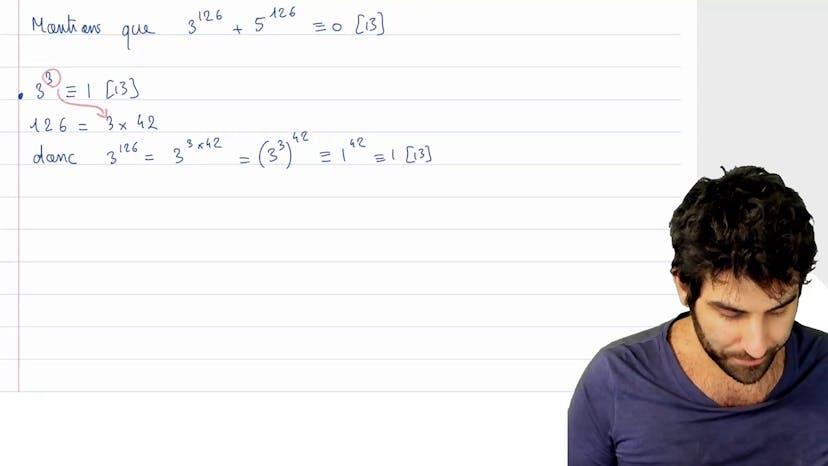
Division de puissances
Dans cet exercice, nous allons montrer que 13 divise 3^126 + 5^126 en utilisant les congruences. Au lieu de montrer que chaque terme est congru à 0 modulo 13, nous allons examiner à quoi chaque terme est congru modulo 13.
Pour cela, nous cherchons d'abord une puissance de 3 qui est congrue à 1 modulo 13. Nous trouvons que 3^3 ≡ 1 modulo 13. Ensuite, nous divisons 126 par 3 pour obtenir 42 sans reste. Ainsi, 3^126 = (3^3)^42 ≡ 1^42 ≡ 1 modulo 13.
De la même manière, nous cherchons une puissance de 5 qui convient. Nous trouvons que 5^3 ≡ 8 modulo 13. Ensuite, nous divisons 126 par 4 pour obtenir 31 avec un reste de 2. Ainsi, 5^126 = (5^4)^31 * 5^2 ≡ 1^31 * 12 ≡ 12 modulo 13.
Finalement, nous avons montré que 3^126 ≡ 1 modulo 13 et 5^126 ≡ 12 modulo 13. Donc, 3^126 + 5^126 ≡ 1 + 12 ≡ 0 modulo 13. Ainsi, nous concluons que 13 divise bien 3^126 + 5^126.


