Cours d'apprentissage en ligne

Tentative d'expliciter une suite récurrente

Ce cours traite de la recherche d'une valeur initiale U0 pour une suite mathématique qui sera constante ou arithmétique. Si Une suite est constante, cela signifie que pour tout entier n, Un+1 = Un = U0. En résolvant l'équation U0/(10/7-U0) = U0, nous trouvons que deux valeurs pour U0 donnent une suite constante: 2 et 5. Si une suite est arithmétique, alors Un = U0 + nR, où R est la différence constante entre les termes. En utilisant la notion de limites, nous trouvons que si R est différent de zéro, alors la suite ne peut pas être arithmétique. Nous en concluons qu'il n'existe pas de valeur possible pour U0 qui donne une suite arithmétique.

Difficile : somme avec termes arithmétiques

La méthode de la quantité conjuguée est une technique mathématique très utile pour simplifier les racines dans les problèmes. Pour montrer que la somme des racines d'une suite arithmétique de réels positifs est égale à un certain résultat, on peut utiliser cette technique et la définition de la suite arithmétique pour démontrer que le résultat est égal à la somme de racines spécifiques de la suite. En utilisant la technique de la quantité conjuguée encore une fois, on peut simplifier ces racines et trouver la solution finale. La maîtrise de cette technique peut faciliter la résolution d'autres problèmes similaire, et il est important de bien la comprendre.

Deux suites entremêlées

Ce cours aborde le sujet des suites définies de manière mélangée. Il présente deux suites, UN et VN, qui sont définies en fonction l'une de l'autre. L'objectif est de trouver des relations entre ces suites afin de résoudre le problème. Le professeur utilise des techniques mathématiques telles que les identités remarquables pour simplifier les expressions. Il introduit également le concept de suite constante et explique comment utiliser des relations linéaires pour résoudre le problème. L'idée principale est de développer des intuitions mathématiques et des méthodes de résolution pour réussir en mathématiques. La transcription de la vidéo est adaptée pour optimiser le référencement SEO.

Suite géométrique inconnue

Dans cette vidéo, l'objectif est de déterminer les suites géométriques qui vérifient la relation suivante : UN+2 - UN+1 = (U0 * Q^N+1) - (U0 * Q^N). On utilise la notation UN qui est égal à U0 * Q^N pour écrire une suite géométrique en général. Après avoir simplifié l'équation, on trouve que les suites géométriques de raison 1 ou de raison 1/2 vérifient cette relation. Si Q appartient à R étoile et U0 appartient à R étoile, alors on peut trouver des solutions non triviales.

Convergence d'une somme de termes

Ce cours présente un exercice mathématique qui consiste à étudier la convergence d'une suite. On observe une série de termes allant de 1 à n, dans laquelle seul le numérateur varie. L'objectif est de mettre tous les termes au même dénominateur afin de faciliter l'étude de la convergence. En effectuant des simplifications successives, on obtient finalement que la suite converge vers 1/2. L'auteur insiste sur l'importance de ne pas se décourager devant un exercice complexe et encourage les étudiants à avancer étape par étape en explorant les chemins les plus simples. Il souligne également qu'il est normal de ne pas trouver immédiatement la solution et que la confiance en soi est primordiale pour résoudre les exercices. L'objectif est d'utiliser les connaissances acquises et de suivre les étapes pour arriver à une conclusion.

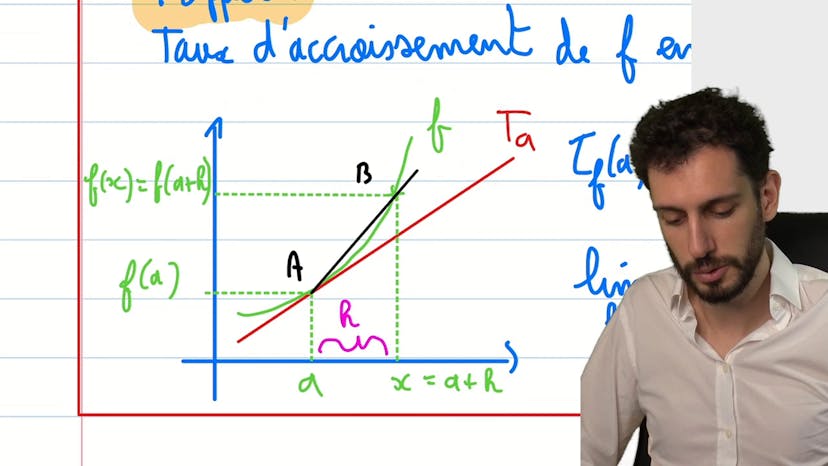
Dérivation : rappel de concept

Voici un résumé du cours :La dérivation permet de savoir si une fonction est en train de croître ou de décroître en se rapportant à des droites, appelées tangentes, plus faciles à étudier. Pour trouver la valeur de la pente de la tangente, on utilise la méthode de la corde AB, en prenant la limite du taux d'accroissement de la fonction F au point A, quand la distance H devient nulle. Cette limite est appelée nombre dérivé, noté f' de A, qui représente la pente de la tangente au point A. Le nombre dérivé est la manière courte de désigner la pente de la tangente.

Calcul de nombre dérivé

Dans ce cours, nous montrons qu'une fonction est dérivable en un point en appliquant la définition fondamentale qui stipule qu'une fonction est dérivable en un point si son taux d'accroissement admet une limite finie unique. Nous prenons pour la fonction h l'expression du taux d'accroissement au point 2 et simplifions l'expression pour obtenir une unique fraction au final. Ensuite, nous prenons la limite de cette expression simplifiée lorsque x tend vers 2 pour trouver une limite finie unique de la fonction h en ce point. Nous concluons que la fonction h est dérivable en 2 et que la limite du taux d'accroissement est égale à –7. Nous conseillons de simplifier l'expression du taux d'accroissement avant de prendre la limite afin de limiter les erreurs éventuelles.

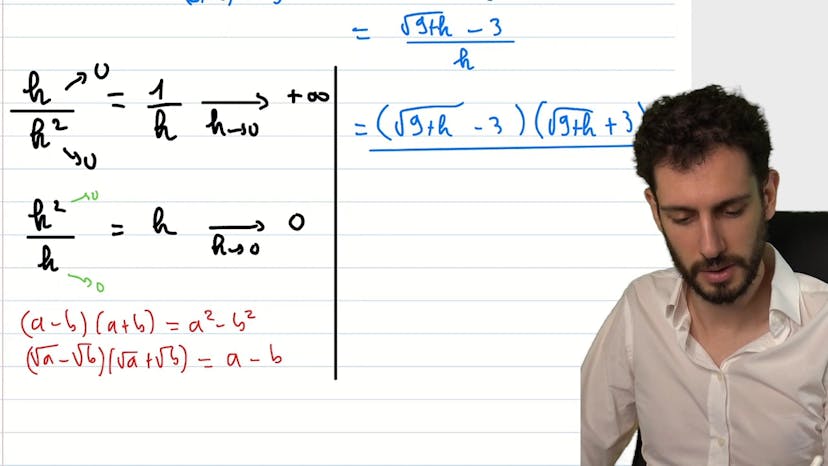
Nombre dérivé : la quantité conjuguée

Dans cet exercice de mathématiques, nous apprenons comment calculer la limite d'un taux d'accroissement pour montrer qu'une fonction est dérivable en un point. Pour cela, nous utilisons la méthode de quantité conjuguée qui est une transformation classique lorsque nous avons une expression de racine. Nous examinons également le problème de la division de 0 par 0, où il n'y a pas de règle spécifique à suivre. Nous cherchons ensuite une identité remarquable qui nous permet de simplifier le problème et de trouver la limite du taux d'accroissement. Cette méthode de quantité conjuguée est importante et peut être utilisée dans de nombreux autres exercices. À la fin, nous trouvons que la limite est égale à un sixième.

Rappel : être dérivable en un point

La vidéo explique ce qu'est être dérivable en un point. Pour être dérivable, le taux d'accroissement de la fonction en ce point doit avoir une limite finie et unique. La vidéo montre des exemples où une fonction ne respecte pas cette définition : par exemple, la fonction 1/x n'est pas définie en 0, donc pas dérivable, mais la racine de x est définie en 0 et pourtant n'est pas dérivable car elle admet une demie-tangente verticale et a une limite infinie. La valeur absolue de x est dérivable partout sauf en 0 où elle admet deux demie-tangentes de pentes opposées, ce qui ne respecte pas l'exigence d'une limite unique. Ces exemples montrent bien que la définition de la dérivabilité est importante pour comprendre et utiliser les fonctions en mathématiques.

Dérivée d'une fonction

La méthode présentée ici ne vise pas à montrer la dérivabilité d'une fonction en un point spécifique, mais plutôt à comprendre quand une fonction est dérivable en général et pour quel ensemble de points, ainsi qu'à calculer la fonction dérivée associée. Il est important de retenir que les problèmes surgissent quand le contenu de la racine ou de la valeur absolue est égal à zéro, car cela entraîne une non-dérivabilité. Pour les fonctions racine et valeur absolue, les problèmes surgissent généralement lorsque le contenu est égal à zéro. Il est nécessaire de vérifier si une fonction est définie sur un ensemble et de comprendre les points où elle n'est pas dérivable. Une formule permettant de dériver une fonction de racine est présentée et doit être mémorisée. Les précautions à prendre sont de faire attention lorsque le contenu de la racine est égal à zéro, car dans ce cas, la dérivation n'est pas possible.

Droite affine et tangente à une courbe

Cet exercice introduit le concept d'équation de la tangente pour la dérivation. On doit trouver l'équation d'une tangente qui passe par un point donné. Pour cela, on utilise des méthodes de troisième pour trouver la pente, le coefficient directeur d'une droite, etc. On détermine la pente alpha en utilisant la différence des ordonnées divisé par la différence des abscisses. Ensuite, on trouve le coefficient bêta en utilisant le point J et l'équation Y=alphaX+bêta. L'équation finale de la tangente est obtenue. Ce cours rappelle comment trouver l'équation d'une droite à partir de deux points et sert de base pour comprendre comment trouver l'équation de la tangente à un point d'une courbe, en utilisant la dérivation. L'équation complète de la tangente est présentée à la fin du cours et doit être apprise par cœur.