 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths
Nombres et calculs
Seconde

Factoriser pour résoudre
Dans cet exercice, on utilise la méthode du changement de variable pour résoudre une équation. En remplaçant X par x², l'équation x4 + x² = 6 devient X² + X - 6 = 0. Ensuite, on utilise la formule du produit de facteurs nuls pour trouver les solutions possibles : X = 2 ou X = -3. En ramenant X à x, on obtient finalement les deux solutions réelles X = racine de 2 ou X = -racine de 2.
Maths
Géométrie
Seconde

Vecteurs et alignement
Pour montrer que trois points sont alignés, on peut utiliser la méthode classique en utilisant des vecteurs. Trois points sont alignés si les vecteurs créés par ces points sont collinéaires. Deux vecteurs sont collinéaires s'il existe un coefficient de proportionnalité, k. On peut calculer les coordonnées de chaque vecteur en utilisant les formules xB-xA et yB-yA pour AB, et xC-xA et yC-yA pour AC. Ensuite, on peut observer que le vecteur AB est égal à moins 1 fois le vecteur AC, et donc AB et AC sont collinéaires. Cette propriété nous permet de conclure que les points ABC sont alignés.
Maths
Fonctions
Seconde

Tableau de signes avec du x²
Apprenez à résoudre les inéquations contenant des puissances supérieures à 1 en suivant ces étapes : mettre tous les termes d'un côté pour avoir 0 de l'autre côté, factoriser l'équation, entrer les valeurs de x pour lesquelles les facteurs s'annulent dans un tableau de signes, déterminer les signes de chaque facteur, puis identifier les valeurs de x pour lesquelles l'expression est positive. En appliquant cette méthode à l'inéquation x² + 4x ≥ -3x, nous obtenons que x appartient à l'intervalle moins l'infini moins 7, union 0 plus l'infini.
Maths
Nombres et calculs
Seconde

Système d'inégalités
Dans cet exo, on apprend à résoudre deux inéquations et à trouver une solution qui vérifie une inéquation mais pas l'autre. Pour résoudre les inéquations, on applique des opérations mathématiques et on obtient des intervalles I et J. Ensuite, on trace une droite graduée et on place les valeurs charnières des intervalles, à savoir -3/2 et 11/2. On voit que ce qui est en commun entre les intervalles I et J, c'est l'intervalle [-3/2, 11/2]. Ainsi, pour trouver une solution qui vérifie une inéquation mais pas l'autre, on prend un nombre qui est dans cet intervalle, mais qui n'est pas dans l'autre intervalle. Par exemple, A = 10 convient.
Maths
Fonctions
Seconde
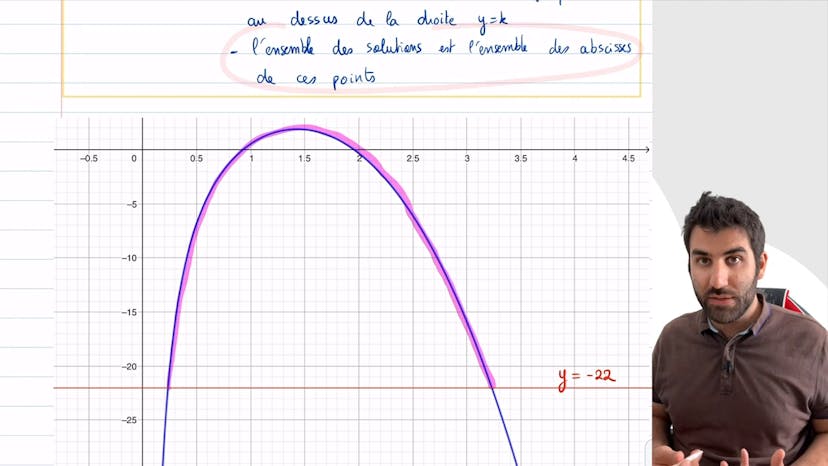
Résolution graphique : inéquation
Dans cet article, nous allons voir comment résoudre une inéquation graphiquement en trois étapes. Premièrement, nous devons tracer la courbe de la fonction f(x) supérieure à k. Deuxièmement, nous traçons la droite d'équation y=k. Enfin, nous repérons l'ensemble des points de la courbe au-dessus de la droite pour trouver l'ensemble des abscisses qui nous intéressent. Dans notre exemple, nous trace la courbe de f(x), traçons la droite y=-22, repérons l'ensemble des points au-dessus de la droite, puis nous trouvons que l'intervalle de solution graphique est entre 0,22 et 3,23.
Maths
Stats et Probas
Seconde
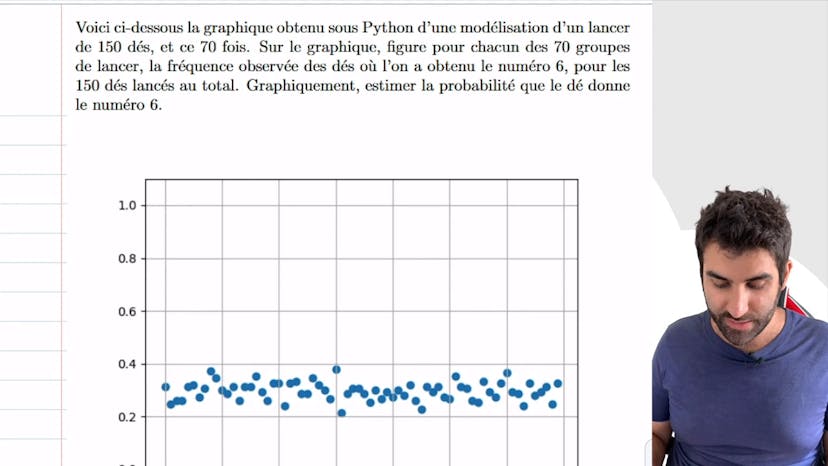
Proba à partir d'une stat ?
Dans cet exercice, on exploite le graphique d'une modélisation de lancé de dés. Nous avons lancé 150 dés 70 fois et chaque groupe de lancés a été représenté graphiquement avec la fréquence du numéro 6. La probabilité d'obtenir un 6 est estimée à environ 30%, ce qui est visible sur le graphique en observant la ligne correspondant à une fréquence de 0,3.
Maths
Géométrie
Seconde

Droite définie par deux points
Cette vidéo explique comment trouver l'équation réduite d'une droite en connaissant les coordonnées de deux points, A et B, par lesquels elle passe. Le coefficient directeur, M, est obtenu en utilisant la formule de la différence des ordonnées sur la différence des abscisses. L'ordonnée à l'origine, P, est trouvée en utilisant une équation à une inconnue avec les coordonnées d'un des points. En appliquant les formules à l'exemple fourni, la droite s'exprime finalement sous la forme Y égal 3 sur 10 X moins 31 sur 10.
Maths
Géométrie
Seconde

Application concrète des systèmes
Dans cet exercice, nous devons résoudre un problème avec deux inconnus, qui sont le prix d'un DVD et d'une BD. Nous posons X pour le prix d'un DVD et Y pour le prix d'une BD. En traduisant l'énoncé avec deux équations, nous construisons le système suivant : X + 4Y = 60,5 et 2X + 3Y = 73,5. En multipliant la première ligne par deux, nous avons 2X + 8Y = 121. Nous résolvons ensuite le système par combinaison en soustrayant la deuxième ligne de la première, ce qui nous donne 5Y = 47,5. Par conséquent, le prix d'une BD est de 9,50 €. En remplaçant Y par sa valeur dans la première équation, nous obtenons X = 22,50 €. Finalement, le prix d'un DVD est de 22,50 € et celui d'une BD est de 9,50 €.
Maths
Stats et Probas
Seconde

On joue à pile ou face !
Dans cet exercice, on réalise trois expériences aléatoires avec une pièce de monnaie et pour chaque expérience, on doit donner la loi de probabilité, c'est-à-dire la probabilité de chaque issue possible. Pour la première expérience, on fait un seul lancé et on note si c'est face ou pile, chaque option ayant une probabilité de 0,5. Pour la deuxième, on effectue deux lancés et on note l'ordre d'apparition des faces. Il y a quatre issues possibles avec une probabilité de 0,25 chacune. Pour la troisième expérience, on effectue deux lancés et on ne note pas l'ordre d'apparition des faces. Il y a trois options possibles avec une probabilité de 0,25 pour deux piles, 0,5 pour un pile et un face, et 0,25 pour deux faces.
Maths
Géométrie
Seconde

Définir une médiatrice
Dans cette leçon, on apprend à déterminer si un point se trouve sur une médiatrice. Une médiatrice est un ensemble de points se trouvant à égale distance des extrémités d'un segment. Pour vérifier si un point B appartient à la médiatrice de AC, on calcule la distance AB et la distance AC. Si les deux distances sont égales, alors le point est sur la médiatrice. Dans cet exercice, on trouve que la distance AB et la distance AC ne sont pas égales, donc le point B n'est pas sur la médiatrice du segment AC.
Maths
Stats et Probas
Seconde
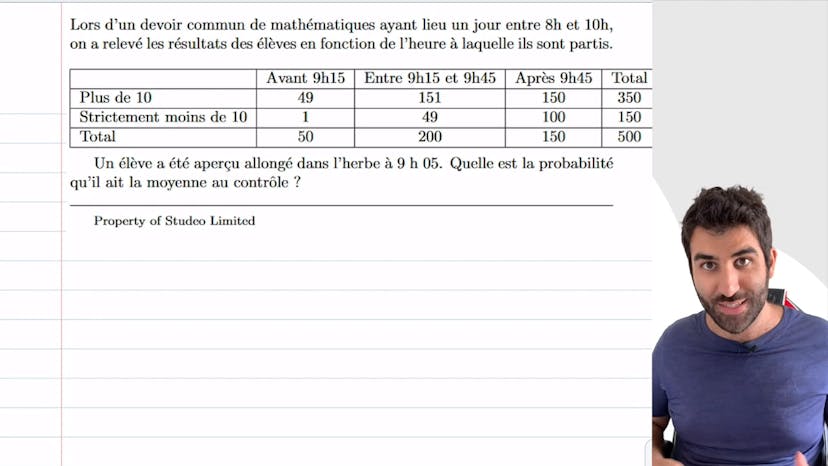
Lire un tableau de données
Dans cet exercice, nous apprenons comment utiliser un tableau de données pour déterminer la probabilité d'un événement. En l'occurrence, le contexte ici est un devoir et les notes obtenues par les élèves selon l'heure à laquelle ils ont quitté le contrôle. La question posée est la suivante : quelle est la probabilité qu'un élève allongé dans l'herbe à 9h05 ait la moyenne ? En analysant la colonne correspondante, nous en déduisons que la probabilité est de 49 sur 50 car l'élève est parti avant 9h15 et a donc plus de 10.
Maths
Fonctions
Seconde
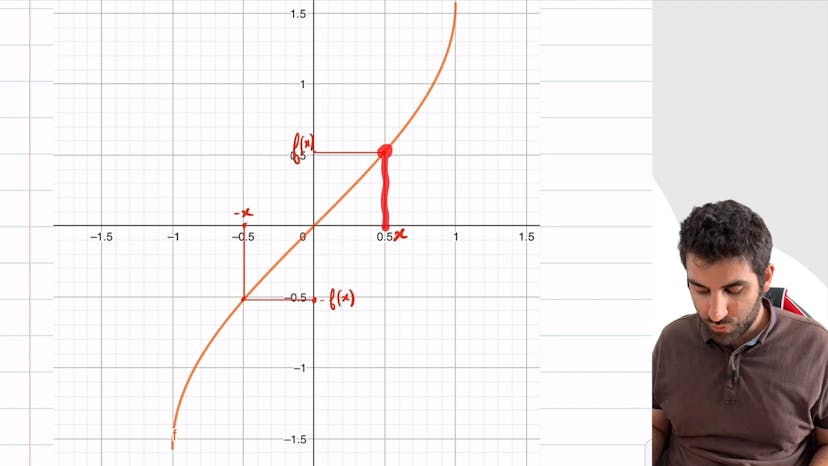
Parité d'une fonction
Cet exercice porte sur la détermination graphique de la parité d'une fonction, que ce soit paire ou impaire. Pour qu'une fonction soit paire, son ensemble de définition doit être centré en 0, et f de moins x doit être égal à f de x. En revanche, pour qu'une fonction soit impaire, son ensemble de définition doit être également centré en 0, mais cette fois-ci, f de moins x est égal à moins f de x. Pour le déterminer graphiquement, on peut prendre deux antécédents, les tracer sur le graphique, retrouver leur image, et observer si f de moins x est égal à f de x ou à moins f de x. Dans l'exemple donné, la fonction arcthynus est impaire.


