Cours d'apprentissage en ligne

Coordonnées d'un vecteur

Dans cet exercice, on cherche les coordonnées du point C pour que l'égalité entre les vecteurs AC et -2AB soit vérifiée. Pour cela, on utilise la formule des coordonnées d'un vecteur et la règle de calcul d'une multiplication entre un nombre et un vecteur. On calcule d'abord les coordonnées du vecteur AB, puis on multiplie chaque coordonnée par "-2" pour obtenir les coordonnées du vecteur -2AB. Ensuite, on calcule les coordonnées du vecteur AC en utilisant les coordonnées inconnues du point C. Enfin, pour que l'égalité soit vraie, on crée deux équations en égalant les coordonnées de chaque vecteur et on résout pour les coordonnées de C, qui sont finalement trouvées être 11 et -16.

Fonctions

Tableau de variations 1 : inéquation

L'exercice explique comment résoudre une inéquation f2x > k en utilisant un tableau de variation. Les valeurs de f2x qui sont plus grandes que k sont repérées et la solution de l'inéquation est l'ensemble des points d'abscisse correspondant à ces valeurs. Le tableau est complété avec les informations supplémentaires données pour aider à repérer les valeurs. La solution de l'inéquation est l'intervalle entre moins 7 et moins 1 exclus, ainsi que l'intervalle entre 9 exclus et l'infini si f de x est strictement plus grand que 2.

Nombres et calculs

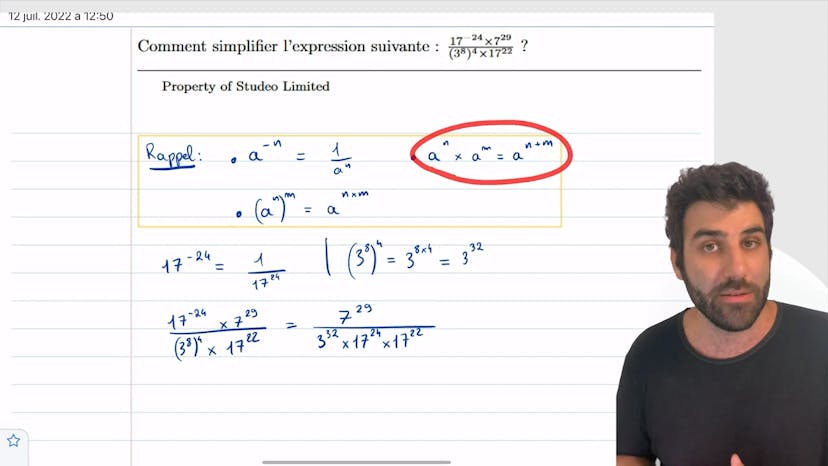
Simplifier des puissances

Dans cet exercice, on simplifie une fraction avec des puissances en utilisant 3 règles : a puissance moins n vaut 1 sur a puissance n, a puissance n fois a puissance m vaut a puissance n+m et a puissance n puissance m vaut a puissance n fois m. On applique ces règles pour réécrire 17 puissance moins 24 en 1 sur 17 puissance 24, simplifier 3 puissance 8 puissance 4 en 3 puissance 32 et regrouper les 17 sous une même puissance. On obtient ainsi la fraction simplifiée 7 puissance 29 sur 3 puissance 32 fois 17 puissance 46.

Règle du parallélogramme

Dans cet exercice, nous allons voir comment montrer qu'un quadrilatère est un parallélogramme. Nous avons besoin de deux rappels de cours. Premièrement, ABCD est un parallélogramme si les vecteurs AB et DC sont égaux ou les vecteurs AD et BC sont égaux. Nous devons faire un schéma du parallélogramme et faire attention à l'ordre des lettres. Deuxièmement, pour calculer les coordonnées d'un vecteur, nous utilisons les coordonnées de B moins les coordonnées de A. Les égalités de vecteurs sont montrées en comparant leurs coordonnées. Pour montrer que AB est égal à DC, nous calculons les coordonnées de chaque vecteur et constatons qu'elles sont les mêmes. Ainsi, ABCD est un parallélogramme.

Fonctions

Tracer une fonction symétrique

Dans cet exercice, nous apprenons à tracer la courbe symétrique par rapport à la première bissectrice d'une autre courbe. La première bissectrice est une droite qui passe par des points ayant la même abscisse que l'ordonnée. Pour tracer une courbe, nous devons faire un tableau de valeurs qui nous donne les coordonnées des points, que nous placon sur un graphique et nous les relions pour former la courbe. Pour trouver la courbe symétrique, nous devons inverser les coordonnées de la courbe initiale par rapport à l'axe Y = X. Nous faisons ensuite un tableau de valeurs de ces points qui nous donneront les nouvelles coordonnées. Nous plaçons ces points sur un graphique, en renversant l'axe des ordonnées et des abscisses et les reliant pour former notre courbe symétrique. Dans cet exercice, notre courbe symétrique est celle de la fonction racine carré.

Fonctions

Trouver un antécédent

Dans cet exercice de mathématiques, on apprend comment trouver les antécédents d'un nombre par une fonction en résolvant l'équation f(x) = k. Dans l'exemple présenté, la fonction f(x) est explicitement définie comme 2x + 7 au carré moins 4 et on cherche à trouver les antécédents de 6. Après avoir résolu l'équation, on factorise l'expression pour obtenir un produit de facteurs nul et on trouve deux solutions possibles : x = racine de 5 moins 7 et x = moins racine de 5 moins 7. Ces solutions représentent les antécédents de 6 par la fonction f.

Nombres et calculs

Comparer des expressions de x

Dans cet exo, on apprend comment comparer deux expressions numeriques A et B. La méthode consiste à trouver la différence entre A et B, puis à étudier le signe du résultat. Si A moins B est négatif, alors A est plus petit que B. Si A moins B est positif, alors A est plus grand que B. Et si A moins B est égal à 0, alors A et B sont égaux. Pour trouver le signe de A moins B, on examine l'expression MX plus P, où M est le coefficient de X et P est la constante. Si M est positif, alors l'expression affine est positive sur un intervalle. Si M est négatif, alors l'expression affine est négative sur l'intervalle. En utilisant cette méthode, on peut conclure que A est plus petit que B sur un certain intervalle, A est égal à B à un certain point et A est plus grand que B sur un autre intervalle.

Un parallélogramme

Dans cet exercice, nous devons trouver les coordonnées du point C pour que l'ABC soit un parallélogramme. On utilise la propriété que les diagonales d'un parallélogramme se coupent en leur milieu pour trouver les coordonnées. On note I le milieu de AC et DB et on utilise la formule du milieu pour trouver les coordonnées de I, qui est égal à 4 en X et 9,5 en Y. En utilisant la formule du milieu pour le segment AC, on a une équation en XC et YC. En combinant les deux égalités, on trouve que XC est égal à 10 et YC est égal à 4. Donc les coordonnées du point C sont 10,4.

Rayon d'un cercle

Ce cours explique comment déterminer si un point appartient à un cercle donné en vérifiant si la distance entre le centre du cercle et le point est égale au rayon du cercle. Cette méthode implique de calculer la distance entre les coordonnées du centre et du point en utilisant la formule de la distance entre deux points. Dans l'exemple donné pour vérifier si A appartient au cercle de centre B et de rayon 5, la distance AB a été calculée en utilisant la formule et s'est avérée être égale à 5, qui est également le rayon du cercle, ce qui prouve que A appartient bien au cercle en question.

Système d'équations : Combinaison

Dans cet exercice, on apprend à résoudre un système d'équations en utilisant la méthode de substitution et la méthode par combinaison. Nous avons un système d'équations, 2x + 5y = 8 et -6x + 3y = -5, que nous résolvons en utilisant la méthode par combinaison. Nous multiplions la première ligne par 3 pour obtenir 6x + 15y = 24 et nous la combinons avec la deuxième ligne. Nous éliminons ensuite les x en ajoutant L1 et L2 et nous trouvons la valeur de y. Nous remplaçons ensuite y dans l'une des équations pour trouver x. La solution du système est donc le couple xy qui est 13 sur 12 et 7 sur 6.

Stats et Probas

Pourcentage sur 3 ans

Dans cet exercice, nous apprenons comment faire une hausse pour rattraper une hausse avec un retard de 3 ans. Nous sommes confrontés à une situation dans laquelle les prix augmentent de 2% chaque année, mais le salaire de Nora n'a pas augmenté. Ainsi, pour déterminer l'augmentation de X%, nous devons multiplier par 1 plus X sur 100. Une augmentation de 2% correspond donc à une multiplication par 1,02 chaque année. Comme le salaire de Nora n'a pas augmenté depuis 3 ans, nous avons multiplié par 1,02 x 1,02 x 1,02, ce qui correspond à 1,0612. Donc, pour rattraper cette hausse de salaire, il faut multiplier le salaire de Nora par 1,0612, soit une augmentation de 6,12%.