Cours d'apprentissage en ligne

Bornes supérieure et inférieure

Dans cette vidéo, on cherche à trouver les bornes supérieures et inférieures d'un ensemble. L'exemple utilisé est l'ensemble A, qui est composé de 1/n plus ou moins 1, avec n qui décrit n étoiles. Pour trouver les bornes, on doit comprendre comment les éléments de A évoluent. On peut ainsi remarquer que le terme en 1/n décroît vers 0, et que le terme en moins 1/n oscille entre -1 et 1. En examinant les premiers termes, on peut déduire que le plus grand élément de A est 3,5, et que le plus petit est -1. En utilisant des théorèmes d'encadrement, on peut démontrer que la borne inférieure de A est -1, et que la borne supérieure est 3,5. Cette méthode ne nécessite pas toujours de revenir à la définition de la borne supérieure et inférieure avec ε, mais peut être utilisée avec des suites et des théorèmes d'encadrement.

Suites adjacentes

Aucun résumé n'est disponible pour cette vidéo

Irrationnalité de e

Dans ce cours, l'objectif est de montrer que la constante mathématique E est irrationnelle. Cette méthode est plus complexe que celle utilisée pour démontrer l'irrationalité de log de 2 et de la racine de 2, mais elle est guidée. L'énoncé invite à montrer une relation sur E et à encadrer la différence entre cette relation et E. Pour la première question, on utilise une récurrence. Pour encadrer la différence, on utilise l'intégrale de la première question et on essaie de la majorer et de la minorer. Enfin, pour montrer que E est irrationnelle, on suppose qu'elle est rationnelle puis on cherche une absurdité. Il suffit alors de prendre un n bien choisi pour montrer que l'hypothèse est fausse et donc que E est irrationnelle. Cela prouve l'intérêt de cette méthode élégante pour démontrer l'irrationalité de E.

Diamètre d'un ensemble

Dans cet exercice, on veut montrer que le sup de l'ensemble des valeurs absolues de x-y avec x et y qui parcourent A tout entier, c'est égal à sup de A-imp. Pour cela, on utilise la définition de la borne sup avec des petits epsilon. On démontre d'abord que sup de A-imp de A est un majorant de l'ensemble recherché, puis que c'est le plus petit des majorants en utilisant le fait que M et m sont les bornes sup et inf de A. En posant epsilon supérieur à 0 et en utilisant les bornes sup et inf, on montre que sup de l'ensemble B, les valeurs absolues de y-x, est égal à sup de A moins inf de A.

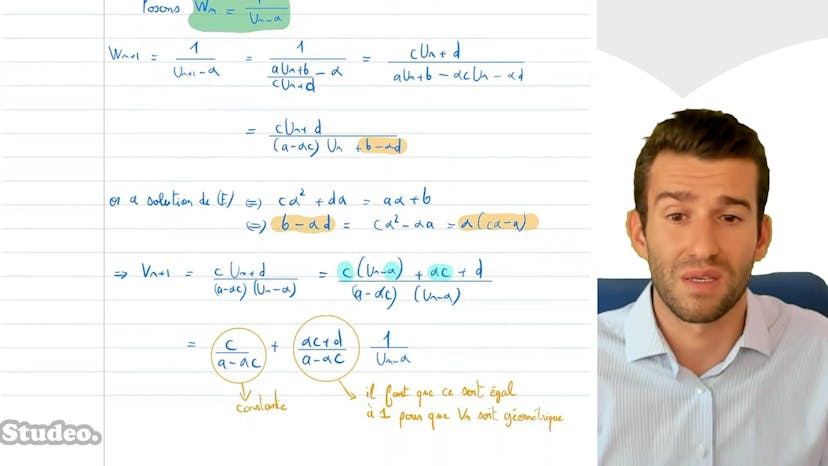
Suite homographique

Une suite homographique est une suite qui vérifie une relation de récurrence de la forme un+1=(aun+b)/(cun+d) définie par récurrence. Si la suite a deux solutions, on pose une suite auxiliaire qui est géométrique. Si elle a une seule solution, on pose une suite auxiliaire qui est arithmétique. On peut trouver l'expression de ces suites auxiliaires et remonter à l'expression de la suite homographique. On illustre cela avec deux exemples de suites homographiques.

Encadrement

Dans ce cours, nous allons découvrir une astuce d'encadrement en mathématiques. Cette astuce est facile et rapide, mais il faut la maîtriser pour pouvoir l'utiliser lors d'exercices. Nous avons deux suites de règles entre 0 et 1, et nous voulons prouver que les deux convergent vers 1. Pour ce faire, nous utilisons la méthode d'encadrement en exprimant la suite un entre 1 et vn, où vn tend vers 1, et en appliquant le théorème d'encadrement pour montrer que la suite un converge vers 1. La même méthode s'applique à la suite vn. Il est important de maîtriser cette astuce car elle peut être utile dans de nombreux exercices.

Suites adjacentes

Ce cours traite des suites adjacentes et leur étude de la variation. Les suites sont couplées et ont une relation de récurrence impliquant UN plus UN, UN-VN et VN plus UN. Le but est de déterminer une combinaison linéaire pour simplifier le problème. En calculant UN plus UN moins UN, on trouve que VN moins UN est une suite géométrique de raison un tiers avec un signe constant. Les sens de variation des deux suites UN et VN sont opposés, donc elles sont monotones, l'une croissante et l'autre décroissante. Les suites ont une différence qui tend vers zéro, donc elles convergent vers une même limite commune L. En trouvant la combinaison linéaire et en passant à la limite, on obtient une équation pour déterminer L. Le cours suggère de trouver soi-même les combinaisons linéaires, ce qui est un peu plus compliqué qu'en terminale.

Nombre d'or

Le nombre d'or est une valeur mathématique importante. Dans cette vidéo, nous abordons une suite particulière définie avec des radicaux, et nous cherchons à déterminer son comportement. Pour cela, nous montrons que la solution positive de l'équation x²-x-1, appelée phi, est comprise entre 1 et 2. Ensuite, nous exprimons la suite en fonction de phi. Nous montrons que la suite est croissante et qu'elle converge vers phi. Nous démontrons également que la convergence est très rapide, en utilisant une inégalité géométrique. Cette méthode permet de déterminer la vitesse de convergence vers une limite en mathématiques.

Bolzano Weierstrass

Bonjour à tous, dans ce cours nous allons étudier le théorème de Bolzano-Weierstrass. Pour bien comprendre cette mécanique, il faut être rigoureux et bien poser les sous-suites extraites. En suivant ces étapes avec précision, nous pourrons résoudre le problème de manière calme et rigoureuse. Nous définissons une suite complexe avec une relation de récurrence de la forme un+2 = un+1 + un/2πi. Nous posons une suite auxiliaire Mn, qui correspond au maximum des valeurs absolues des deux termes consécutifs un et un+1. Notre objectif est de montrer que Mn+1 est inférieur à (1+1/(2πi))^n+1. Nous utilisons alors la propriété que le maximum est forcément plus grand que les deux valeurs. Ainsi, un est inférieur à Mn et un+1 est également inférieur à Mn, ce qui démontre cette inégalité. Ensuite, nous tentons de majorer Mn. Pour cela, nous utilisons l'inégalité ln(un+x) < x, que nous transformons ensuite en une inégalité sur l'exponentielle. Ou alors, nous utilisons l'inégalité un+x < 2x, qui revient au même. Dans tous les cas, nous utilisons une inégalité connue sur l'exponentielle ou le logarithme. Ensuite, nous utilisons le théorème de Bolzano-Weierstrass pour la question 3. Nous savons qu'il existe une fonction Phi telle que un de Phi(n) converge. Cette suite convergente est notre suite fameuse. Nous voulons ensuite déterminer un réel A super A0 pour lequel un de Phi(n) - un est inférieur à A^n. Pour cela, nous décomposons simplement un de Phi(n) - un en plusieurs termes et démontrons que cela fonctionne. Enfin, pour la dernière question, nous devons revenir à la définition de la limite pour trouver une réponse claire. Nous montrons que Mn est bornée en utilisant le théorème de Bolzano-Weierstrass, qui nous dit que nous pouvons extraire une suite convergente de cette suite bornée. En conclusion, nous avons utilisé différentes techniques, notamment le théorème de Bolzano-Weierstrass, pour résoudre ce problème de manière rigoureuse et précise.

Suite implicite

Ce cours traite des suites implicites, qui sont plus compliquées que les suites explicites car elles ne possèdent pas d'expression explicite en fonction de n. Cependant, elles sont vérifiées par une équation. Le cours montre comment étudier ces suites en examinant leur sens de croissance et leur convergence. L'exemple présenté est une suite de polynômes qui possède une seule racine dans R+, notée Un. La suite Un est déduite comme décroissante et convergente, avec une limite de 1,5. La clé pour travailler sur les suites implicites est de partir de l'équation qu'elles vérifient plutôt que de leur valeur explicite.

Suite implicite

Aucun résumé n'est disponible pour cette vidéo