 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths Spé
Analyse
Terminale
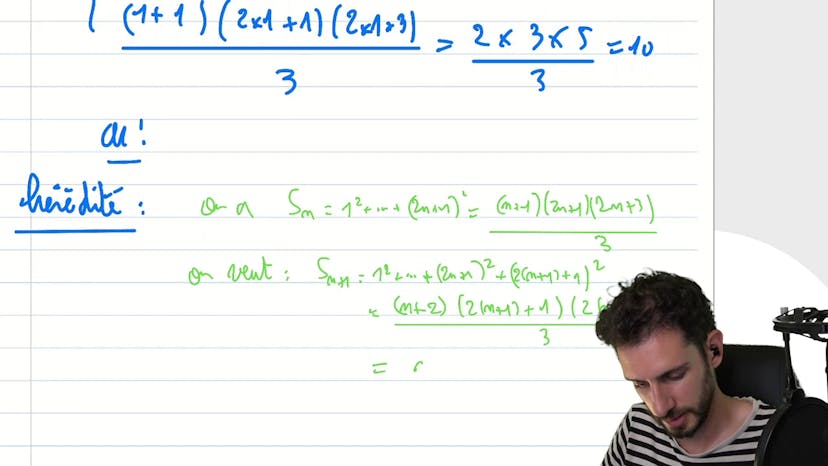
Avec une Somme
Ce cours traite d'une démonstration mathématique par récurrence. L'exemple donné est la démonstration que la somme des carrés des nombres impairs jusqu'à un certain nombre N est égale à (2N + 3)²/3. Le cours explique la méthode de rédaction pour une démonstration par récurrence, en soulignant l'importance de suivre les instructions du professeur et d'écrire de manière claire et précise. L'exemple est décomposé en différentes étapes, avec des explications détaillées sur chaque étape. L'auteur souligne également l'importance d'écrire la réponse souhaitée dès le début de la démonstration, afin de faciliter le raisonnement et de ne pas se perdre. Finalement, le cours conclut en montrant que la démonstration a été réussie grâce à la méthode de récurrence.
Maths Spé
Analyse
Terminale

Majoration 'simple'
Le cours consiste en une démonstration mathématique par récurrence, mais il est difficile de le résumer en termes SEO-friendly car il contient principalement des fragments de phrases, des notations mathématiques et des explications de raisonnements logiques. Cependant, l'objectif de la démonstration est de prouver une propriété en utilisant deux étapes : l'initialisation et l'hérédité. Finalement, la conclusion est que la propriété est démontrée.
Maths Spé
Analyse
Terminale

Trop de puissance !
Ce cours traite d'une suite définie par une relation de récurrence. Il explique comment calculer les termes de la suite en fonction du terme initial et de l'indice. Le processus se divise en deux étapes : l'intuition du résultat et la démonstration par récurrence. On montre que la suite peut être représentée par la formule u_n = u_0^(2^n). La démonstration de cette formule est simple et se fait facilement par récurrence. En conclusion, il est important de se familiariser avec les techniques de résolution d'exercices difficiles, car cela sera utile tant au lycée qu'à l'université.
Maths Spé
Analyse
Terminale

Majoration plus costaude
Ce cours est une transcription d'une vidéo qui aborde un exercice intermédiaire en mathématiques. L'objectif est de démontrer une égalité en utilisant la récurrence. Le professeur commence par expliciter les différentes étapes de la récurrence et calcule les termes de chaque côté de l'équation. Il souligne l'importance de faire ces calculs même si certains termes sont triviaux, car cela permet de vérifier que l'égalité est vérifiée à chaque étape.
Ensuite, le professeur aborde l'étape de l'hérédité où il introduit une formule clé, la formule du sinus d'une somme. Il explique qu'il est essentiel de connaître cette formule pour résoudre l'exercice. Il introduit également la notion d'inégalité et reconnaît que cela peut être un concept difficile à appréhender pour certains élèves. Il encourage cependant les élèves à s'y intéresser car cela peut être utile dans la résolution d'exercices.
Le professeur propose ensuite une démarche pour résoudre l'exercice, en cherchant à faire apparaître le terme sin(nx). Il utilise la formule du sinus d'une somme pour développer sin(nx + x). Il remarque alors qu'il a un terme en nx + quelque chose et fait appel à la formule sin(a + b) pour simplifier ce terme. Il applique ensuite l'inégalité triangulaire pour majorer les termes et cherche à isoler le terme sin(nx) en dehors des valeurs absolues.
Le professeur conclut en montrant que l'égalité est démontrée par récurrence en utilisant les bonnes formules et en faisant des majorations. Il souligne l'importance de connaître les formules mathématiques mais aussi de savoir les utiliser correctement et de pouvoir poser les bonnes questions pour résoudre un problème.
Maths Spé
Analyse
Terminale

Déf formelle
Ce cours traite de la continuité des fonctions en mathématiques. La définition informelle de la continuité est que si une fonction peut être tracée sans lever le stylo, elle est continue. La définition formelle de la continuité en un point est que la limite finie de f (x) lorsque x s'approche de a est égale à f (a). La limite finie en un point est atteinte lorsque l'on peut trouver un couloir de taille arbitraire, dans lequel toutes les valeurs de la fonction pour les x dans ce couloir sont comprises dans une zone définie. Si cela est possible pour n'importe quelle taille de couloir, la limite finie est atteinte, et si la limite finie est f (a), la fonction est dite continue en ce point.
Maths Spé
Analyse
Terminale

Discontinuités : exemples
La continuité d'une fonction est définie par une limite finie en un point qui est égale à la valeur de la fonction en ce point. Si pour un couloir fixé, toutes les valeurs de la fonction dans un couloir vertical atteignent le couloir orange, alors la fonction est continue. La discontinuité peut survenir pour diverses raisons, comme la non-existence d'un point ou une saute soudaine dans la fonction. Si la discontinuité est basée sur l'impossibilité de définition, comme dans le cas de 1/x en 0, alors la fonction n'est même pas continue. Si la discontinuité est rattrapable, comme dans le cas du sinus sur x avec un point ajouté en 0, alors la fonction est considérée comme prolongeable par continuité.
Maths Spé
Analyse
Terminale

Fonctions usuelles
Ce cours explique les fonctions continues, qui sont celles qui ne présentent pas de saut ou de trou dans leur graphique. Les fonctions les plus courantes sont continues, comme les fonctions racine carrée, exponentielle, sinus et cosinus. Les fonctions construites à partir de combinaisons ou de compositions de fonctions continues sont également continues. Les fonctions non continues sont souvent créées par morceaux et par branches. Il y a différents types de discontinuité, comme la discontinuité par définition (exemple : 1/x n'est pas défini en 0), les sauts de discontinuité, les discontinuités prolongeables et les discontinuités en un point mal placé non-prolongeables. Enfin, l'ensemble de définition (l'ensemble sur lequel une fonction est définie), l'ensemble de continuité (où une fonction est continue) et l'ensemble de dérivabilité (où une fonction est dérivable) ne sont pas toujours égaux pour une fonction donnée. Par exemple, la fonction valeur absolue de x est continue sur R, mais n'est pas dérivable sur R.
Maths Spé
Analyse
Terminale
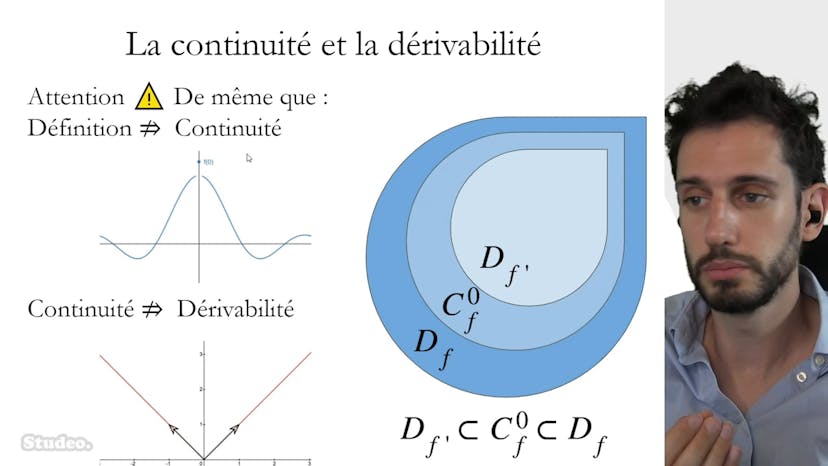
Continuité vs dérivabilité
Ce cours explique le lien entre dérivabilité et continuité. Si une fonction est dérivable en un point, alors elle est continue en ce point, mais le contraire n'est pas vrai. La démonstration utilise la limite de la fonction et le taux d'accroissement en ce point pour arriver à la définition de la continuité. L'ensemble des réels où la fonction est définie est plus grand que l'ensemble où elle est continue et l'ensemble où elle est dérivable est contenu dans l'ensemble où elle est continue. Deux exemples de fonctions continues mais non dérivables sont la racine carrée en zéro et la valeur absolue.
Maths Spé
Analyse
Terminale

Continuité et suites : Théorème du point fixe
Le théorème du point fixe est un résultat important en mathématiques qui s'applique à l'étude des suites. Il dit que si une fonction continue f sur un intervalle i a un point fixe l tel que f(l)=l, alors toute suite définie récursivement par un+1=f(un) converge vers ce point fixe l. Cependant, il est important de noter que la continuité de la fonction est nécessaire pour que ce théorème fonctionne. Enfin, il existe différents types de convergence possibles pour les suites définies de manière récurrente, en fonction de la courbure de la fonction.
Maths Spé
Analyse
Terminale
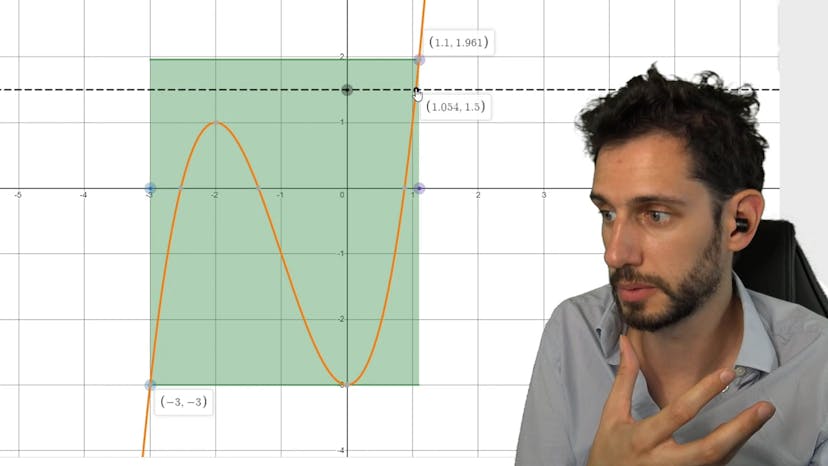
TVI : LE théorème
Le théorème des valeurs intermédiaires est capital en continuité et est utile pour les études de fonctions et la résolution d'équations. En bref, si f est une fonction continue sur un intervalle a, b pour tout réel k compris entre f2a et f2b, l'équation f2x égale k admet au moins une solution c dans l'intervalle a, b. Lorsque la fonction trace des zigouigouis, les valeurs de k peuvent croiser la fonction plusieurs fois, mais lorsque la fonction est strictement croissante ou décroissante, elle ne croisera la valeur de k qu'une seule fois. Il est important de citer le théorème des valeurs intermédiaires pour justifier son utilisation et pour identifier les solutions pour chaque intervalle où la fonction est bijective ou strictement croissante/décroissante. Le théorème de la bijection est un autre nom pour le théorème des valeurs intermédiaires, mais uniquement pour les cas de strictes croissances ou décroissances.
Maths Spé
Analyse
Terminale

Composition : Déf
La composition de deux fonctions consiste à appliquer une première fonction à une variable, puis appliquer une deuxième fonction au résultat obtenu. Il est possible de décomposer une fonction en plusieurs étapes. Par exemple, pour la fonction racine de x² + 7, il est possible de la décomposer en trois étapes : d'abord on passe de x à x², puis de x² à x² + 7, puis on prend la racine de x² + 7. La composition de deux fonctions est associative, mais pas commutative. Il est important de faire attention aux ensembles de définition des fonctions utilisées lors de la composition.
Maths Spé
Analyse
Terminale
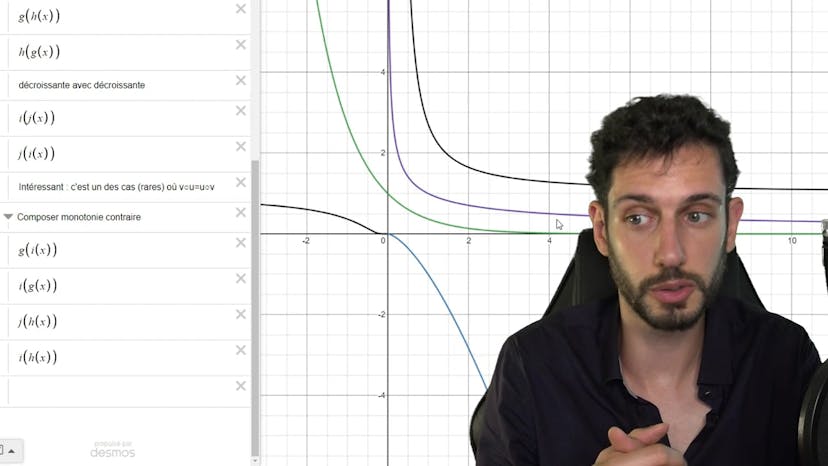
Dériver une composée
Dans cette vidéo, on apprend à dériver une fonction composée. Tout d'abord, on rappelle ce qu'est la composition et les contraintes sur les ensembles d'arrivée, le départ et les fonctions qu'on compose. Ensuite, on utilise des exemples simples pour illustrer la dérivation de fonctions composées. On remarque que dans toutes les formules, il y a un facteur u prime à ne pas oublier. On donne ensuite la formule générale de dérivation pour les fonctions composées. On explique également qu'une fonction composée de deux fonctions de même monotonie est croissante, tandis qu'une fonction composée de deux fonctions de monotonies opposées est décroissante. Des exemples sont donnés pour illustrer ces concepts.


