Cours d'apprentissage en ligne

Application avec contexte

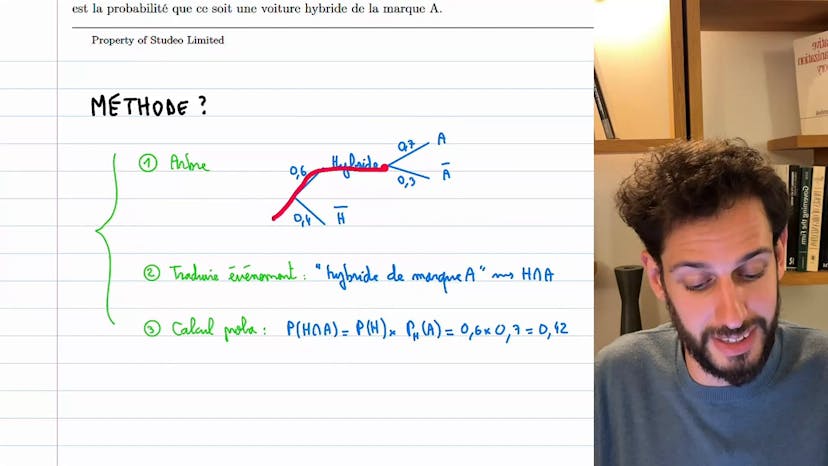
Dans cette transcription vidéo, il est question d'une application utilisant les probabilités conditionnelles. On considère une usine où 60% des voitures fabriquées sont des voitures hybrides, dont 70% sont de marque A. L'objectif est de déterminer la probabilité qu'une voiture choisie aléatoirement à la sortie de l'usine soit une voiture hybride de marque A. Le conférencier utilise le concept d'arbre pour représenter les différentes possibilités. Il note que la première partition de l'univers est d'avoir une voiture hybride (60%) ou de ne pas en avoir (40%). Dans le sous-univers des voitures hybrides, il y a celles de marque A ainsi que d'autres marques non spécifiées. En utilisant la formule des probabilités conditionnelles, le conférencier calcule la probabilité recherchée. Il indique que la probabilité d'avoir une voiture hybride de marque A (noté H inter A) peut être calculée en multipliant la probabilité d'avoir une voiture hybride (60%) par la probabilité d'avoir une voiture de marque A sachant qu'elle est hybride (70%, conditionnelle à H). Ainsi, la probabilité recherchée est de 0,6 * 0,7, soit 42%. Le conférencier souligne que ce raisonnement peut sembler intuitif, mais qu'il est important de bien comprendre et appliquer les notions du cours. Il précise qu'il existe d'autres méthodes pour résoudre ce type d'exercice et invite les participants à poser des questions s'ils en ont besoin. Dans l'ensemble, ce cours explique de manière simple et détaillée comment calculer la probabilité qu'une voiture choisie aléatoirement à la sortie d'une usine soit une voiture hybride de marque A, en utilisant les probabilités conditionnelles et en visualisant le problème à l'aide d'un arbre.

Arbre et urne sans remise

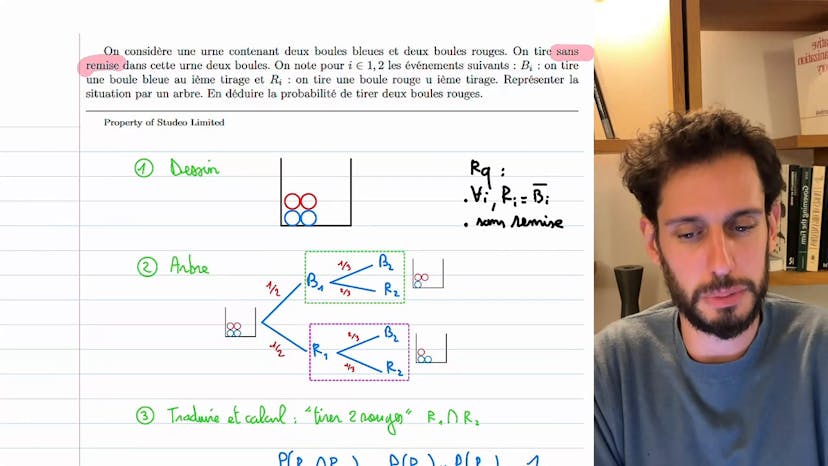
Ce cours porte sur les probabilités de tirage sans remise. L'enseignant explique qu'il est important de repérer dès le départ si on est dans le monde de sans remise ou de remise, car cela va vraiment changer la situation. Il présente un exemple avec une urne contenant des boules bleues et rouges, et explique que tirer sans remise signifie que chaque fois qu'on tire une boule, on ne la remet pas dans l'urne. Il présente également les notations bi (tirer une boule bleue au ième tirage) et ri (tirer une boule rouge), soulignant que ri est en fait le complémentaire de bi. Il utilise des dessins pour illustrer les différentes situations et sous-univers, et explique que les probabilités vont changer en fonction du nombre de boules restantes dans l'urne. Il explique ensuite comment calculer la probabilité d'avoir tiré deux boules rouges en utilisant la formule des probabilités conditionnelles. Il conclut en invitant les étudiants à poser des questions et en annonçant une prochaine vidéo.

Indépendance : calculatoire

Dans cet exercice, nous avons une entreprise qui a deux rendez-vous, un avec chaque fournisseur. La probabilité de signer un contrat avec le premier fournisseur est de 0,7, tandis que la probabilité de signer un contrat avec le deuxième fournisseur est de 0,4. Les deux événements sont considérés comme indépendants, ce qui signifie que nous pouvons signer avec les deux fournisseurs si nous le souhaitons. L'événement "aucun contrat" correspond au fait de ne pas signer de contrat avec les deux fournisseurs. Nous le notons S1 bar inter S2 bar, ce qui signifie que nous ne signons pas de contrat avec le premier fournisseur et le deuxième fournisseur à la fois. La probabilité de cet événement est égale à la probabilité de ne pas signer de contrat avec le premier fournisseur (1 - 0,7) multipliée par la probabilité de ne pas signer de contrat avec le deuxième fournisseur (1 - 0,4), soit 0,3 x 0,6 = 0,18. L'événement "au moins un contrat" correspond au fait de signer au moins un contrat avec l'un des deux fournisseurs. C'est le complémentaire de l'événement "aucun contrat". La probabilité de cet événement est donc égale à 1 (100%) moins la probabilité de l'événement "aucun contrat", soit 1 - 0,18 = 0,82. En conclusion, il y a 82% de chances que l'entreprise signe au moins un contrat avec l'un des deux fournisseurs.

Indépendance : définition

Le cours porte sur la notion d'indépendance entre des événements. On nous indique qu'en France, il y a 90% de droitiers et 45% de myopes. Parmi les myopes, 10% ne sont pas droitiers. On nous demande si les événements "être droitier" et "être myope" sont indépendants. Pour résoudre cet exercice, on traduit l'énoncé en probabilités. Être droitier a une probabilité de 90% pour un français, et être myope a une probabilité de 45%. Parmi les myopes, la probabilité de ne pas être droitier est de 10%. On remarque que la probabilité de ne pas être droitier chez les myopes est de 0,1. Cela implique que la probabilité d'être droitier chez les myopes est de 0,9 (complémentaire de 0,1). En utilisant ces informations, on conclut que la probabilité d'être droitier pour toute la France est de 0,9. La probabilité d'être droitier sachant que l'on est myope est également de 0,9. Cela signifie que la myopie et le fait d'être droitier ne sont pas dépendants. En résumé, les événements "être droitier" et "être myope" sont indépendants, ce qui se déduit des probabilités fournies dans l'énoncé.

Introduction à la récurrence

Le cours introduit le principe de la méthode de démonstration par récurrence en expliquant son application aux propriétés dépendant de n. L'exemple utilisé est la formule de la somme des n entiers consécutifs. La démonstration par récurrence permet de prouver une formule dont on a déjà une intuition, en montrant que si elle est vraie à un certain rang, elle est également vraie au rang suivant. Cependant, il est important d'avoir une initialisation, c'est-à-dire un rang où la propriété est déjà vraie. Le cours propose également trois points à retenir : le principe général de la récurrence, l'initialisation qui peut commencer à un rang autre que n=0, et une inégalité classique appelée l'inégalité de Bernoulli qui peut être démontrée par récurrence. En ce qui concerne les méthodes, il est recommandé d'appliquer la récurrence aux suites, de démontrer une formule générale à partir de quelques termes connus, et de pratiquer différentes stratégies pour montrer la transmission de la propriété d'un rang à l'autre.

Concept et rédaction

Dans cette première vidéo de cours sur la récurrence, l'enseignant aborde plusieurs points importants en matière de rédaction, d'initialisation et d'erreurs à éviter. La récurrence est une méthode de démonstration utilisée en mathématiques pour prouver qu'une propriété est vraie pour tous les entiers. Pour ce faire, on démontre d'abord que la propriété est vraie pour un entier donné, puis on montre que si elle est vraie pour un certain entier, elle est également vraie pour l'entier suivant. Ainsi, en combinant cette "pichenette initiale" et cette "transmission", la propriété est vraie pour tous les entiers. Il est primordial de conclure la démonstration en mentionnant que la propriété est vraie pour tout entier. Omettre cette conclusion peut entraîner une perte de points dans l'évaluation. L'enseignant souligne l'importance de cette phrase de conclusion, en indiquant que certains professeurs pourraient même attribuer une note de zéro si elle est absente. L'enseignant remarque également que dans environ 10% des exercices, la démonstration par récurrence commence par un entier différent de zéro, comme 3 ou 4. Il insiste sur le fait que le principe reste le même dans ces cas-là. Un exemple concret de démonstration par récurrence est présenté à travers une suite numérique. L'enseignant explique les différentes étapes de la démonstration, de l'initialisation à l'hérédité en passant par la conclusion. Il rappelle aux élèves de s'adapter aux exigences de leur professeur en termes de rédaction. En conclusion, cette vidéo met en évidence l'importance de la rédaction, de l'initialisation et de la conclusion dans la démonstration par récurrence. Elle rappelle aux élèves d'être attentifs aux spécificités de chaque exercice et de suivre les indications de leur professeur pour obtenir de bons résultats.

Pourquoi l'initialisation ?

Dans cette vidéo, l'importance de l'initialisation dans le domaine de la PitchNet est discutée. Bien que l'hérédité soit généralement considérée comme l'aspect le plus important, l'initialisation ne doit pas être négligée. Un exemple est donné pour illustrer cette importance. Le sujet abordé est la propriété P2N, qui affirme que 2 puissance N est divisible par 3. En réalité, 2 puissance N n'est pas divisible par 3, mais cette propriété peut être transmise. Il est démontré que si cette propriété est vraie pour un instant N, elle sera également vraie pour l'instant N+1. Cependant, il est souligné qu'il peut être difficile de trouver une initialisation pour cette propriété, ce qui justifie l'importance de l'initialisation dans la pratique. Cette vidéo bonus conclut en rappelant l'importance de faire l'initialisation correctement dans chaque situation.

Inégalité de Bernoulli : visuel

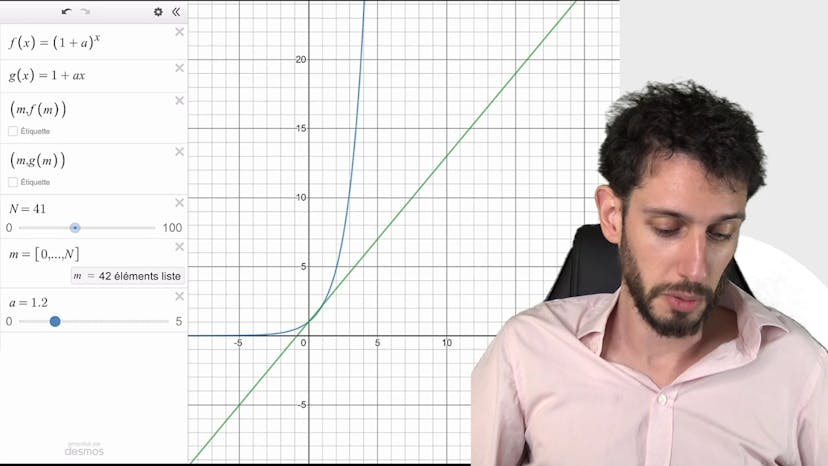
Dans cette vidéo, le professeur cherche à expliquer graphiquement l'inégalité de Bernoulli. Il explique que cette inégalité peut être démontrée grâce au principe de récurrence. Pour mieux comprendre cette formule, il propose une simulation où il compare deux fonctions: une exponentielle et une affine. Il montre que l'exponentielle monte beaucoup plus vite que la fonction affine, ce qui justifie l'inégalité de Bernoulli. Il souligne que cette inégalité est valable pour toutes les valeurs positives de A et pour toutes les valeurs de N. Il précise également que l'inégalité est vérifiée pour les entiers 0 et 1. Il encourage les spectateurs à poser des questions et à utiliser la simulation pour mieux comprendre cette inégalité.

Récurrence et croissance

La démonstration par récurrence est une technique utilisée en mathématiques pour prouver une propriété P(n) qui est vraie pour tous les entiers naturels n. Dans cette transcription d'une vidéo, nous avons un exemple de démonstration par récurrence pour prouver que la suite donnée est strictement décroissante. Pour commencer, nous définissons P(2n) comme la propriété qui est vraie au rang n dans la démonstration par récurrence. Dans ce cas, nous voulons montrer que Un+1 est plus petit que Un. Il est important de noter que la propriété de récurrence, P(2n), n'inclut pas la mention "pour tout n" car elle est seulement vraie pour un rang spécifique. Nous commençons par l'initialisation, c'est-à-dire montrer que la propriété est vraie pour le premier rang (n=0). Ensuite, nous passons à l'hérédité, où nous assumons que la propriété est vraie au rang n et essayons de montrer qu'elle est également vraie au rang n+1. Dans cet exemple, nous utilisons une relation de récurrence pour montrer l'hérédité. Nous posons la fonction f(x) = 2x - 6 et utilisons le fait que cette fonction est strictement croissante. En utilisant cette fonction, nous pouvons montrer que Un+2 est plus petit que Un+1 en composant f(Un) et f(Un+1). En conclusion, en utilisant le principe de récurrence, nous avons prouvé que pour tout entier naturel n, Un+1 est strictement inférieur à Un, ce qui signifie que la suite est strictement décroissante. Il est également souligné qu'il est important de distinguer entre le réel Un (la valeur de la suite au rang n) et l'objet suite Un (l'ensemble des valeurs de la suite). L'utilisation de parenthèses pour indiquer l'objet suite est recommandée pour éviter toute confusion.

Conjecture puis récurrence

Dans ce cours, nous avons vu comment utiliser une démonstration par récurrence pour calculer la somme des entiers de 1 à n. La formule à retenir est que la somme des entiers naturels de 1 à n est égale à n(n + 1)/2. Il est important de noter que pour utiliser cette méthode de démonstration, il faut connaître le résultat que l'on souhaite démontrer. Si vous n'avez aucune idée de la valeur de la somme des entiers naturels, vous ne pourrez pas poursuivre la démonstration. Dans cet exemple, nous allons redémontrer cette formule. Nous posons la proposition p(2n) suivante : 1 + 2 + 3 + ... + n = n(n + 1)/2. Nous supposons que p(2n) est vrai pour tout n appartenant à l'ensemble des entiers naturels. Nous commençons par l'initialisation en vérifiant que la formule est vraie pour n = 1. En effet, 1 = 1(1 + 1)/2, donc cela est vérifié. Ensuite, nous passons à l'hérédité. Nous supposons que p(2n) est vrai pour un certain n fixé. Nous souhaitons montrer que p(2n + 1) est également vrai, c'est-à-dire que 1 + 2 + ... + (n + 1) = (n + 1)(n + 2)/2. Pour cela, nous remplaçons chaque occurrence de n par (n + 1) dans la formule au rang n. Nous obtenons donc (n + 1)(n + 1 + 1)/2, ce qui se simplifie en (n + 1)(n + 2)/2. Ainsi, en appliquant cette méthode de manière itérative, nous parvenons à démontrer que pour tout entier naturel non nul n, la somme des entiers de 1 à n est égale à n(n + 1)/2.

Hérédité : comment démarrer ?

La démonstration par récurrence est un point complexe dans ce cours transcrit d'une vidéo. Il y a deux cas possibles pour montrer l'hérédité. Il est préférable de bien écrire l'hypothèse de récurrence et ce que l'on souhaite démontrer, puis de faire le lien entre les deux. Deux méthodes peuvent être utilisées : partir de l'hypothèse de récurrence et aboutir à Pn+1, ou partir de Pn+1 et se servir de P2n pour conclure. Un exemple simple est donné pour illustrer la différence entre les deux méthodes. On a une suite U définie par récurrence où U0 = 5, U1+1 = 3U1 + 6, et on veut montrer que U1 est strictement positif pour tout n. On pose P2n, qui est Un strictement supérieur à 0, et on montre que P2n est vrai pour tout n. Pour l'initialisation, U0 = 5, ce qui ne pose aucun problème. Pour l'hérédité, on peut choisir de partir de l'hypothèse de récurrence et construire Un+1 à partir de cela en multipliant par 3, ou partir de Pn+1 en utilisant l'égalité Un+1 = 3Un + 6. Les deux méthodes sont possibles, mais cela dépend de l'exercice et de la préférence de chacun. Si une méthode ne fonctionne pas, il est possible d'essayer avec l'autre. Pour plus de questions, il y a une FAQ disponible.