 All subjects
All subjects
 All subjects
All subjects
Maths
Analyse
MPSI/PCSI
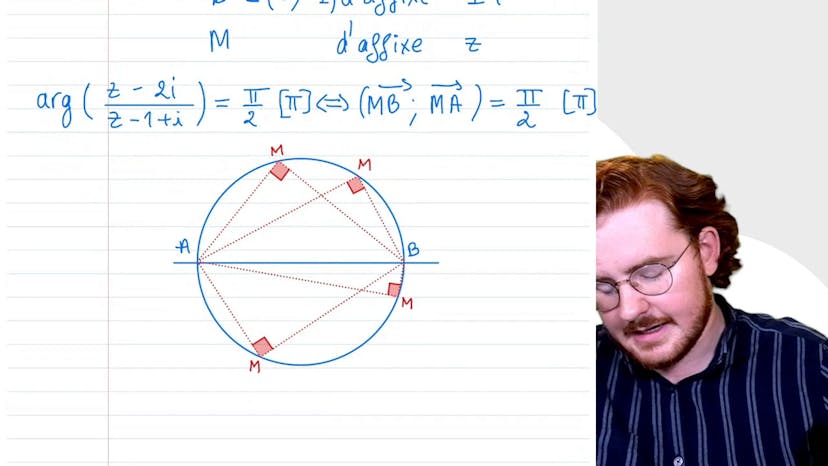
Lieu géométrique avec l’argument
Dans cette vidéo, Paul explique comment déterminer l'ensemble des points M dont la fixe Z vérifie certaines relations complexes en utilisant des objets géométriques. Pour la première question, Paul cherche les points M avec une fixe Z telle que l'argument de Z-2 est égal à pi sur 2 modulo de pi, ce qui signifie que Z est sur la demi-droite d'origine 2,0 porté par un vecteur V. Pour la deuxième question, l'argument de Z divisé par I plus I est égal à pi sur 2 modulo de 2 pi, ce qui signifie que Z est sur la demi-droite d'origine O passant par le point 1. Pour la troisième question, Paul développe une méthode pour trouver les points M tels que l'argument de Z moins 2i divisé par Z moins 1 plus i est égal à pi sur 2 modulo pi. Il utilise les points A et B ainsi que le cercle dont un rayon est AB pour déterminer l'ensemble des points recherchés.
Maths
Analyse
MPSI/PCSI

Lieu géométrique avec le module
Dans cette vidéo, Paul explique comment déterminer le lieu géométrique des points M dont la fixe Z vérifie des relations sur le module. Il commence par assimiler le plan complexe au repère OUV et pose Z égale à A plus IB pour faciliter les calculs. En calculant les carrés des modules, il simplifie les relations et détermine que l'ensemble des points M est la droite OU, soit la droite des réelles. Il répète ce processus pour la deuxième question et trouve que l'ensemble des points M est également la droite des réelles. En résumé, Paul parle de la géométrie des nombres complexes en déterminant l'ensemble des points satisfaisant des conditions sur le module, et trouve dans ce cas deux droites des réelles.
Maths
Analyse
MPSI/PCSI

Transformations du plan
Paul donne un exercice sur les transformations du plan complexe. Il demande d'identifier la nature des éléments caractéristiques des applications qui ont des formes différentes. Selon Paul, les transformations peuvent être des translations, des rotations, etc. Dans la première question, il identifie une rotation de centre haut et d'angle moins pi sur 2. Dans la deuxième question, il reconnait simplement la définition d'une translation. Dans la troisième question, il identifie une similitude de centre 1 1 avec un rapport de 2 et une argument pi sur 3. Dans la quatrième question, il découvre une similitude d'angle alpha, de ce et de rapport 1 sur cosinus alpha et de centre 1 0. Paul conclut l'exercice en disant au revoir.
Maths
Analyse
MPSI/PCSI

Lieux géométriques
Dans cette vidéo, on examine la relation entre les nombres complexes et leurs représentations géométriques. On nous demande de trouver le lieu géométrique des points vérifiant certaines conditions. Pour la première question, on doit déterminer les points alignés en traduisant une condition sur les complexes en une forme géométrique. Pour la deuxième question, on doit trouver les points où la partie réelle d'un nombre complexe est égale à zéro. Enfin, pour la troisième question, on doit identifier les sommets d'un triangle rectangle à partir de leurs affixes complexes. Les réponses sont présentées sous forme géométrique, telles que des droites, des cercles et des axes de coordonnées.
Maths
Analyse
MPSI/PCSI

Théorème de Napoléon
Dans cet exercice, nous devons démontrer que le triangle UVW est équilatéral si et seulement si U - V = -J^2(W - V), où J est une racine cubique de l'unité. Pour prouver cela, nous utilisons la géométrie des complexes.
Tout d'abord, nous rappelons que J représente une racine cubique de l'unité, et que les points U, V et W ont des affixes respectives U, V et W.
Nous remarquons que si U est l'image de W par une rotation centrée en V avec un angle de π/3, alors le triangle UVW est équilatéral direct. Cela est dû au fait que J est de module 1 et que V est le centre de cette rotation.
En partant de cette observation, nous pouvons démontrer que le triangle UVW est équilatéral direct si et seulement si l'équation U - V = -J^2(W - V) est valide.
Pour prouver cette équivalence, nous divisons l'exercice en deux sens. Tout d'abord, nous supposons que U - V = -J^2(W - V), ce qui signifie que U est l'image de W par une rotation centrée en V avec un angle de π/3. Ainsi, le triangle UVW est équilatéral direct.
Ensuite, nous supposons que le triangle UVW est équilatéral direct, ce qui implique que V - W = V - U. En utilisant les propriétés de J, nous montrons que cela est équivalent à l'équation U + JV + J^2W = 0. Par transitivité, nous obtenons l'équivalence recherchée.
Ensuite, nous abordons une question plus géométrique où nous devons construire un triangle équilatéral et trouver son centre de gravité. Nous utilisons les bissectrices pour faciliter la construction, mais cela pourrait aussi être fait avec les médianes ou les hauteurs.
Finalement, nous prouvons que le triangle formé par les centres de gravité des triangles b P,C, c Q,A et a R,B est également équilatéral direct. Pour cela, nous utilisons les expressions des affixes de ces points et montrons que leur somme est égale à zéro. De plus, nous montrons que les centres de gravité des triangles UVW et ABC coïncident.
En conclusion, nous avons démontré que le triangle UVW est équilatéral direct si et seulement si U - V = -J^2(W - V), en utilisant la géométrie des complexes.


