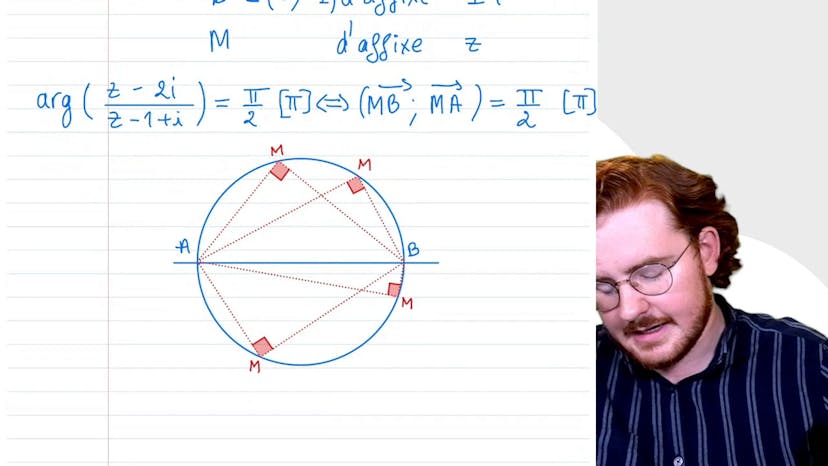
All subjects
All subjects
 All subjects
All subjects
Théorème de Napoléon
Dans cet exercice, nous devons démontrer que le triangle UVW est équilatéral si et seulement si U - V = -J^2(W - V), où J est une racine cubique de l'unité. Pour prouver cela, nous utilisons la géométrie des complexes.
Tout d'abord, nous rappelons que J représente une racine cubique de l'unité, et que les points U, V et W ont des affixes respectives U, V et W.
Nous remarquons que si U est l'image de W par une rotation centrée en V avec un angle de π/3, alors le triangle UVW est équilatéral direct. Cela est dû au fait que J est de module 1 et que V est le centre de cette rotation.
En partant de cette observation, nous pouvons démontrer que le triangle UVW est équilatéral direct si et seulement si l'équation U - V = -J^2(W - V) est valide.
Pour prouver cette équivalence, nous divisons l'exercice en deux sens. Tout d'abord, nous supposons que U - V = -J^2(W - V), ce qui signifie que U est l'image de W par une rotation centrée en V avec un angle de π/3. Ainsi, le triangle UVW est équilatéral direct.
Ensuite, nous supposons que le triangle UVW est équilatéral direct, ce qui implique que V - W = V - U. En utilisant les propriétés de J, nous montrons que cela est équivalent à l'équation U + JV + J^2W = 0. Par transitivité, nous obtenons l'équivalence recherchée.
Ensuite, nous abordons une question plus géométrique où nous devons construire un triangle équilatéral et trouver son centre de gravité. Nous utilisons les bissectrices pour faciliter la construction, mais cela pourrait aussi être fait avec les médianes ou les hauteurs.
Finalement, nous prouvons que le triangle formé par les centres de gravité des triangles b P,C, c Q,A et a R,B est également équilatéral direct. Pour cela, nous utilisons les expressions des affixes de ces points et montrons que leur somme est égale à zéro. De plus, nous montrons que les centres de gravité des triangles UVW et ABC coïncident.
En conclusion, nous avons démontré que le triangle UVW est équilatéral direct si et seulement si U - V = -J^2(W - V), en utilisant la géométrie des complexes.