 All subjects
All subjects
 All subjects
All subjects
Maths
Analyse
MPSI/PCSI
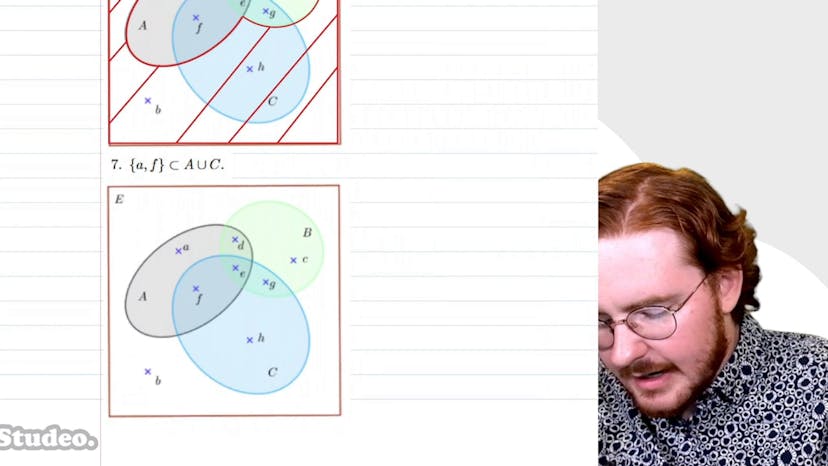
Diagramm de Venn
Dans cette vidéo, Paul utilise le diagramme de Venn pour résoudre des assertions sur les ensembles. Il montre comment déterminer si une proposition est vraie ou fausse en utilisant les croix et les patates pour représenter les ensembles. Paul illustre également les différentes opérations d'ensembles telles que l'intersection, la complémentation et l'union en utilisant le diagramme de Venn. Il encourage ses spectateurs à utiliser les diagrammes de Venn pour tester des hypothèses sur les ensembles.
Maths
Analyse
MPSI/PCSI

Intersection et Union
Dans cette vidéo, on apprend à manipuler l'union, l'intersection et l'appartenance des ensembles. On prend trois ensembles A, B et C tels que A union B est égal à B inter C. On doit montrer que A est inclus dans B et est inclus dans C. Pour montrer l'inclusion, il faut prouver que pour tout élément X de A, X est également dans B et C. On commence par montrer que A est inclus dans B en prouvant que pour tout élément X de A, X appartient à B. Sachant que A union B est égal à B inter C, on déduit que X appartient à B inter C, donc à B et C. Donc X appartient à B et A est inclus dans B. On montre ensuite que B est inclus dans C en prouvant que pour tout élément X de B, X appartient à C. Sachant que B est égal à B inter C, on déduit que X appartient à B inter C, donc à B et C. Donc X appartient à C et B est inclus dans C. Finalement, on a prouvé que A est inclus dans B qui est inclus dans C.
Maths
Analyse
MPSI/PCSI

Parties
Dans cette vidéo, Paul explique la relation entre les parties d'un ensemble en utilisant deux ensembles E et F. En analysant la question de savoir si A est une partie de E inter F et si elle est aussi une partie de E et F, il déduit que A appartient à la fois aux parties de E et de F. En comparant P de E inter F avec P E inter P de F, il démontre que P de E inter F est inclus dans P de E inter P de F. Ensuite, il essaie de prouver l'inclusion réciproque, mais il trouve un contre-exemple en utilisant les singletons. Il conclut que les choses qui sont vraies pour l'union ne le sont pas forcément pour l'intersection.
Maths
Analyse
MPSI/PCSI
Lois de Morgan
Aucun résumé n'est disponible pour cette vidéo
Maths
Analyse
MPSI/PCSI
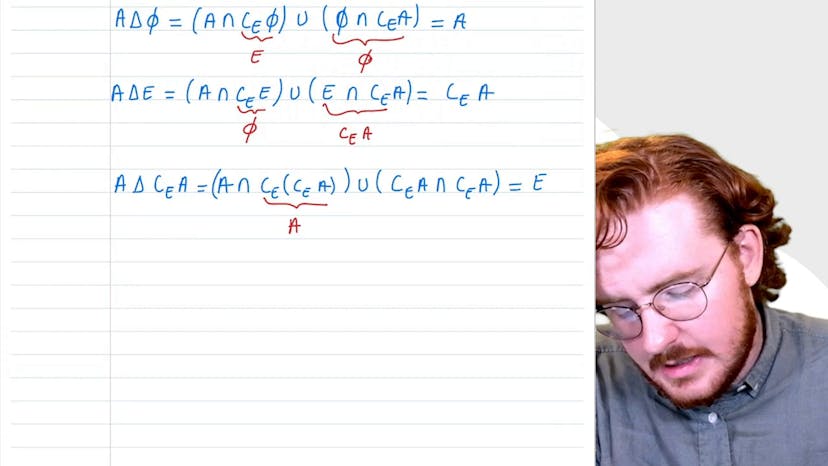
Différence symétrique
Dans cette vidéo, Paul explique la différence symétrique, définie comme delta A, delta B, qui est l'ensemble des X qui sont dans A ou B mais qui ne sont pas dans A et B. Il utilise des patates pour aider à comprendre cette définition. Il montre également une propriété de l'égalité entre deux ensembles par double inclusion. Il utilise cette propriété pour calculer quelques exemples de différences symétriques. La quatrième question consiste à démontrer la distributivité de l'intersection sur la différence symétrique. Paul procède par double inclusion pour démontrer cette relation. En fin de compte, la vidéo explique comment calculer la différence symétrique de différents ensembles.
Maths
Analyse
MPSI/PCSI
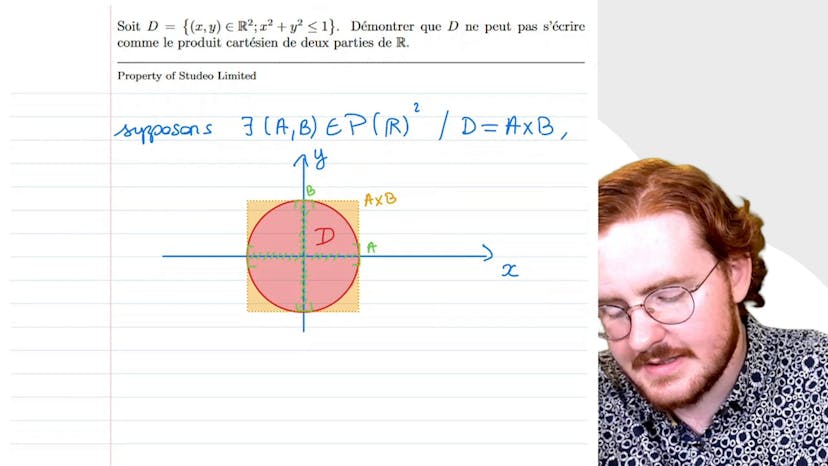
Produit cartésien
Dans cette vidéo, Paul utilise un raisonnement par l'absurde pour démontrer que l'ensemble D, qui est défini comme l'ensemble des x y appartenant au plan tel que x² plus y² est inférieur au égal à 1, ne peut pas être écrit comme le produit cartésien de deux parties de R. Il commence par supposer l'inverse de ce qu'il veut prouver, c'est-à-dire qu'il existe une écriture telle que AB appartenant aux parties de R² et que D est le produit cartésien de A et B. Ensuite, il dessine les parties A et B de R et montre que le produit cartésien A fois B va tomber en dehors du cercle dans certains endroits. Pour prouver qu'un point est à la fois dans A fois B et n'est pas dans D, il utilise les points extrêmes 0, 1 et 1, 0. Il conclut qu'il y a une contradiction et que D ne peut pas être écrit comme un produit cartésien de deux parties de R.
Mathématiques
Analyse
ECG
Diagramm de Venn
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
ECG
Intersection et Union
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
ECG
Parties
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
ECG
Lois de Morgan
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
ECG
Différence symétrique
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
ECG
Produit cartésien
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
BCPST
Diagramm de Venn
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
BCPST
Intersection et Union
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
BCPST
Parties
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
BCPST
Lois de Morgan
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
BCPST
Différence symétrique
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
BCPST
Produit cartésien
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Analyse
ECG

Diagramm de Venn
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Analyse
ECG

Intersection et Union
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Analyse
ECG

Parties
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Analyse
ECG
Lois de Morgan
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Analyse
ECG
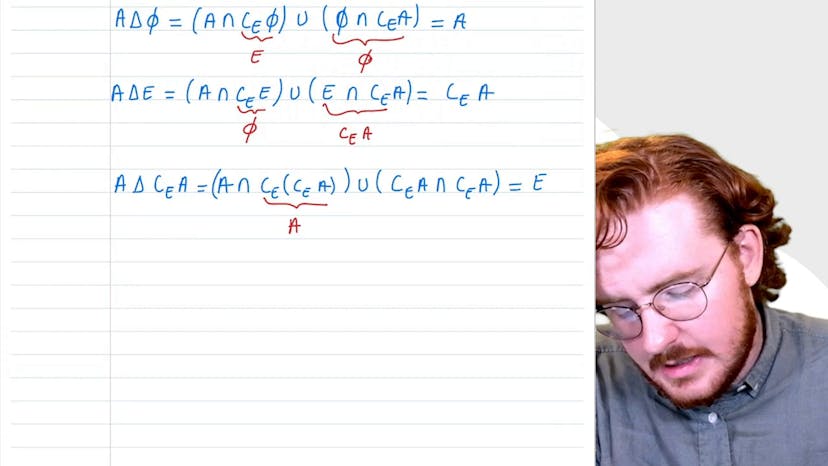
Différence symétrique
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Analyse
ECG

Produit cartésien
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Analyse
ECG

Diagramm de Venn
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Analyse
ECG

Intersection et Union
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Analyse
ECG

Parties
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Analyse
ECG
Lois de Morgan
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Analyse
ECG
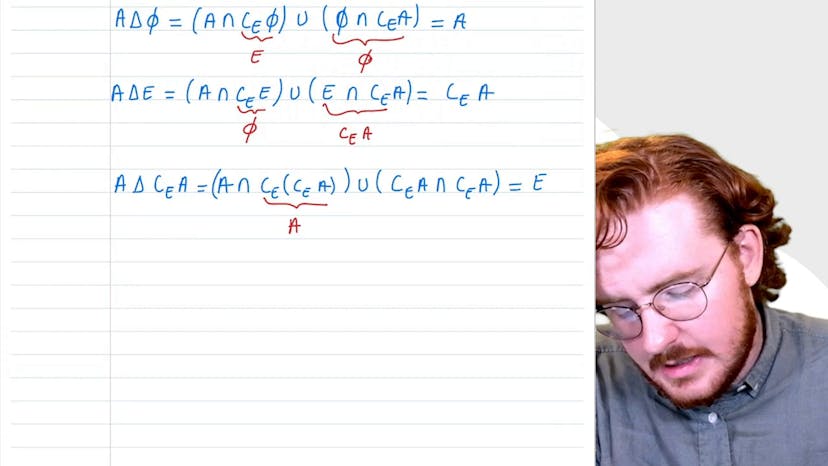
Différence symétrique
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Analyse
ECG

Produit cartésien
Aucun résumé n'est disponible pour cette vidéo


