Online Signaux physiques course by Top Instructors - Signaux physiques

Battements

Dans cette vidéo, on étudie le phénomène de battement en se basant sur un relevé expérimental représentant une somme de deux signaux sinusoïdaux. La représentation de Fresnel, qui utilise des vecteurs pour représenter l'amplitude et la phase des signaux, permet de comprendre le phénomène. La fréquence de battement est déterminée à partir de la période d'oscillation et la période de battement. Les différences entre les phases des signaux déterminent l'amplitude du signal résultant. Grâce à l'analyse des relevés expérimentaux, les fréquences et amplitudes des signaux sont déterminées. La représentation de Fresnel est un outil utile pour comprendre le phénomène de battement.

Onde progressive

Dans cette vidéo, nous étudions le modèle des ondes progressives harmoniques se propageant dans le sens des X croissant. La forme générale de l'onde est donnée par Eta de X et de T égale à EtaM cosinus de ωT moins kX plus Phi. Nous étudions ensuite les signaux enregistrés par deux capteurs placés à des positions différentes, et identifions leur phase initiale et leur déphasage Delta Phi de 1. Pour que les signaux soient en phase, il faut que Δ Phi de 1 soit égal à k fois 2π, avec k un entier strictement négatif. Pour qu'ils soient en opposition de phase, il faut que la différence de phase entre les deux fasse intervenir un moins devant, avec Δ Phi de 1 égal à 2k plus 1 fois π, et X2 égal à X1 moins k plus 1 demi fois lambda, avec k appartenant à Z privé de n étoiles.

Onde stationnaire et modes propres

Cette vidéo traite des modes propres associés à une onde stationnaire. Un mode propre correspond à une manière naturelle d'osciller pour un système physique, qui dépend des conditions dans lesquelles il se trouve. L'onde stationnaire étudiée est sur une corde et est décrite par la relation y(x,t) = y0 sin(ωt + φ) sin(kx + ψ), où y est la déformation verticale de la corde. Les conditions aux limites en x=0 et x=L permettent de quantifier la fréquence et le vecteur d'onde, qui correspondent au mode propre du système. L'expression du nème mode propre Yn de Xt en fonction de nLc Xt et de l'amplitude de ce mode propre Y0n est donnée. La quantification du vecteur d'onde est un concept important en physique qui se retrouve en mécanique quantique.

Onde stationnaire

La vidéo explique le modèle des ondes stationnaires en montrant que la superposition de deux ondes progressives sinusoïdales de même amplitude et de même pulsation qui se propagent dans des directions opposées donne une onde sinusoïdale. Pour y arriver, il utilise des formules de trigonométrie et montre que la superposition des deux ondes progressives donne une onde stationnaire, qui est une fonction de l'espace et du temps présentée comme le produit d'une fonction uniquement du temps et d'une fonction uniquement de l'espace. Cette première approche du modèle des ondes stationnaires sera développée dans les prochaines vidéos.

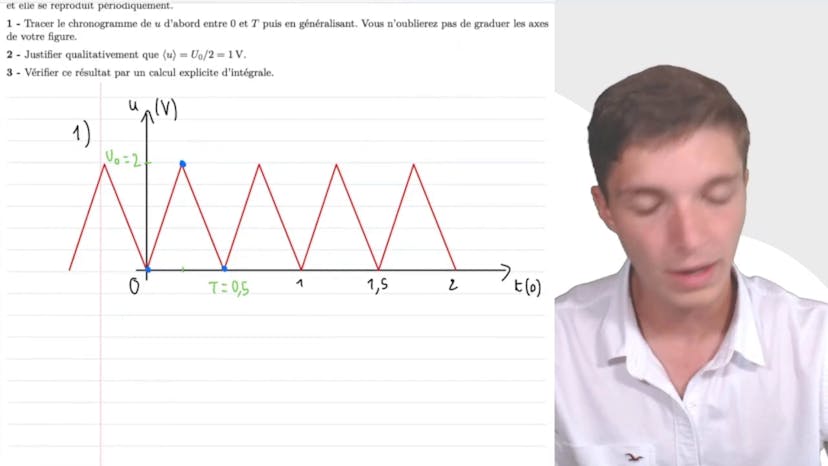
Signal triangle

Dans cette vidéo, nous étudions un signal triangle avec une tension U de t triangulaire comprise entre 0 et U0. Le signal a une période T qui est égal à 0,50s et est défini par une équation. Pour tracer le chronogramme, on voit que le signal augmente de manière linéaire avec une pente de 2U0 sur T avant de diminuer de la même façon pour revenir à 0 lorsque T vaut T. La valeur moyenne de U est équivalente à U0 divisé par 2 et est donc égale à 1V. Cela peut être justifié qualitativement en considérant que chaque temps passé au-dessus de 1V est compensé par la même quantité de temps passé en-dessous de 1V. Cette valeur moyenne peut être calculée en utilisant l'intégrale de la définition de la valeur moyenne d'un signal périodique. Ce signal triangle est très utilisé expérimentalement dans les circuits électriques.