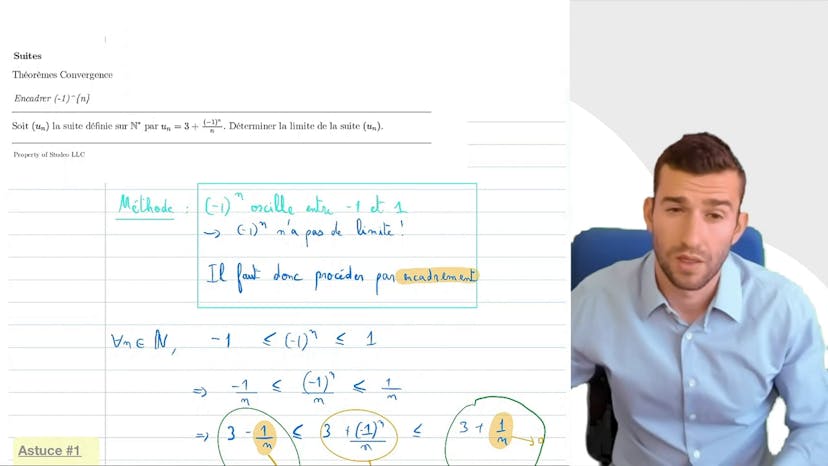Home

Terminale

Maths Spé

Analyse

Théorèmes de Convergence

Dans cette méthode de convergence de suites, on étudie des suites sous forme de fonctions rationnelles, où le degré du numérateur est égal au degré du dénominateur. La limite est le quotient des coefficients dominants de chacun des polynômes. On s'intéresse aux résultats préliminaires comme la majoration, la croissance, et on en déduit la convergence avec les théorèmes de convergence. Pour étudier la monotonie d'une suite, on peut utiliser la méthode du quotient U n+1/U n. On ajoute ensuite les résultats préliminaires pour montrer la convergence. Les exemples présentés montrent comment majorer une suite et déduire la convergence en étudiant la croissance de U n, mais la limite ne sera pas toujours le majorant.

Dans cette dernière méthode, on va revenir au cas que j'avais mentionné à la vidéo 6, où on a une fonction rationnelle, où la suite est sous forme d'une fonction rationnelle de n, et le degré du numérateur est égal au degré du dénominateur, et là, la limite va être le quotient des coefficients dominants de chacun des polynômes, qui constituent le numérateur et le dénominateur. Mais là, on ne va pas s'intéresser à la limite en elle-même, mais aux résultats préliminaires qu'on peut montrer, comme la majoration, la croissance, et en déduire la convergence avec les théorèmes de convergence. Donc là, par exemple, premier exercice, on considère la suite U n égale n-1 sur n plus 4. Donc là, on veut montrer que c'est majoré par 1 dans cette question. Donc là, ça veut dire quoi? Ça veut dire qu'en fait, le numérateur est plus petit que le dénominateur, si c'est plus petit que 1. Une fois qu'on a compris ça, c'est vrai que c'est plutôt facile, on se dit que je pars de moins 1, je dis que moins 1 est plus petit que 4, on rajoute n, et ensuite je fais le quotient. Et comme c'est positive, ça ne change pas le signe, donc j'en déduis que U n est strictement inférieur à 1. Pour étudier la monotonie d'une suite, ensuite on nous demande la monotonie. Là, franchement, tout le temps, quasi tout le temps, c'est U n plus 1 moins U n. Dans de rares cas, on peut faire l'étude du quotient et regarder s'il est plus petit ou plus grand que 1. Mais il faut des conditions pour ça. La première condition, c'est qu'il faut que U n ne s'annule jamais. Et il faut que U n ne change pas de signe. Donc il faut d'abord s'assurer de ça avant d'étudier le U n plus 1 sur U n. Dans quel cas c'est intéressant? C'est quand, d'étudier plutôt le quotient, c'est quand la suite elle-même est constituée de produits de quotient ou des factoriels, par exemple, où ça se simplifie, quand on fait U n plus 1 sur U n. Là, ça peut très bien marcher, parce qu'elle ne change pas de signe, la suite, à part en 0 où elle va être négative. En tout cas, l'important, c'est qu'elle ne change pas de signe à partir d'un certain rang. Puisque la limite, de toute façon, on s'intéresse à ce qui se passe en plus de l'infini. Peu importe si sur les trois premiers termes elle est négative. Donc on pourrait le faire. Finalement, la méthode du U n plus 1 sur U n fonctionne très bien. Donc on fait U n plus 1 sur U n. Là, je fais ma différence. Donc là, je n'ai pas trop le choix, j'ai deux quotients. Je mets tout au même numérateur. Donc je mets tout sur n plus 5, n plus 4. Moi, ça me va, parce que ce que je veux, c'est juste le signe. Donc ce dénominateur, je vois qu'il est positif, n plus 4, n plus 5. Donc ce qui m'intéresse, ça va être juste le signe du numérateur. Là, je développe tout, parce que vraisemblablement, quand je vois ça, je ne peux rien factoriser. Je développe tout et on va voir ce qu'il reste. Donc en fait, je vois que les n carrés sautent. J'ai du 4n plus 5n moins n. Ça aussi, ça saute, ça tombe bien. Et ensuite, j'ai du moins moins 5, n'oublions pas le moins ici. Donc ça fait plus 5. C'est positif. Tout est positif là-dedans. Donc j'en déduis que U n est strictement croissante, strictement positif. Ensuite, U n est croissante et majorée, donc elle est convergente. Le théorème de convergence ne me permet pas de connaître la limite. Je suis juste que c'est convergent, que U n est convergent. Après, comme je vois que c'est incotient, c'est une fonction rationnelle, on a vu la méthode 6 et je peux facilement montrer que ça tend vers 1. Je prends les coefficients dominants de ces deux polynômes. Ici, c'est un 1, c'est 1n moins 1 et 1n plus 4. Donc ça fait 1 sur 1, ça donne 1. Je pourrais donner la limite. Petite remarque, la limite n'est pas forcément le majorant qu'on a trouvé. C'est très important. Je vous donne un exemple ici. Ma fonction est bien croissante, elle est majorée par un réel que j'ai appelé M, mais elle ne tend pas vers M, elle tend vers L. Donc en fait, si on trouve un majorant, ici j'ai trouvé un majorant qui est 1, ça ne veut pas dire que la suite tend vers 1. En l'occurrence, c'est le cas, elle tend bien vers 1, mais je ne peux pas le déduire grâce à mon théorème de convergence. Moi, j'en déduis juste la convergence, mais je ne sais pas vers quoi avec ces théorèmes-là. Donc ça, c'est très important. Deuxième exemple, maintenant, du même style. On a U n égale 2n moins 2 sur n plus 4. Là, c'est pareil, si j'utilise la méthode du 6, je sais que ça va tendre vers 2, cette limite. Je vois que c'est deux polynômes de même degré. Le coefficient dominant ici, c'est 2, ici c'est 1. Faire 2 sur 1, ça va tendre vers 2. Mais ce n'est pas l'objet de l'exercice. L'objet de l'exercice, c'est de montrer d'abord que c'est majoré, étudier les variations de U n et en déduire la convergence. Là, on veut montrer que c'est plus petit que 2. Quand on voit ça, on voit 2n moins 2 sur n plus 4. Là, il faut avoir un peu d'intuition, dire que je vais essayer de faire par majoration successive, et on va voir si ça marche. Des fois, la majoration qu'on a faite est trop grossière. On se dit que ça ne marche pas. Donc, il faut tenter. 2n moins 2, je dis que c'est plus petit que 2n. 2n plus 4, je dis que c'est plus grand que n. Donc, par caution, je prends l'inverse. Je dis que 1 sur n est plus grand que 1 sur n moins 4. Attention ici, je dis que c'est plus grand que 0. Pourquoi? Parce que je vais multiplier les deux inégalités. Moi, ce que je vous conseille, c'est jamais de diviser une inégalité par une autre. Elles ne sont pas dans le bon sens, il faut les inverser. C'est le meilleur moyen de faire une erreur. Le mieux, c'est toujours écrire les inégalités dans le même sens, plus petit que, plus petit que, plus petit que, et de les multiplier entre elles, pas de les diviser, parce que des fois, on oublie d'inverser, etc. C'est très important, parce qu'on sait que la multiplication peut faire changer le signe. C'est pour ça que ce plus grand que 0 ici est capital, parce que je m'assure que les termes ici sont positifs, et quand je vais multiplier cette inégalité-là avec celle-ci, ça ne va pas changer le signe. Attention, 2n-2 pour n égale à 0, ce n'est pas positif. Là, il y a un petit cas à regarder en 0. En tout cas, à partir de 1, c'est bon, c'est positif. Du coup, je peux dire que pour toute n appartenant à n étoiles, j'ai 0 qui est plus petit que 2n-2, qui est plus petit que 2n, 0 qui est plus petit que 1 sur n plus 4, qui est plus petit que 1 sur n, et là, je peux tout multiplier. Donc, ça me fait 2n-2 divisé par n plus 4, qui est plus petit que 2n sur n, qui fait lui-même 2. Donc, j'ai dit que un super inférieur à 2. Ensuite, on s'intéresse au cas en 0, qu'on a dû exclure, mais là, pas de problème, puisque 0, je peux faire le calcul, ça fait moins 1,5, c'est bien plus petit que 2. Donc finalement, au global, j'ai bien pour toute n appartenant à n, un qui est inférieur à 2. Deuxième question, on me demande d'étudier les variations de la suite un. C'est pareil, je vais étudier la différence. J'ai deux quotients. Attention, des fois, je vois l'erreur. Quand un plus 1, c'est tout simplement que je remplace les n par n plus 1. Mais mettez des parenthèses s'il le faut. Donc là, c'est deux fois n plus 1, ça fait 2n plus 2, ça ne fait pas 2n plus 1. Donc quand je développe, ça fait 2n plus 2, je mets tout le même dénominateur, et je développe, un peu comme tout à l'heure, parce que là, je vois que je ne peux rien refactoriser, je développe tout, et je regarde ce qui se supprime. Il y a pas mal de choses qui se suppriment. Il y a le 2n², il y a du 8n, 10n, 2n, tout ça, ça part. Il ne me reste que 10. Donc très bien, tout est positif là-dedans. Tout est strictement positif, et donc ma fonction un est strictement croissante. Idem, qu'est-ce que je sais? J'ai ma suite un qui est majorée, un qui est strictement croissante, donc d'après l'héterogène de convergence, un converge. Mais on ne sait pas vers quelle limite. Je l'ai bien remis ici, une suite croissante majorée ne converge pas forcément vers ce majorant. Elle peut converger vers quelque chose de plus bas. Là, les deux exemples qu'on a faits ne sont pas très représentatifs, parce qu'en l'occurrence, elle converge bien vers 2, ce que je disais tout à l'heure, mais si j'avais montré qu'elle était inférieure à 4, elle converge vers 2. Donc faites bien attention à ça. Voilà, pour ces deux exemples, comme d'habitude, si vous avez des questions, vous pouvez aller dans la FAQ.

Exo TRÈS classique

RELATED

Recommended videos

Intro Convergence

Encadrer sin(n)

Encadrer (-1)^n