All subjects
All subjects
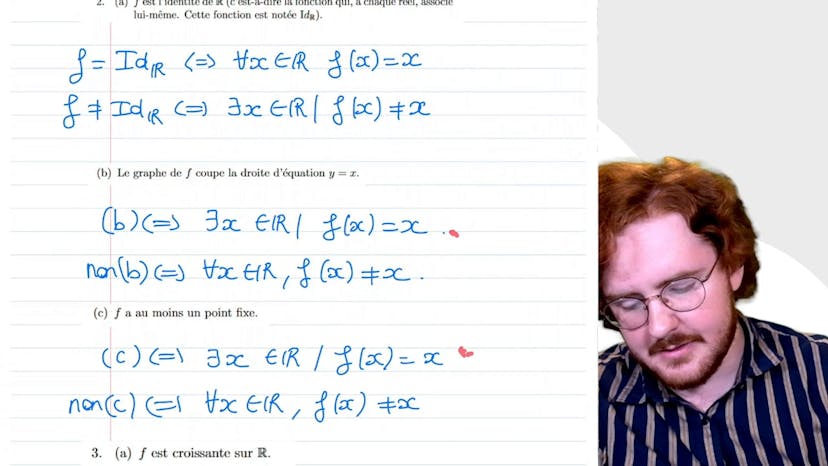
 All subjects
All subjects
Langage binaire
Dans cette vidéo, Paul explique comment démontrer que pour tout entier n supérieur ou égal à 1, cet entier peut s'écrire comme la somme de puissances de 2 toutes distinctes. Il propose d'utiliser la récurrence forte pour prouver cette propriété. Il montre que pour k appartenant à 1n, k peut s'écrire comme la somme de puissance de 2 toutes distinctes en utilisant la décomposition de p, un nombre inférieur ou égal à n. Si n+1 est paire, l'idée est de trouver un nombre p et d'ajouter 1 à toutes les puissances de 2 de sa décomposition pour prouver que n+1 peut s'écrire comme une somme de puissances de 2 distinctes. Si n+1 est impaire, il suffit de réutiliser la décomposition de p pour montrer que n+1 peut s'écrire comme une somme de puissances de 2 distinctes. Ainsi, pour toute entière n supérieure ou égale à 1, on peut s'écrire comme une somme de puissances de 2 distinctes.