Home

MPSI/PCSI

Maths

Analyse

Continuité sur un segment

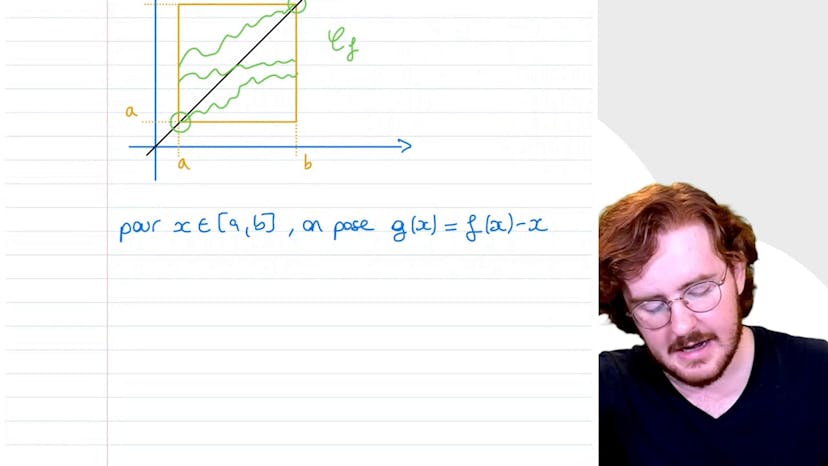
Dans cette vidéo, Paul aborde le lien entre continuité, bijection et fonctions. Il considère la fonction f de x égale à 1 plus exp de x, sur le domaine R. Il montre que f est une bijection de R sur son image, en utilisant le théorème de la bijection, la continuité et la stricte croissance de f. Il détermine ensuite le domaine d'arrivée et la bijection réciproque en résolvant l'équation f de x est égal à y, et trouve que l'image de R par f est R plus étoile. Il donne l'expression de la bijection réciproque f moins 1 de y est égal à logarithm 2 exponentielle de y moins 1.

Salut c'est Paul, on se retrouve pour une nouvelle vidéo où on va aborder le lien entre continuité, bijection et ce genre de choses. L'exercice consiste en deux questions sur la fonction de R dans R définie par f de x égale le gain de 1 plus exp de x, qui est 1 plus exp de x, 1 c'est toujours strictement positif, donc cette fonction est bien définie. Il faut montrer que f réalise une bijection de R sur son image. Pour ça on va utiliser le théorème de la bijection. Pour utiliser le théorème de la bijection, on doit avoir deux choses, que f soit continue, donc là c'est bien le cas, et que f soit strictement croissante, donc pour ça on va utiliser la dérivée de f. On a x qui donne 1 plus exp de x dérivable et strictement positif sur R, le gain de x est dérivable sur R+, donc f est dérivable sur R par composition, et on a sa dérivée qui est composée d'exponentielle ici et là, et elle est strictement positive de manière évidente, donc f est strictement croissante et continue, ce sont ces deux mètres de définition, et donc là on a la stricte croissance et la continuité, parce qu'on a la dérivabilité donc continuité, et donc d'après le théorème de la bijection, f réalise une bijection de R dans son image. Maintenant qu'on sait que f réalise une bijection, on va déterminer le domaine d'arrivée et la bijection réciproque. Une astuce c'est qu'on le fait les deux en même temps en résonnant par équivalence, donc il faut un peu intuiter ce que ça va être f de R pour ça, f de R, là, le gain de x quand x tend vers moins l'infini, l'exponentielle de x tend vers 0, donc le gain ici ça tend vers 1, et donc le gain de x tend vers moins l'infini, tend vers 0 pardon, en plus l'infini, tout tend vers plus l'infini, ainsi j'intuite que le domaine de définition c'est R plus étoile, enfin le domaine d'arrivée, donc l'image de R par f, ce soit R plus étoile. Donc on prend un y dans R plus étoile, je le nomme y parce que f de x est égal à y, et on va résoudre l'équation f de x est égal à y, donc c'est équivalent à logarithm 2, j'aurai écrit ce que ça veut dire, et comme l'exponentielle est une bijection, on peut appliquer l'exponentielle des deux côtés de l'égalité et on conserve l'équivalence. Comme logarithm est une bijection, on peut appliquer logarithm des deux côtés de l'égalité, on est bien sur le domaine de définition des deux côtés, et conserver l'équivalence. Ainsi on a trouvé un antécédent à y, et vu qu'on a l'équivalence, on a l'unicité de cet antécédent et l'existence. Donc quel que soit y appartenant à R plus étoile, f moins 1 de y est égal à logarithm 2 exponentielle de y moins 1. Donc on a l'existence et l'unicité de l'antécédent, ce qui nous donne l'image de R par f, donc qui est bien R plus étoile, et en même temps ici on a la bijection acéproque. Donc f moins 1 de y est égal à logarithm 2 exponentielle de y moins 1, pour toute y dans R plus étoile. Voilà, c'est la fin de cet exercice, et on se dit à la prochaine fois!

Bijection réciproque

RELATED

Recommended videos

Variations et théorème des valeurs intermédiaires

Point fixe et continuité

Fonction bornée