Home

MPSI/PCSI

Maths

Analyse

Continuité sur un segment

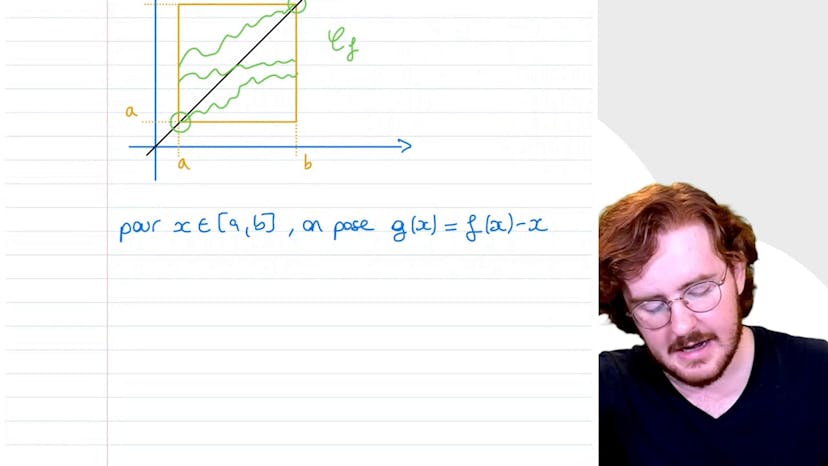
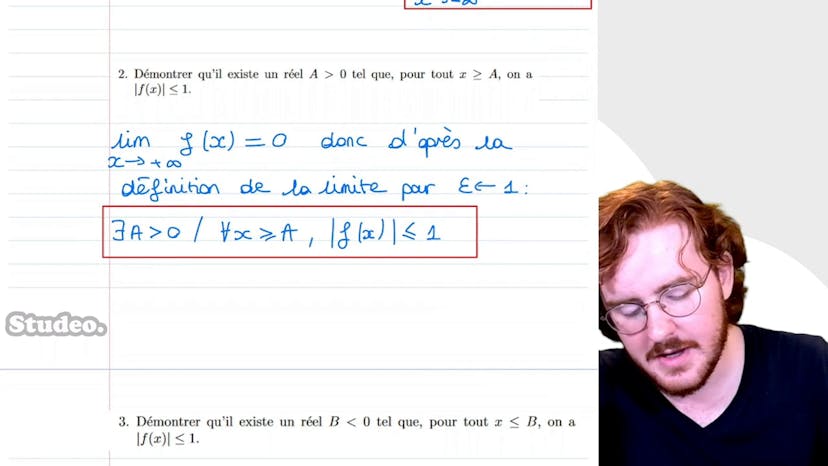
Dans cette vidéo, on étudie la fonction f définie par f(x) = x-2 + log(x) sur l'intervalle des réels positifs. On montre que f réalise une bijection de R+* dans R en montrant sa stricte croissance et sa continuité. On étudie ensuite sa bijection réciproque g, démontrant qu'elle est aussi une bijection. On prouve que la limite de g en moins l'infini est égale à zéro en utilisant le théorème de la limite monotone. On trouve également que l'équation f(x) = 0 possède une unique solution alpha dans R+*. Enfin, on détermine la limite de f(x)/x en trouvant un équivalent de g au voisinage de plus l'infini et en utilisant la composition des limites.

Salut c'est Paul, et bienvenue dans cette nouvelle vidéo où on va parler de continuité, bijectivité et application réciproque. Donc on a une fonction f définie comme étant la fonction qui s'associe à x, x-2 plus logarithm de x, et qui est définie sur r plus étoile, parce qu'on a un logarithm ici. Et on va montrer d'abord que f réalise une bijection de r plus étoile sur r, et étudier l'application réciproque de g avec toute continuité et monotonie limite aux bornes de l'intervalle, donc la base des études de fonction. Donc comment on va montrer que f réalise une bijection? C'est très simple. On a la forme explicite de f, et c'est une fonction facile à interpréter, c'est des fonctions usuelles. Donc on utilise le terme de la bijection, on va montrer la stricte monotonie. Donc f est strictement croissante et continue sur r plus étoile, par somme de fonctions strictement croissantes et continue sur r plus étoile. Là il n'y a pas besoin de la dérivée. Donc f réalise une bijection de r plus étoile dans f de r inclus dans r. Et on a qu'en plus infini la limite est égale à plus infini, et en zéro la limite est égale à moins infini. Donc par continuité de f, l'image de r plus étoile par f est bien r. Donc on a bien que f réalise une bijection de r plus étoile dans r. Maintenant on va étudier la bijection réciproque de f qu'on nomme g. Donc f est continue et strictement croissante. Pourquoi je dis ça? Parce que f moins 1 de g égale g, et donc continue aussi et est strictement croissante. C'est une propriété de la réciproque. C'est le piège de partir des cèdres de partiels de choses compliquées. C'est juste parce que c'est la bijection réciproque. Elle conserve la continuité et la stricte croissance. Elle est strictement monotone aussi et elle a la même monotonie. Donc g est une bijection, la bijection réciproque est aussi une bijection, c'est dans le nom, de r dans r plus étoile. Donc g est minoré par zéro et non majoré. Alors là en fait, par où je pars, je vais expliquer, on part pour trouver ce qu'il nous manque, c'est les limites aux bornes de l'intervalle de g, donc en plus l'infini et moins l'infini. Donc là, j'utilise le fait que g est sous la bijection de r dans r plus étoile. Donc g est minoré par zéro et non majoré, parce qu'elle arrive dans r plus étoile tout entier. Et g est strictement croissante, on l'a démontré jusqu'à présent, mais je le rappelle. Donc d'après le théorème de la limite monotone, on a que la limite en plus l'infini de g de x est égale à plus l'infini, parce que stricte croissance et non majoré. Et la limite en moins l'infini, c'est égal à g de x, c'est égal à une limite supérieure égale à zéro, parce qu'elle va dans r plus étoile, g, et elle est minorée par zéro. Donc toujours par le théorème de la limite monotone, et on va prouver que cette limite est bien zéro, parce que si elle est strictement supérieure à zéro, par l'absurde, on peut trouver un l sur 2 ici, tel que g n'atteindra jamais ce l sur 2. Parce que d'après le théorème de la limite monotone, g approche la limite par la stricte croissance de g, g approche la limite par valeur supérieure ici, donc n'atteint jamais ce domaine ici. Et ainsi, ça contredit la bijectivité de r dans r plus étoile. Ainsi, la limite de g en moins l'infini, c'est égal à zéro. Et donc, on a bien tout répondu à la question sur les propriétés de g. Maintenant, on va montrer que l'équation f de x égale à zéro, elle met une unique solution dans r plus étoile notée alpha. F de x égale à zéro, c'est la définition de la bijectivité de r plus étoile dans r. Tout simplement, c'est par définition, et qu'on a prouvé que f était bijectif de r plus étoile dans r. F de x égale à zéro possède une solution alpha appartient à r plus étoile. Maintenant, on va étudier la limite de f de x sur x, et on va en déduire une limite sur f de g de t sur g de t, puis un équivalent de g au voisinage de plus d'infini. D'abord, f de x sur x, on connaît f, donc, qu'il que soit x qui est équivalent au spéromètre zéro, on calcule ce que ça fait f de x sur x, ça fait 1 moins 2 sur x plus log m de x sur x. Et là, on étudie les limites. Par croissance comparée, log m de x sur x tend vers zéro. Le x l'emporte sur le log m de x. Ainsi, la limite qu'on cherchait, c'était 1. Maintenant, on va remarquer que la limite de g de t, comme on l'a vu plus précédemment, en plus l'infini, c'est plus l'infini. Et que g de r s'égale à r plus étoile. On peut composer les limites, parce que l'image de g est à valeur dans le domaine de décision de f. Ainsi, on peut composer des limites. La limite pour t tend vers plus l'infini de f de g de t sur g de t est égale à 1. On remplace le x par le g de t. Or, on doit trouver un équivalent de g en plus l'infini. On va utiliser la définition par la limite de l'équivalent. La limite de g sur l'équivalent, enfin, l'équivalent sur g est égale à 1. On va essayer de remplacer ce f de g de t. On remarque que f de g de t, pour quelque chose qui appartenant à r, s'égale à t, parce que g est la bisection assez proche de f. Ainsi, on a que cette limite ici, c'est la limite de t sur g de t, c'est égale à 1. Et donc, c'est bien la définition que g est équivalent à t en plus l'infini. C'est la fin de cet exercice, et on se dit à la prochaine fois!

Équivalent d'une bijection réciproque

RELATED

Recommended videos

Variations et théorème des valeurs intermédiaires

Point fixe et continuité

Fonction bornée