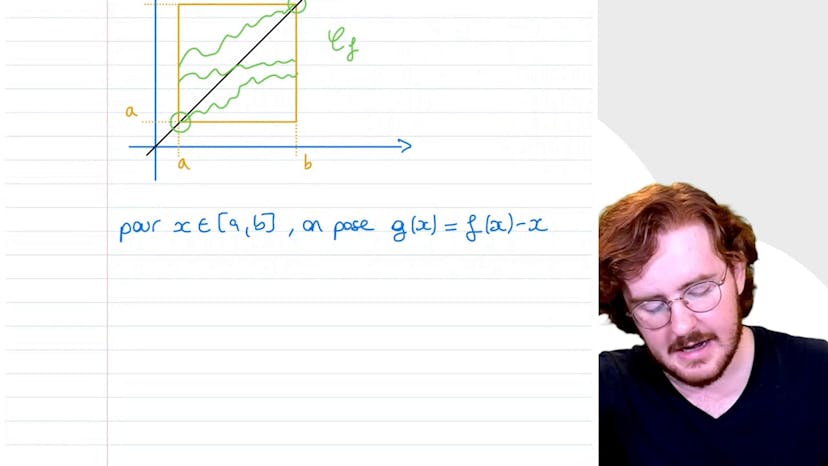
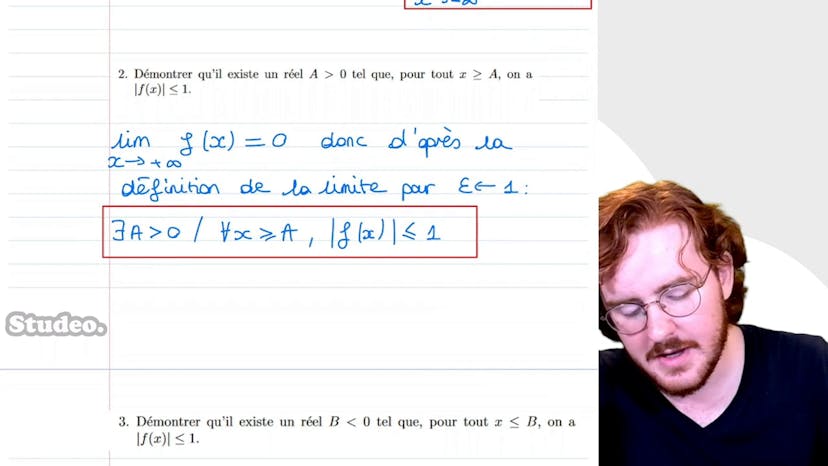
All subjects
All subjects
 All subjects
All subjects
Continuité et température terrestre
Dans cet exercice, nous cherchons à prouver qu'il existe toujours deux points sur l'équateur ayant la même température. Pour ce faire, nous considérons la température comme une fonction continue de la longitude, T(x), qui est périodique de période 2π. Nous cherchons donc à trouver un x tel que T(2x) = T(2x+π), ce que nous traduisons en T(2x) - T(2x+π) = 0. Nous posons la fonction f(x) = T(2x) - T(2x+π), qui est continue et périodique, et cherchons deux points, x0 et x1, tels que f(x0) > 0 et f(x1) < 0. En utilisant la périodicité de T, nous trouvons x1 = x0+π tel que f(x1) = T(2x1+π) - T(2x1) = -f(x0). Nous appliquons le théorème des valeurs intermédiaires pour conclure qu'il existe un x2 sur l'équateur tel que T(2x2) = T(2x2+π), prouvant ainsi notre hypothèse initiale.