Home

MPSI/PCSI

Maths

Analyse

Continuité sur un segment

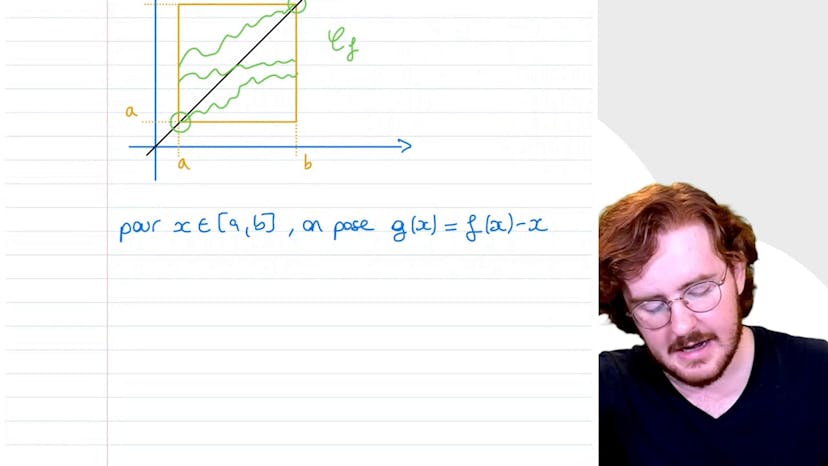
Dans cet exercice de mathématiques, Paul montre comment prouver la continuité d'une fonction croissante sur un segment AB. En utilisant un dessin pour mieux visualiser, Paul illustre que la fonction croissante f doit être continue sur le segment AB pour que l'image par f du segment AB soit égale au segment f2 à f2B. Pour prouver la continuité, Paul utilise la technique de la réduction à l'absurde et montre que si f était non continue en x0, cela entraînerait une contradiction. En utilisant le théorème de la limite monotonale et les inégalités fournies par la croissance de f, Paul montre qu'il existe un alpha compris dans le segment L- L+, qui est non vide et n'appartient pas à f2 AB, ce qui contredit l'hypothèse initiale. Ainsi, f est continue sur le segment AB.

Salut c'est Paul et on se retrouve pour un nouvel exercice sur la continuité. Donc là on a f, une fonction croissante sur le segment AB tel que l'image par f du segment AB est égale au segment f2 à f2B. Et on va devoir montrer ici que f est continue sur ce segment AB. Donc là moi je vais bien faire un dessin. La continuité c'est bien de faire des dessins, tout ça pour visualiser bien tous les quantificateurs. C'est bien de visualiser. Et donc qu'est ce que ça veut dire? f croissante sur AB tel que ceci. En fait l'image du segment AB ici est égale au segment f2 à f2B. Et f est croissante donc je sais que f2 à f2B sont bien dans le même ordre que A et B. Et ça veut dire que le graph de f est compris dans ce rectangle ici. Et donc si je trace f, donc f est croissante, si je trace f ici elle est continue. Imaginez qu'elle soit discontinue. Ici on voit bien que ce morceau du segment f2 à f2B n'a pas d'antécédent par f. Et la seule manière pour qu'il en ait, et que f soit continue, c'est que ici ça reprenne et là ça reprenne en bas par exemple. Mais là on casse la croissance. Donc c'est comme ça qu'on va faire, on va soit casser la croissance, soit casser le fait que l'image soit égale à f2 à f2B. Et donc la bonne manière de le faire soit par l'absurde. C'est parti. Donc on va supposer qu'il existe un x0 appartenant A à B tel que f est non continue en x0. Et donc quand on aura la négation ça nous donnera que f est continue en toute x0. Et donc là on va la supprimer sur A. Comme f est croissante et bornée sur A et B, les limites suivantes existent et sont finies. D'après le théorème de la limite monotonale. C'est ça qui est important, le fait que f soit sur le segment. Donc la limite de f2x quand x tend vers x0 par valeur négative c'est égale à L-. Et elle est différente de la limite de f2x quand x0 tend vers valeur plus taille. Elle est différente de la limite de f2x quand x0 tend vers valeur plus positive L+. Parce que sinon on aurait la continuité en x0. Et on a bien f non continue en x0. Et par croissance de f et en utilisant l'inégalité fournie par le fait que f soit croissante et en passant à la limite. On a que quel que soit x appartenant à A x0, f2x est inférieur ou égal à L-. Et quel que soit x appartenant à x0 A, f2x est supérieur ou égal à L+. Et en fait là, entre L+, L- qui sont différents les uns des autres. On a qu'il existe un alpha ici compris dans le segment L- L+, qui est non vide par croissance et le fait que les deux limites sont différentes. Il existe un alpha tel que alpha n'appartient pas à f2 AB. J'ai re-écrit ce qu'on avait vu un peu sur le schéma. Et donc alpha n'appartient pas à f2 AB. Or alpha appartient au segment AB, parce que alpha appartient à L- L+, qui sont eux-mêmes compris dans AB. D'où une contradiction. Ainsi f est continu sur le segment AB. Voilà, c'est la fin de cet exercice et on se dit à une prochaine fois!

Ensemble image et continuité

RELATED

Recommended videos

Variations et théorème des valeurs intermédiaires

Point fixe et continuité

Fonction bornée