Online Physique-Chimie Courses by Top Instructors

Équation de réaction

Dans cette vidéo, Mathis explique comment écrire une équation de réaction en électrochimie. Il mentionne que lors d'une électrolyse, les réactions électrochimiques aux électrodes sont les suivantes : le nickel solide donne Ni²+ et deux électrons, et le Zn²+ donne Zn solide et deux électrons. Pour écrire l'équation de la réaction d'électrolyse, il faut combiner linéairement les équations de manière à égaler le nombre d'électrons de part et d'autre. On souhaite que dans l'équation finale, il n'y ait pas d'électrons qui interviennent. En sommant les deux équations, on obtient deux électrons de chaque côté, ce qui permet de les supprimer. L'équation finale est donc Ni solide plus Zn²+ est égal à Ni²+ plus Zn solide. Cette équation est parfaitement équilibrée. Peu importe la manière dont on combine linéairement les équations, on obtiendra toujours une équation équilibrée qui décrit la réalité chimique de ce qui se passe dans la pile. Il est important de comprendre qu'il faut combiner linéairement les différentes équations pour compenser le nombre d'électrons produits ou consommés de chaque côté.

Raisonnement inverse

Dans cette vidéo, on aborde la réaction d'électrolyse d'une solution de chlorure de fer 3 : 2Cl- + 2Fe3+ + eau -> Cl2 + 2Fe2+ + eau. Pour écrire les demi-équations électrochimiques et les couples d'oxydoréduction, on introduit artificiellement un nombre d'électrons. On remarque que la charge varie de 2 lorsqu'on passe d'une espèce à l'autre. Ainsi, on introduit 2 électrons de chaque côté pour équilibrer la charge. On sépare ensuite les deux équations : 2Cl- -> Cl2 + 2e- et 2Fe3+ + 2e- -> 2Fe2+. Simplifiées, les équations deviennent Fe3+ + e- -> Fe2+ et Cl2 + 2e- -> 2Cl-. Les couples d'oxydoréduction associés sont Fe3+/Fe2+ et Cl2/Cl-. Cette approche inversée de l'électrolyse permet de mieux comprendre les phénomènes chimiques impliqués. Merci d'avoir suivi cette vidéo et à bientôt !

Spontannée ou forcée ?

Dans cette vidéo, Mathis explique comment déterminer si une réaction chimique évolue de manière spontanée ou forcée. Il présente une équation chimique formelle impliquant A, Aq, Bq, CAq et D. La constante d'équilibre à 25°C est de 2,8x10^4 et le quotient de réaction initiale est de 10. Pour déterminer le sens d'évolution de la réaction, il compare le quotient de réaction avec la constante d'équilibre. Si le quotient de réaction est inférieur à la constante d'équilibre, la réaction évolue dans le sens direct, où A et B sont des réactifs pour former C et D. Si le quotient de réaction est supérieur à la constante d'équilibre, la réaction évolue dans le sens inverse, où C et D réagissent pour former A et B. Il est également possible de forcer la réaction à évoluer dans le sens inverse en apportant de l'énergie, comme dans le cas des batteries rechargeables. Cependant, cela nécessite un apport d'énergie, souvent sous forme électrique.

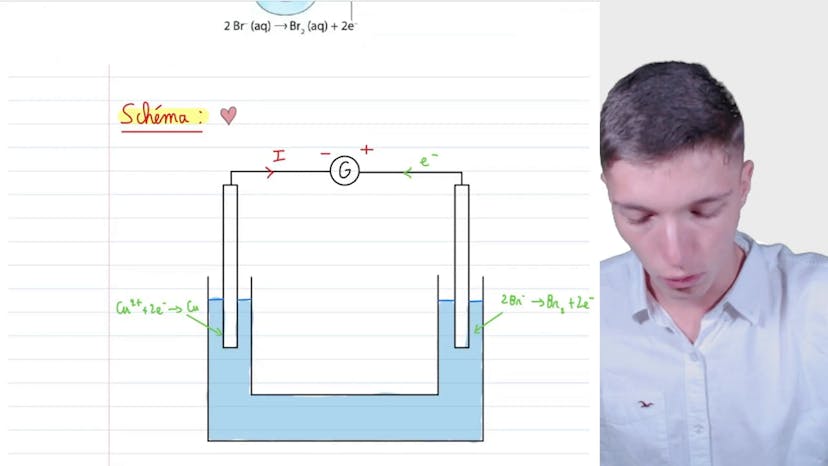
Schéma d’électrolyse

Dans cette vidéo, nous apprenons le schéma classique d'un électrolyseur pour la solution de bromure de cuivre 2. Nous devons recopier et compléter le dispositif relatif à l'électrolyse, en précisant les branchements du générateur, le sens conventionnel du courant et le sens de déplacement des électrons. Les deux électrodes du dispositif sont présentées, avec les réactions qui se produisent à chaque électrode. Le sens de déplacement des électrons peut être déterminé en observant si les électrons sont consommés ou produits à chaque électrode. Dans le cas présent, les électrons sont émis au niveau de l'électrode de gauche et consommés à l'électrode de droite. Le sens de déplacement du courant est donc inverse à celui des électrons. Les branchements du générateur sont indiqués, avec le courant se déplaçant du plus vers le moins. En suivant cette méthodologie, un schéma clair et compréhensif peut être construit pour l'examinateur ou pour le bac. Merci d'avoir suivi cette vidéo et à bientôt !

Dépôt de cuivre

Aucun résumé n'est disponible pour cette vidéo

Dépôt d’argent

Dans cette vidéo, l'auteur explique le processus d'un dépôt d'argent sur une statuette métallique à l'aide d'un électrolyseur. Les réactions se produisant à chaque électrode sont les suivantes: - À l'électrode en argent: Ag+ + e- -> Ag (oxydation de l'ion argent en argent solide) - À l'électrode en graphique: 2H2O -> O2 + 4H+ + 4e- (oxydation de l'eau en dioxygène) L'équation de la réaction d'électrolyse est obtenue en combinant linéairement les demi-équations. Dans ce cas, elle est donnée par: 4Ag+ + 2H2O -> 4Ag + O2 + 4H+ Ensuite, l'auteur aborde la quantité d'électricité Q qui a traversé l'électrolyseur pendant une durée de 15 minutes, avec une intensité du courant constante à 80 mA. Il explique qu'il y a deux façons d'exprimer la charge débitée par une pile: la vision chimique, où la charge est égale au nombre de molles d'électrons échangés multiplié par le faraday (F), et la vision électrique, où la charge est égale à l'intensité du courant multipliée par la durée d'électrolyse. Dans ce cas, la charge est de 72 coulombs. Ensuite, l'auteur répond à la question sur la quantité de matière d'argent déposée sur la statuette. Il explique qu'il faut relier le nombre de molles d'électrons échangés au nombre de molles d'argent. Il utilise la relation Q = nE * F, où nE est le nombre de molles d'électrons échangés, E est la charge d'une molle d'électrons et F est le nombre d'Avogadro. Il conclut que le nombre de molles d'argent déposé est de 7,5 x 10^-4 molles, ce qui correspond à une masse de 80 mg en multipliant par la masse molaire. Enfin, l'auteur aborde la question du volume de gaz formé, en particulier le dioxygène. Il explique que le nombre de molles d'électrons échangés peut être lié au nombre de molles de dioxygène formé. Il utilise la relation nO2 = nE / 4, où nO2 est le nombre de molles de dioxygène formé. En considérant le dioxygène comme un gaz parfait, il peut relier le nombre de molles d'O2 au volume du gaz en utilisant la relation V = nO2 * R * T / P, où V est le volume, R est la constante des gaz parfaits, T est la température et P est la pression. Il conclut que le volume de dioxygène formé est de 4,6 mL pour une pression de 1 bar et une température de 298 K. En résumé, cette vidéo explique le processus d'un dépôt d'argent sur une statuette métallique à travers l'utilisation d'un électrolyseur. Elle aborde les réactions électrochimiques qui se produisent à chaque électrode, la quantité d'électricité traversant l'électrolyseur, la quantité de matière d'argent déposée et le volume de gaz formé.

Eau de Javel

Dans cette vidéo, on aborde la fabrication de l'eau de Javel, en particulier la production de l'ion hypochlorite Cl-. Cette fabrication se fait par électrolyse d'une solution aqueuse de chlorure de sodium Na+ Cl-. Les électrodes utilisées sont en graphite inerte. Sur l'anode, du dichlore gazeux (Cl2) se forme, tandis que sur la cathode, de l'eau (H2O) réagit pour produire du dihydrogène (H2). Pour la première question, on doit écrire la demi-équation de la réaction sur l'anode et en déduire l'équation de la réaction d'électrolyse. La demi-équation sur l'anode est : 2Cl- = Cl2 + 2e-. En sommant cette équation avec celle sur la cathode, qui est donnée, on obtient l'équation d'électrolyse : 2H2O + 2Cl- = Cl2 + H2 + 2OH-. Pour la deuxième question, il faut faire un schéma du montage en précisant le sens de circulation des porteurs de charge. L'anode est à droite et la cathode est à gauche. À l'anode, l'oxydation se produit, avec la libération de Cl2 gazeux. À la cathode, la réduction se produit, avec la formation de H2 gazeux. Les électrons sont libérés à l'anode et consommés à la cathode. Ainsi, le sens de déplacement des électrons est de la droite vers la gauche, et le sens de déplacement du courant est inversé, de la gauche vers la droite. Enfin, pour la troisième question, on nous demande d'écrire l'équation d'oxydoréduction correspondant à la réaction du dichlore avec lui-même. On équilibre les demi-équations des deux couples redox (Cl2/Cl- et Cl-/Cl2) et on les combine. On obtient donc l'équation bilan : 2Cl2 + 2H2O = 2Cl- + 2Cl- + 4H+. Cette réaction montre comment le dichlore agit à la fois comme oxydant et comme réducteur sur lui-même. En résumé, cette vidéo explique le processus de fabrication de l'eau de Javel par électrolyse d'une solution de chlorure de sodium. Les différentes réactions, les équations et le schéma du montage sont détaillés.

Loi horaire

Dans cette vidéo, nous travaillons sur les lois horaires de la vitesse. On nous donne une bille et les équations de son mouvement en fonction du temps. Le but est d'analyser le vecteur vitesse et le vecteur accélération pour en tirer des informations intéressantes. Tout d'abord, nous devons trouver l'expression des coordonnées cartésiennes du vecteur vitesse de la bille. Pour cela, nous utilisons le lien entre la vitesse et la position, qui est que la vitesse est la dérivée de la position. En dérivant les lois horaires, nous obtenons que la vitesse en x est égale à 0 et la vitesse en y est égale à -9,8t+4. Nous regroupons ces expressions en colonne pour obtenir le vecteur vitesse. Ensuite, nous devons trouver la même chose pour l'accélération. L'accélération est la dérivée de la vitesse, donc nous devons trouver les dérivées de la vitesse en x et en y. Cela nous donne une accélération constante de 0 en x et de -9,8 en y. Ensuite, nous passons à une deuxième bille. Nous devons déterminer graphiquement les expressions de Vx et Vy en fonction du temps. Pour Vx, nous voyons sur le graphique qu'il s'agit d'une constante égale à 2. Pour Vy, nous avons une fonction linéaire, donc nous devons trouver l'ordonnée à l'origine (4) et le coefficient directeur (10). Cela nous donne Vy = -10t+4. Enfin, nous devons également déterminer l'accélération. Nous utilisons la même formule que précédemment, avec A étant la dérivée de V par rapport à T. En dérivant les expressions trouvées précédemment, nous obtenons une accélération de 0 en x et de -10 en y. J'espère que ce résumé vous a été utile. N'hésitez pas à poser vos questions en commentaire.

Voiture

Dans cette vidéo, Leïla aborde les lois de la physique appliquées à une voiture en mouvement. Elle commence par expliquer les forces qui agissent sur la voiture : le poids, la réaction de la route et la force de frottement de l'air. Elle rappelle ensuite la deuxième loi de Newton, qui dit que la variation du vecteur quantité de mouvement d'un système est égale à la somme des forces extérieures appliquées. Elle précise que cette loi s'applique dans ce cas. Leïla explique ensuite qu'il est nécessaire de définir le système, qui est la voiture dans ce cas, et de le considérer comme un point pour faciliter l'analyse. Elle montre que le vecteur quantité de mouvement est égal à la masse de la voiture multipliée par sa vitesse, et que sa dérivée par rapport au temps est égale à la masse multipliée par l'accélération. En utilisant cette loi de Newton, elle démontre que la réaction de la route et le poids se compensent, permettant à la voiture de rester sur la route. Elle souligne que ce qui nous intéresse est la composante horizontale des forces, qui est la force de frottement de l'air. En utilisant les projections des forces selon les axes, elle détermine que l'accélération de la voiture selon l'axe horizontal est égale à moins la force de frottement divisée par la masse de la voiture, soit -0.33 m/s². Leïla conclut en expliquant que pour que la voiture avance dans la bonne direction, il faut compenser les frottements en ajoutant la puissance du moteur, qui va pousser la voiture dans la direction voulue. Elle encourage les spectateurs à poser leurs questions dans les commentaires. Dans ce résumé SEO friendly, nous avons pris en compte les mots clés "physique", "voiture", "lois de la physique", "dynamique", "force", "poids", "réaction de la route", "frottement", "vecteur quantité de mouvement", "système", "moteur", "accélération", "vitesse", "mouvement", "masses", "forces extérieures", "terminale", "projections" et "commentaires".

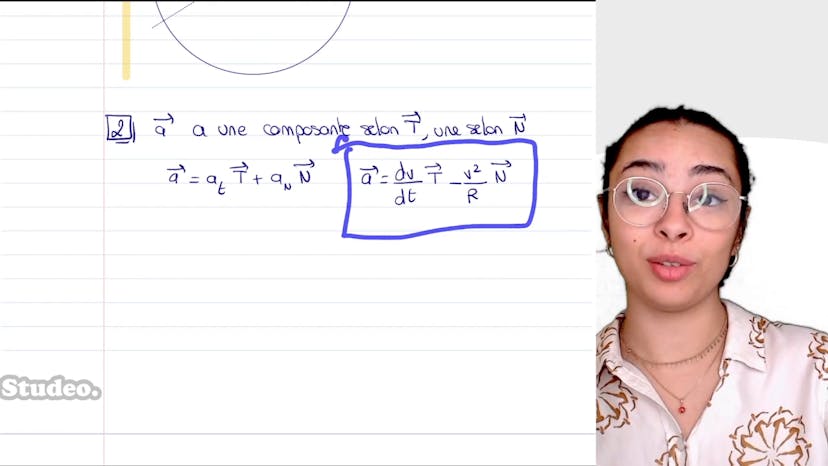
Repère de Frenet

Aujourd'hui, nous allons parler du repère de Freinet. Le repère de Freinet est un repère circulaire utilisé pour représenter les mouvements circulaires ou en forme d'ellipse. Il se compose d'un vecteur N, qui est centripète et dirigé vers le centre du cercle, et d'un vecteur T, qui est tangent au cercle. Cette représentation permet de décomposer n'importe quelle accélération en composantes selon N et selon T. Pour trouver les coordonnées du vecteur accélération A dans ce repère, on utilise la formule générique : A = dv/dt selon T - v²/r selon N, où dv/dt est la dérivée de la vitesse par rapport au temps selon T, v est la vitesse et r est le rayon du cercle. Ensuite, on nous demande si le mouvement est uniforme. Si le mouvement est uniforme, cela signifie que la vitesse est constante, donc dv/dt est nul. Dans ce cas, l'accélération A serait uniquement selon N. Cependant, dans le schéma donné, on peut voir que l'accélération a également une composante selon T, ce qui signifie que le mouvement n'est pas uniforme. J'espère que ce résumé vous a été utile. N'hésitez pas à poser vos questions dans les commentaires.

Trajet orthodromique

Dans cette vidéo, nous nous intéressons à un trajet orthodromique. L'orthodromie correspond à la route la plus courte entre deux points, formant un arc de cercle. Pour déterminer si un trajet est orthodromique, nous devons convertir les différentes valeurs données. Tout d'abord, nous devons qualifier la trajectoire dans le référentiel géocentrique, qui est centré sur la Terre. Si la trajectoire est parcourue à vitesse constante, le mouvement sera circulaire et uniforme. Ensuite, nous devons trouver la valeur d'un mille-marin, qui est de 1 852 mètres environ. Cette information peut être trouvée sur Internet. Enfin, nous devons déterminer si le trajet du skipper Francis Jolion est orthodromique. Pour cela, nous devons convertir la distance en milles marins et la vitesse en noeuds. Un noeud correspond à un mille-marin par heure. L'aspect le plus important de cet exercice est de faire attention aux conversions. Il est nécessaire de convertir les unités correctement pour obtenir les valeurs souhaitées. Une fois toutes les conversions effectuées, nous pouvons calculer la distance parcourue par le skipper à l'aide de la formule de mécanique v x t. Cette distance est de 4367 milles marins. En comparant cette distance à la distance à vol d'oiseau entre les deux villes, qui est de 3452 milles marins, nous pouvons conclure que le trajet du skipper n'est pas orthodromique. Il a donc parcouru une distance supérieure à la route la plus courte. N'hésitez pas à poser vos questions en commentaire sur les conversions ou d'autres aspects abordés dans la vidéo. J'espère que ce résumé répond à vos attentes en termes de référencement SEO.