Online Révisions Maths lycée Courses by Top Instructors

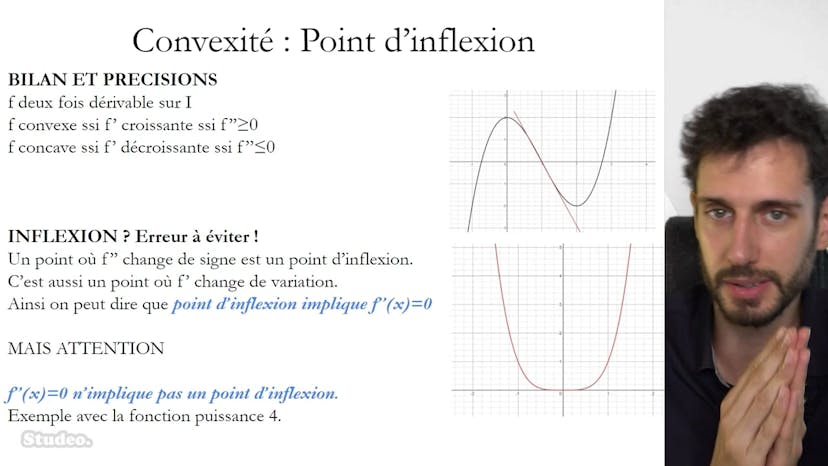
Point d'inflexion

Le cours traite de la notion de point d'inflexion dans les fonctions. Un point d'inflexion est défini comme un point où la courbe de la fonction traverse sa tangente. Visuellement, cela correspond à un changement de comportement de la fonction entre concavité (courbe en haut des sécantes) et convexité (courbe en bas des sécantes), ou vice versa. Un point d'inflexion est également un point de pente maximale de la tangente, où la pente atteint un maximum en valeur absolue. Le cours rappelle également une erreur courante : un point où la dérivée seconde est égale à zéro n'est pas forcément un point d'inflexion, il faut qu'il y ait un changement de comportement de la fonction. Finalement, le cours présente une relation entre la convexité de la fonction et le signe de sa dérivée première : une fonction est convexe si et seulement si sa dérivée première est croissante et positive, et elle est concave si et seulement si sa dérivée première est décroissante et négative.

Démo inégalité convexité

Le cours consiste en la démonstration que le point M, situé entre les points A et B, se trouve également sur la droite AB. Pour cela, le professeur utilise l'équation de la droite AB (Y = AlphaX + Beta) où Alpha est le coefficient directeur et Beta est l'ordonnée à l'origine. Il prouve ensuite que le point M appartient bien à cette droite en remplaçant les coordonnées de M dans cette équation. Si le résultat est égal à l'ordonnée de M, cela signifie que M est sur la droite. En conclusion, puisque le segment AB est au-dessus de la courbe CF (où F est une fonction convexe), l'image de l'ordonnée de M par la droite AB est au-dessus de son image par F.

Démo au programme : convexité et f''

Ce cours aborde les propriétés graphiques et le lien entre la dérivée seconde et la convexité d'une fonction. Si la dérivée seconde d'une fonction f est positive sur un intervalle i, alors la courbe représentative de f est au-dessus de ses tangentes sur cet intervalle. La démonstration consiste à mettre tout du même côté de l'équation de la tangente, poser une fonction qui compare la courbe avec la tangente, et étudier les variations de cette fonction. En montrant que cette fonction est positive ou nulle sur l'intervalle i, on conclut que la courbe est au-dessus de la tangente. La maîtrise de cette démonstration permet de mieux comprendre les concepts et d'être capable de la reproduire sur une feuille blanche.

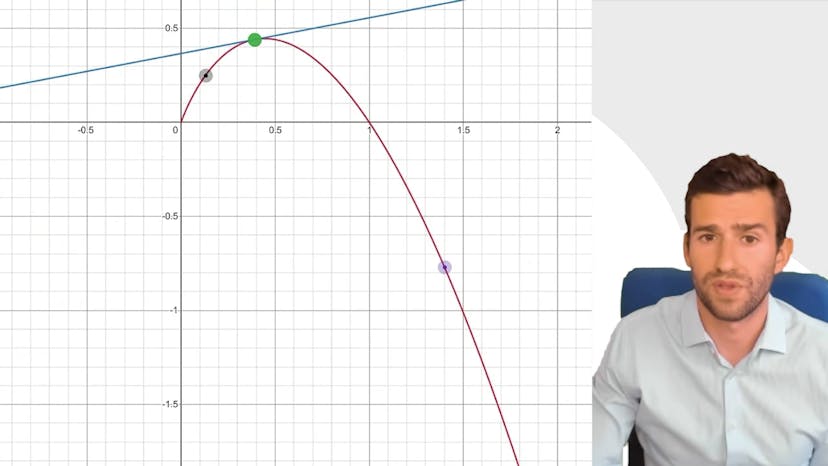
Convexité et f''

Dans ce cours, nous étudions la convexité d'une fonction, ce qui permet de déterminer certaines propriétés intéressantes, notamment la position de la tangente par rapport à la courbe. Dans le premier exemple, nous examinons la fonction f(x) = (1/3)x³ - (3/2)x² + 2x + 1. Nous dérivons cette fonction deux fois et obtenons la dérivée seconde f''(x) = 2x - 3. En analysant le signe de cette dérivée, nous concluons que f est concave pour x < 3/2 et convexe pour x > 3/2. Pour le deuxième exemple, nous étudions la fonction f(x) = 3x - 3x√x. Comme la fonction n'est pas définie pour x < 0 et n'est pas dérivable en 0, nous étudions sa convexité sur l'ensemble des réels positifs. En dérivant f deux fois, nous obtenons f''(x) = -9/(4√x). Comme cette dérivée est toujours négative, nous concluons que f est concave sur tout son ensemble de définition. La concavité d'une courbe signifie que la tangente est toujours au-dessus de la courbe. Il n'y a qu'un seul point de séquence entre la tangente et la courbe. De plus, la courbe est toujours au-dessus des cordes définies par deux points de la courbe. En utilisant la concavité et la convexité, il est possible de déterminer la position relative d'une tangente par rapport à une courbe. Une fonction concave sera en dessous de sa tangente, tandis qu'une fonction convexe aura sa tangente en dessous de la courbe. Cela résume les principaux concepts abordés dans ce cours sur la convexité des fonctions.

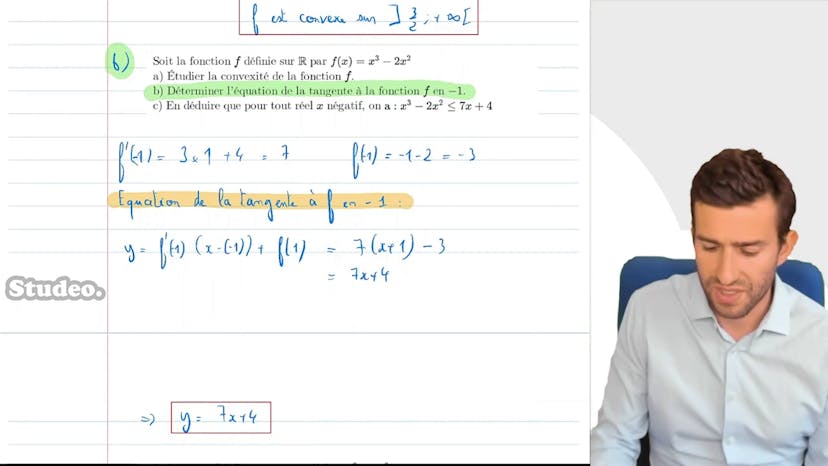
Convexité et Inégalités

Dans ce cours, nous allons étudier la convexité d'une fonction et utiliser cette information pour résoudre des inéquations. Nous commençons par prendre la fonction f(x) = x^3 - 2x^2 et nous calculons ses dérivées f'(x) = 3x^2 - 4x et f''(x) = 6x - 4. Nous étudions le signe de f''(x) pour déterminer la concavité et la convexité de f(x). En résolvant 6x - 4 > 0, nous trouvons que x > 3/2 et en résolvant 6x - 4 < 0, nous trouvons que x < 3/2. Ainsi, nous concluons que f(x) est concave sur l'intervalle (-∞, 3/2) et convexe sur l'intervalle (3/2, +∞). Ensuite, on nous demande de calculer l'équation de la tangente à f(x) en x = -1. En utilisant les formules appropriées, nous obtenons l'équation de la tangente y = 7x + 4. Nous utilisons cette information pour déduire que pour tout x négatif, x^3 - 2x^2 < 7x + 4. Cette inégalité signifie géométriquement que la courbe de f est en dessous de sa tangente, ce qui est le cas lorsque la fonction est concave. Comme nous avons prouvé précédemment que f(x) est concave sur l'intervalle (-∞, 3/2), nous pouvons conclure que l'inégalité est vérifiée dans cet intervalle. Nous illustrons cette propriété en traçant la courbe et la tangente correspondante. Enfin, nous rappelons l'importance de la convexité dans la résolution des inéquations, car sans cette connaissance, l'équation serait plus difficile à résoudre.

Points d'Inflexion

Ce cours est une transcription d'une vidéo qui explique une méthode pour étudier la convexité d'une fonction et trouver ses points d'inflexion. En utilisant la fonction f2x comme exemple, l'orateur explique comment dériver cette fonction deux fois pour déterminer ses variations. Il souligne que le signe de l'exponentielle est toujours positif, et le seul élément important pour déterminer le signe de la dérivée est le terme "-x + 1". Il en déduit un tableau de variations de la fonction f, montrant qu'elle est croissante puis décroissante avec un maximum atteint à 1. Les limites de la fonction sont également calculées pour montrer que la limite en moins l'infini est moins l'infini et la limite en plus l'infini est 0. Ensuite, l'orateur calcule la deuxième dérivée de f et trouve que c'est égal à 7 fois (x-2) fois e^(-x). Il note que l'exponentielle est toujours positive et donc, le signe de la dérivée dépend du signe de (x-2), ce qui est positif pour x>2 et négatif pour x<2. Il conclut que le point x=2 est un point d'inflexion et utilise la formule f(2) pour trouver les coordonnées de ce point. Il explique également que visuellement, un point d'inflexion se distingue par un changement de pente avant et après le point. Enfin, il fait le lien avec les points d'inflexion souvent observés dans des domaines tels que la physique, comme dans le cas d'une courbe de titrage. Cette méthode sur la convexité et les points d'inflexion est la dernière thématique traitée dans le cours. Des questions supplémentaires peuvent être consultées dans la FAQ.

Convexité étude COMPLETE

Aucun résumé n'est disponible pour cette vidéo

Fonctions cubes et convexité

Dans ce cours, nous étudions un exercice qui présente plusieurs paramètres (A, B, C, D) et cherche à montrer un résultat général sur les fonctions x³. Cet exercice est intéressant car il essaie de généraliser des résultats intuitifs concernant les fonctions x³. Nous commençons par analyser la convexité de la fonction f en fonction des valeurs de A. Pour cela, nous calculons la dérivée seconde, f''(x), et la dérivée première, f'(x). Nous remarquons que le signe de f''(x) dépend de la valeur de A. Si A est positif, la fonction est d'abord concave puis convexe. Si A est négatif, la fonction est d'abord convexe puis concave. Nous concluons donc que lorsque A est positif, la fonction f est convexe si et seulement si x > -2B/3A. Lorsque A est négatif, la fonction f est convexe si et seulement si x < -2B/3A. Il est important de faire attention à ne pas confondre ces deux cas. Nous poursuivons l'étude en montrant quels sont les points d'inflexion de la fonction f. Un point d'inflexion est un point où la courbe change de convexité. Nous démontrons que quel que soit le signe de A, la courbe admet un point d'inflexion en abscisse -6B/3A. Enfin, nous appliquons ces résultats à un exemple concret qui nous montre qu'un point donné appartient à la courbe de la fonction f. Nous utilisons les résultats précédents pour montrer que ce point est bien un point d'inflexion de la courbe. En conclusion, cet exercice nous permet de mieux comprendre les propriétés de convexité et de concavité des fonctions x³ en fonction des valeurs de A. Il est important de bien distinguer les différents cas et de structurer notre raisonnement pour éviter les erreurs.

Déf fondamentale

Dans ce cours, nous abordons le concept de logarithme et ses propriétés. Le logarithme naturel, noté ln, est une fonction définie sur les nombres réels strictement positifs. Il associe à tout nombre réel positif x, l'unique solution de l'équation E2y = x pour un y donné. Par exemple, si nous avons E2y = 2, nous pouvons utiliser le logarithme de 2 (log 2) pour représenter la solution. Le logarithme inverse de l'exponentielle est également une propriété importante. Mathématiquement, pour tout x positif, l'exponentielle de log x est égale à x. De même, pour tout x appartenant à R, le logarithme de l'exponentielle de x est égal à x. Ces deux fonctions sont donc réciproques l'une de l'autre, tout comme la racine carrée et le carré. Cependant, il est important de noter que le logarithme est uniquement défini pour les x positifs, contrairement à l'exponentielle qui est définie pour tous les réels. Nous avons également mentionné quelques valeurs particulières telles que log 1 = 0, log e = 1 et log(1/e) = -1. Il est crucial de faire attention aux ensembles d'existence pour ces égalités, car ils diffèrent pour le logarithme et l'exponentielle. En résumé, le logarithme est une fonction qui permet de trouver l'unique solution d'une équation exponentielle et possède une relation réciproque avec l'exponentielle. Il est important de prendre en compte les ensembles de définition pour éviter les erreurs.

Simplifier des expressions

Dans ce cours, nous traitons des propriétés et des méthodes pour résoudre des inéquations avec des exponentielles et des logarithmes. Voici un résumé SEO-friendly des différentes équations et inéquations traitées dans la vidéo : 1. Équation : ln(x) = 2 - Composez par l'exponentielle pour obtenir x = e^2. 2. Équation : e^x + 1 = 5 - Composez par le logarithme pour obtenir x + 1 = ln(5). - Résolvez pour x en soustrayant 1 de chaque côté : x = ln(5) - 1. 3. Équation : 3ln(x) - 4 = 8 - Divisez par 3 pour obtenir ln(x) - 4/3 = 8/3. - Composez par l'exponentielle pour obtenir x = e^(4/3). 4. Inéquation : ln(6x - 1) > 2 - Vérifiez que l'expression à l'intérieur du logarithme est strictement positif (6x - 1 > 0). - Composez par l'exponentielle pour obtenir 6x - 1 > e^2. - Résolvez pour x en trouvant que x > (e^2 + 1)/6. 5. Inéquation : e^x + 5 > 4e^x - Rassemblez tous les termes exponentiels ensemble pour obtenir e^x < 5/3. - Composez par le logarithme pour obtenir x < ln(5/3). 6. Équation : ln(x - 3) + ln(9 - x) = 0 - Rassemblez les termes logarithmiques pour obtenir ln((x - 3)(9 - x)) = 0. - Composez par l'exponentielle pour obtenir (x - 3)(9 - x) = 1. - Résolvez l'équation quadratique pour trouver les solutions x1 = 6 + racine(8) et x2 = 6 - racine(8). - Vérifiez que ces solutions sont dans l'intervalle valide (3, 9). 7. Inéquation : ln(3 - x) - ln(x + 1) < 0 - Vérifiez les valeurs possibles pour x (3 - x > 0 et x + 1 > 0), ce qui donne -1 < x < 3. - Rassemblez les termes logarithmiques en utilisant la propriété ln(a) - ln(b) = ln(a/b) pour obtenir ln((3 - x)/(x + 1)) < 0. - Composez par l'exponentielle pour obtenir (3 - x)/(x + 1) < 1. - Multipliez par (x + 1) sans changer le sens de l'inégalité (car (x + 1) > 0), ce qui donne 3 - x < x + 1. - Résolvez l'inéquation pour trouver x > 2. Il est important de toujours considérer l'ensemble de définition de l'équation ou de l'inéquation traitée afin d'exclure les solutions invalides. Il est également essentiel de faire attention aux signes lors de la manipulation d'équations et d'inéquations. Le regroupement des termes logarithmiques et exponentiels est une méthode utile pour résoudre ces types de problèmes.

Équations Inéquations

Ce cours sur les inéquations avec logarithmes explique comment résoudre une équation donnée en isolant le terme en ln. Après avoir vérifié l'ensemble de définition de l'inéquation, l'objectif est de composer par l'exponentiel pour isoler le ln. Ensuite, on résout l'équation simple obtenue et on prend en compte l'ensemble de définition initial pour déterminer l'intervalle solution. Attention à bien faire correspondre les ensembles de définition pour éviter les erreurs. Cette méthode consiste donc à isoler le terme en logarithme, composer par l'exponentiel et prendre l'intersection de la solution finale avec l'ensemble de définition initial.