 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths Spé
Analyse
Terminale

Introduction
Ce sous-chapitre sur les intégrales, les applications et calculs aborde l'utilisation de méthodes comme l'intégration par partie pour calculer des primitives plus complexes qui ne figurent pas dans les tables classiques. Il permet également de calculer des r sous les courbes (r entre des courbes) en utilisant le lien entre r et primitive établi dans le sous-chapitre précédent. Il aborde également la définition de la valeur moyenne d'une fonction, avec des méthodes associées. En résumé, ce sous-chapitre permet de calculer des r sous une courbe, entre deux courbes, de calculer la valeur moyenne d'une fonction et de faire du calcul intégral par intégration par partie, notamment à travers des exercices difficiles.
Maths Spé
Analyse
Terminale

Intégration par Parties
L'intégration par partie est une formule importante en mathématiques pour calculer des primitives ou résoudre des équations différentielles. La formule en gros dit que l'intégrale de uv' est égale à la primitive de u x v entre a et b moins l'intégrale entre a et b de u' x v. Elle est utile pour des intégrales compliquées où il n'est pas possible de trouver une primitive facilement. L'astuce consiste à interpréter les termes du produit comme u et v', puis à appliquer la formule pour simplifier l'inté
Maths Spé
Analyse
Terminale

Aire entre 2 courbes
Dans cette vidéo, on apprend comment calculer l'air entre deux courbes en utilisant le théorème suivant : Soit f et g, deux fonctions continues sur un intervalle i, tel que f2x est toujours plus petite que g2x. L'air exprimé en unité d'air du domaine, compris entre x égal a et x égal b, donc les bords de l'intervalle, et la courbe de f et la courbe de g, vaut l'intégrale entre a et b de g2x moins f2x. Pour illustrer cette propriété, l'auteur utilise deux fonctions f en rouge et g en bleu et montre que l'air entre les deux courbes est égal à l'intégrale de f moins g lorsque f est au-dessus de g et à l'intégrale de g moins f lorsque g est au-dessus de f.
Maths Spé
Analyse
Terminale
Valeur Moyenne
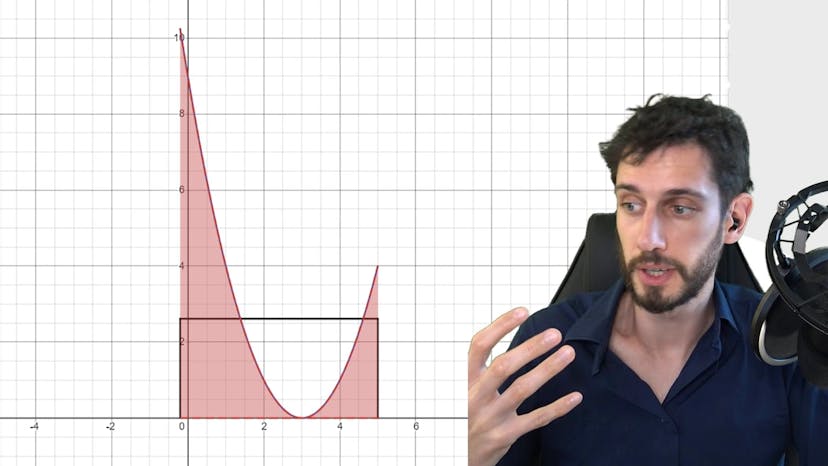
La valeur moyenne d'une fonction est définie comme le nombre mu égal à 1 sur b moins a fois l'intégrale entre a et b de f, où f est une fonction continue. On peut voir la valeur moyenne comme une moyenne arithmétique des rectangles infiniment fins entre a et b. Elle peut également être comprise géométriquement comme la valeur constante telle que l'air sous la courbe de la fonction constante soit égale à l'air sous la courbe de f. La valeur moyenne est la hauteur du rectangle parfait qui a la même aire que l'aire sous la courbe de f. Elle est utile pour résoudre des exercices de méthodes. Si vous avez des questions, la FAQ est ouverte.
Maths Spé
Analyse
Terminale

Intégration par Parties : Calcul
La méthode d'intégration par partie est utilisée pour calculer des intégrales en décomposant une fonction en deux parties et en utilisant les propriétés de la dérivée du produit. Voici les étapes principales pour appliquer cette méthode :
1. La formule de l'intégration par partie est donnée par l'intégrale de U'V moins l'intégrale de UV'. Cette formule est basée sur la dérivée du produit, UV' = U'V + UV.
2. Il est important de choisir judicieusement les deux parties U' et V afin d'avoir un résultat simplifié. Trois points sont à considérer :
a. Il doit y avoir un produit dans l'intégrale pour pouvoir appliquer la méthode.
b. Au moins l'une des deux fonctions doit avoir une primitive facile à calculer.
c. La dérivée de l'autre fonction doit simplifier le calcul.
3. Pour appliquer la méthode, on calcule U'V et UV' en utilisant les choix de U' et V. On intègre U'V et on trouve la primitive de UV'.
4. On simplifie l'expression obtenue en remplaçant les termes entre crochets par leur valeur. On continue ensuite avec le calcul et on obtient le résultat final.
Dans cet exemple spécifique, l'intégrale à calculer est l'intégrale de X ln(X) entre 1 et E. On choisit U' = X et V = ln(X) et on calcule U'V et UV'.
En utilisant la formule de l'intégration par partie, on obtient une expression simplifiée : X²/2-ln(X)/2.
En évaluant cette expression entre 1 et E, on obtient le résultat final : E²/2-1/4.
Il est important de noter que l'ordre de dérivation et d'intégration peut être inversé dans certains cas, mais il est préférable de choisir la méthode qui facilite le calcul. Pour éviter les erreurs, il est recommandé d'écrire U', U, V et V' clairement afin de suivre les étapes plus facilement.
Maths Spé
Analyse
Terminale

Aire sous une Courbe : Calcul
Dans ce cours, nous abordons le calcul d'erreurs sous une courbe à l'aide d'intégrales. Deux exemples sont présentés pour illustrer cette méthode.
Le premier exemple concerne l'erreur entre la courbe CF, définie par l'équation f2x=x²-4, et l'axe d'étape 6, entre les valeurs x=-2 et x=2. Pour calculer cette erreur, nous devons trouver la primitive de la fonction x²-4 à l'intérieur de l'intégrale. En trouvant la primitive, qui est un tiers de x au cube moins 4x, nous appliquons le théorème fondamental pour obtenir l'erreur. Nous effectuons les calculs en faisant attention aux signes négatifs. Dans ce cas, l'erreur est égale à -32/3.
Le deuxième exemple concerne l'erreur entre la courbe et l'axe des abscisses entre les valeurs x=-5 et x=1. Encore une fois, nous devons trouver la primitive de la fonction x²-4 et calculer l'intégrale entre les bornes. En simplifiant les calculs, nous trouvons une erreur de 18. Visuellement, la courbe présente une partie positive et une partie négative, mais la somme des deux nous donne une erreur positive.
Il est important de noter que la variable d'intégration est spécifiée dans l'équation et ne peut pas être modifiée. Dans le premier exemple, la variable est x, tandis que dans le deuxième exemple, elle est t.
En résumé, ce cours explique comment calculer les erreurs sous une courbe à l'aide d'intégrales. Deux exemples sont présentés, montrant les calculs et les erreurs obtenues.
Maths Spé
Analyse
Terminale
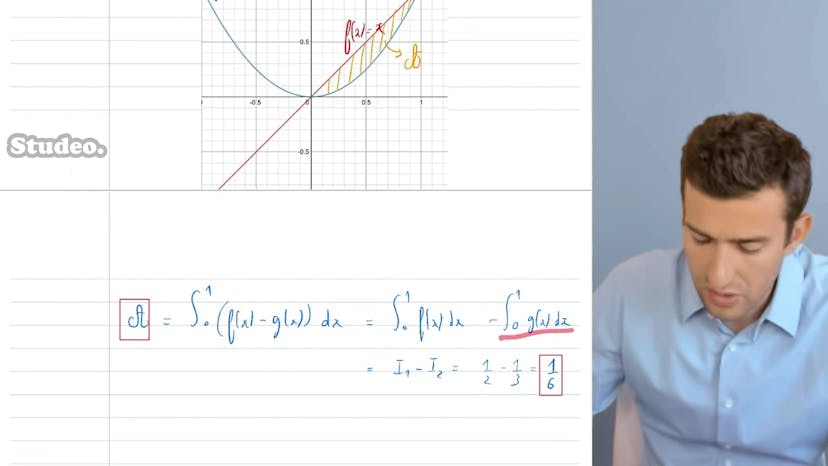
Aire entre 2 Courbes
Dans cette vidéo, nous apprenons comment calculer l'R entre deux courbes, à savoir les fonctions f2x = x et g2x = x², sur l'intervalle [0, 1]. Pour cela, il est nécessaire de trouver les primitives des deux fonctions. Pour f2x, la primitive est f2x = x²/2, tandis que pour g2x = x², la primitive est g2x = x³/3.
En utilisant le théorème fondamental, nous pouvons représenter visuellement les deux fonctions f et g. L'R sous la courbe est la zone qui est encadrée et qui sera appelée "1". Pour faciliter le calcul, nous choisissons de prendre l'R plutôt positif en prenant la différence entre la fonction supérieure et la fonction inférieure sur l'intervalle. Dans ce cas précis, f est toujours supérieure à g sur l'intervalle [0, 1].
En calculant l'intégrale de f2x - g2x, nous obtiendrons la valeur de notre R entre 0 et 1. En utilisant les propriétés de l'intégrale, nous pouvons écrire cette différence comme l'intégrale de f moins l'intégrale de g sur l'intervalle [0, 1].
Après avoir effectué les calculs nécessaires, nous trouvons que l'intégrale de f2x de 0 à 1 est égale à 1/2 et l'intégrale de g2x de 0 à 1 est égale à 1/3. Par conséquent, la différence entre ces deux valeurs est de 1/6. Ainsi, l'R entre les deux courbes sur l'intervalle [0, 1] est de 1/6. C'est ainsi que l'on calcule l'R entre deux courbes.
Maths Spé
Analyse
Terminale

Calcul Valeur Moyenne
La valeur moyenne d'une fonction f sur un intervalle est donnée par l'intégrale de la fonction sur l'intervalle, divisée par la largeur de l'intervalle. On peut déterminer la primitive de la fonction f en utilisant le théorème fondamental de l'intégration. Une fois la primitive trouvée, on peut calculer la valeur moyenne en substituant les bornes de l'intervalle dans la primitive et en effectuant les calculs nécessaires.
Dans l'exemple présenté, nous avons deux fonctions f et g avec des intervalles légèrement différents. Pour calculer la valeur moyenne de f, nous posons h(x) = x² + 3 et utilisons le théorème fondamental pour trouver une primitive de h, qui est H(x) = (1/3)x³ + 3x. En utilisant la définition de la valeur moyenne, nous divisons l'intégrale de f sur l'intervalle par la largeur de l'intervalle pour obtenir la valeur moyenne 13/3.
Pour calculer la valeur moyenne de g, nous avons la fonction g(x) = x / (x² - 3) et la largeur de l'intervalle est 4 - e. En cherchant une primitive de g, nous remarquons qu'elle ressemble à un quotient de dérivées. Nous ajustons légèrement le quotient pour obtenir la forme u' / u, avec u = x² - 3. La primitive de g est alors k(x) = (1/2)ln|x² - 3|. En simplifiant l'expression et en substituant les bornes de l'intervalle, nous obtenons la valeur moyenne de g.
Il suffit d'appliquer la définition de la valeur moyenne et de faire les calculs d'intégration pour obtenir la valeur moyenne d'une fonction sur un intervalle donné.
Maths Spé
Analyse
Terminale

Suite d'Intégrales
Dans ce cours, on étudie une suite d'intégrales et on cherche à trouver sa convergence. On nous pose une suite de fonctions fn de t qui vaut 1 sur 1 plus t à la puissance n et in qui va être l'intégrale de 0 à 1 de cette fonction fn. On guide l'exercice en essayant d'encadrer cette fonction entre 1 et 1 moins t à la puissance n. La première méthode consiste à construire des inégalités. On obtient le premier bout de l'inégalité en suivant ce raisonnement : 1,5 est compris entre 1 sur 1 plus t à la puissance n qui est plus petit que 1. Pour le deuxième, on multiplie par moins 1 et on essaie de sommer avec l'autre inégalité. Quand cela ne marche pas, on fait la méthode instinctive en faisant la différence.Ensuite, on calcule l'intégrale en utilisant la linéarité de l'intégrale et on trouve l'encadrement de la suite.Finalement, on utilise le théorème d'encadrement pour montrer que la suite converge et donner sa limite qui est 1.
Maths SM&SP
Analyse
2BAC SM Maroc

Introduction
Dans ce cours, nous allons utiliser les intégrales pour calculer des primitives plus complexes à l'aide de la méthode d'intégration par partie. Nous pourrons calculer des aires entre des courbes en utilisant le lien entre les intégrales et les primitives. Nous étudierons également la définition de la valeur moyenne d'une fonction et verrons quelques méthodes associées. En résumé, nous aborderons le calcul d'aires sous une courbe, entre deux courbes, la valeur moyenne d'une fonction et l'intégration par partie. Nous nous concentrerons particulièrement sur des exercices plus difficiles pour explorer les limites de ces méthodes. N'hésitez pas à consulter la FAQ si vous avez des questions ou des doutes. À bientôt pour la prochaine vidéo.
Maths SM&SP
Analyse
2BAC SM Maroc

Intégration par Parties
Bienvenue dans cette vidéo sur l'intégration par parties. Je vais vous expliquer en détail cette méthode car elle est très importante dans le chapitre et revient souvent dans les exercices. Dans un premier temps, je vais vous montrer d'où vient cette formule et vous la démontrer. Puis je vous montrerai comment l'appliquer concrètement.
Le théorème de l'intégration par parties est formulé comme c
Maths SM&SP
Analyse
2BAC SM Maroc

Aire entre 2 courbes
Dans cette vidéo, on explique comment calculer l'aire entre deux courbes, en utilisant le théorème suivant : Soit f et g deux fonctions continues sur un intervalle i, telles que f(x) soit toujours plus petite que g(x). Alors, l'aire exprimée en unité d'aire, du domaine compris entre les points x=a et x=b, ainsi que les courbes f et g, est égale à l'intégrale de g(x) - f(x) entre a et b.
L'illustration montre deux fonctions, f en rouge et g en bleu. En utilisant le théorème, on peut calculer l'aire entre les courbes lorsque f est au-dessus de g. Par exemple, pour l'intervalle entre 0 et 2, l'aire serait équivalente à l'intégrale de f(x) - g(x).
Après le point de croisement, il faut faire attention car les comportements des fonctions changent. Dans ce cas, l'aire entre les courbes serait égale à l'intégrale de g(x) - f(x) entre ce point et 5.
L'objectif de cette vidéo était de donner une illustration visuelle de cette propriété. Si vous avez des questions, vous pouvez vous référer à la FAQ.
Maths SM&SP
Analyse
2BAC SM Maroc

Valeur Moyenne
La valeur moyenne d'une fonction f est définie comme étant le nombre µ égale à 1 sur b-a fois l'intégrale entre a et b de f, où a et b sont les bornes de l'intervalle.
Pour comprendre cette notion, on peut faire un parallèle avec la moyenne arithmétique. L'intégrale entre a et b est en réalité une somme infinie de rectangles infiniment fins. Puis, on divise cette somme par le nombre total de rectangles, ce qui correspond à la taille totale du groupe.
On peut également visualiser la valeur moyenne de manière géométrique. On peut considérer µ comme une valeur constante telle que l'aire sous la courbe de la fonction constante est égale à µ fois la largeur du rectangle égale à l'aire sous la courbe de f.
Pour illustrer cela, on peut tracer un graphe où la valeur moyenne correspond à l'endroit où l'aire du rectangle est égale à l'aire sous la courbe de f. Si le rectangle est trop bas ou trop haut, les aires ne seront pas égales. Il y a donc un moment où le rectangle parfait est trouvé, et c'est à ce moment que la valeur moyenne est obtenue.
La compréhension de la valeur moyenne sera approfondie dans les exercices et les vidéos de méthodes à venir. Si vous avez des questions théoriques, vous pouvez les poser dans la FAQ. À la prochaine vidéo !
Maths SM&SP
Analyse
2BAC SM Maroc

Intégration par Parties : Calcul
L'intégration par partie est une méthode utilisée en calcul pour résoudre des intégrales. Cette méthode est basée sur l'utilisation de la formule suivante : l'intégrale de U'V est égale à UV moins l'intégrale de UV'.
Pour bien comprendre cette formule, il est important de se rappeler d'où elle vient. Elle est dérivée du produit de dérivées, c'est-à-dire U'V plus UV'. En calculant l'intégrale de cette somme, on obtient la formule d'IPP.
Pour utiliser cette méthode, il faut choisir judicieusement les fonctions U et V. Il y a trois critères à prendre en compte : il faut avoir un produit dans l'intégrale, au moins l'un des deux facteurs doit avoir une primitive facilement calculable, et la dérivée de l'autre fonction doit faciliter le calcul. L'objectif de l'intégration par partie est d'échanger une intégrale complexe contre une autre plus simple.
Pour illustrer cette méthode, prenons l'exemple d'une intégrale à calculer : l'intégrale de X ln(X) entre 1 et E. Dans ce cas, on a le produit X ln(X) et les fonctions U = X et V' = ln(X). En calculant les primitives, on trouve que la primitive de U est X²/2 et la primitive de V est X ln(X) - X. Ainsi, on peut appliquer l'intégration par partie en remplaçant l'intégrale initiale par X²/2 ln(X) entre 1 et E moins l'intégrale de X²/2 (1/X) entre 1 et E. En simplifiant les termes, on obtient X/2 et il est plus facile de calculer cette intégrale. Finalement, on trouve que l'intégrale initiale est égale à E² + 1/4.
Il est important de noter que l'intégration par partie peut parfois être appliquée dans les deux sens, mais il est préférable de choisir la méthode qui facilite le calcul. Il est également conseillé de noter les fonctions U', U, V et V' sur une feuille de brouillon afin de ne pas se tromper lors des étapes de calcul.
Cet exemple illustre comment appliquer l'intégration par partie pour résoudre une intégrale. N'hésitez pas à poser des questions supplémentaires dans la FAQ.
Maths SM&SP
Analyse
2BAC SM Maroc

Aire sous une Courbe : Calcul
Dans ce cours, nous abordons le calcul des erreurs sous une courbe à l'aide d'intégrales. Nous allons prendre deux exemples pour calculer ces erreurs, ce qui revient à calculer des intégrales.
Le premier exemple concerne l'erreur entre la courbe CF dont l'équation est f2x = x²-4, et l'axe d'étape 6 entre les droites d'équation x = -2 et x = 2. Mathématiquement, cela se traduit par l'intégrale de x²-4dx entre -2 et 2. Nous devons trouver la primitive de la fonction à l'intérieur de l'intégrale. Pour cela, nous posons f2x = x²-4, une fonction polynomiale pour laquelle nous trouvons facilement une primitive. Nous prenons la primitive de chaque terme, soit un tiers de x au cube moins 4x. Ensuite, nous utilisons le théorème fondamental pour trouver l'erreur, qui est égale à un tiers de x au cube moins 4x entre -2 et 2. Après les calculs, nous obtenons -32/3 pour l'erreur.
Le deuxième exemple concerne l'erreur entre la courbe et l'axe des abscisses entre les droites d'équation x = -5 et x = 1. Nous devons calculer l'intégrale de x²-4 entre -5 et 1. Encore une fois, la primitive de la fonction reste la même, seules les bornes changent. Après simplification, nous obtenons 18 pour l'erreur.
Il est important de noter que la variable d'intégration est x, ce qui signifie qu'elle ne peut pas être utilisée ailleurs dans la fonction. Dans le premier exemple, l'erreur est négative car la partie sous la courbe est située en dessous de l'axe des abscisses. Dans le deuxième exemple, la somme des parties positives et négatives de la courbe nous donne une erreur positive de 18.
Pour plus d'informations, vous pouvez consulter la FAQ.
Maths SM&SP
Analyse
2BAC SM Maroc
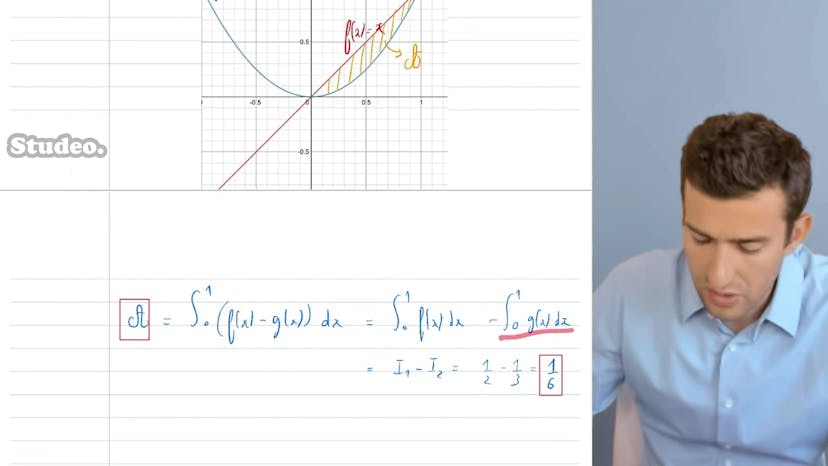
Aire entre 2 Courbes
Dans ce cours, nous allons apprendre à calculer "R" entre deux courbes. Les courbes données sont f(x) = x et g(x) = x², et nous voulons calculer "R" entre elles, dans l'intervalle de x = 0 à x = 1. Pour effectuer ce calcul, nous devons tout d'abord trouver les primitives des deux fonctions f et g. Les primitives de f(x) = x et g(x) = x² sont respectivement F(x) = x²/2 et G(x) = x³/3. Ensuite, nous utilisons le théorème fondamental du calcul intégral.
Visuellement, l'R se situe sous la courbe entre f et g. Dans notre cas, nous voulons prendre une valeur positive pour l'R. Donc, nous calculons la différence entre la fonction qui est supérieure à l'autre sur l'intervalle donné. Dans notre cas, f est toujours supérieure à g pour tous les x de 0 à 1. Donc, nous calculons l'intégrale de f(x) - g(x) de 0 à 1 pour obtenir la valeur de notre R.
En appliquant les propriétés de l'intégrale, nous obtenons l'intégrale de 0 à 1 de f(x) - l'intégrale de 0 à 1 de g(x). Nous avons déjà calculé ces intégrales et les avons appelées I1 et I2. En utilisant le théorème fondamental du calcul intégral, nous trouvons que I1 = 1/2 et I2 = 1/3. Donc, la différence entre 1/2 et 1/3 est égale à 1/6. Donc, l'R entre les deux courbes, dans l'intervalle de 0 à 1, est égal à 1/6. C'est ainsi que l'on calcule l'R entre deux courbes.
Maths SM&SP
Analyse
2BAC SM Maroc

Calcul Valeur Moyenne
Dans ce cours, nous abordons le calcul de la valeur moyenne d'une fonction. Nous avons deux exemples avec des fonctions différentes et des intervalles légèrement différents.
La valeur moyenne est l'intégrale de la fonction sur l'intervalle, divisée par la largeur de cet intervalle. Dans notre exemple, la largeur de l'intervalle est de 4 (2 - (-2)).
Pour la première fonction f, nous trouvons une primitive h en utilisant le théorème fondamental. En faisant les calculs, nous obtenons 13/3 comme résultat pour l'intégrale de f sur l'intervalle.
Pour la deuxième fonction g, nous devons d'abord trouver une primitive de g en utilisant la méthode du quotient. Nous remarquons que nous avons un quotient avec un coefficient manquant, mais nous le faisons apparaître en multipliant par 1/2 * 2. La primitive de g est alors 1/2 ln(|x² - 3|).
En appliquant la définition de la valeur moyenne à g, nous trouvons l'intégrale de g sur l'intervalle et effectuons les calculs nécessaires. Nous obtenons une expression avec un ln de (16 - 3), que nous ne pouvons pas simplifier davantage.
En résumé, le calcul de la valeur moyenne d'une fonction consiste simplement à appliquer la définition et à effectuer un calcul intégral.
Maths SM&SP
Analyse
2BAC SM Maroc

Suite d'Intégrales
La méthode utilisée pour étudier la convergence d'une suite d'intégrales est présentée dans ce cours. La suite de fonctions fn est définie comme 1/(1+t)^n. L'objectif est de trouver la convergence de cette suite.
La première méthode consiste à construire des inégalités. En utilisant les propriétés des puissances et des fonctions inverses, on montre que la fonction est encadrée entre 1 et 1-(1+t)^n. Cependant, cette méthode ne fonctionne pas pour la deuxième inégalité.
Une autre approche consiste à prendre la différence entre les deux expressions et à montrer qu'elle est positive. En simplifiant l'expression, on obtient une forme du type a^2 - b^2, ce qui permet de conclure que 1-(1+t)^n est inférieur à 1/(1+t)^n.
Ensuite, on calcule l'intégrale de 1- t^n de 0 à 1 et on trouve (n/(n+1)). On utilise ensuite la linéarité de l'intégrale pour encadrer cette intégrale.
Finalement, on montre que la suite des intégrales converge vers 1 à l'aide du théorème d'encadrement. On utilise les informations précédentes pour conclure que la suite converge et donner sa limite.


