Cours de Réactions chimiques en Ligne par les Meilleurs Professeurs - Réactions chimiques

Energie d'activation

Dans cette vidéo, Matisse de Studio explique comment calculer l'énergie d'activation d'une réaction chimique en utilisant la formule d'Arenus. Il commence par expliquer que la vitesse de réaction double lorsque la température passe de 300 Kelvin à 400 Kelvin. Il fait l'hypothèse que la constante de vitesse double également. En utilisant la loi d'Arenus, il montre que la constante de vitesse est égale à A multiplié par l'exponentielle de moins EA/RT, où EA représente l'énergie d'activation, A est un facteur pré-exponentiel, R est la constante des gaz parfaits et T est la température de réaction. Sachant que la constante de vitesse double, il nomme K1 et K2 les constantes de vitesse pour les réactions réalisées à 300 Kelvin et 400 Kelvin respectivement. En utilisant la loi d'Arenus, il établit l'équation K2 = 2K1. En simplifiant l'équation, il isole l'énergie d'activation EA et trouve que EA est égal à R ln 2 divisé par 1/T1 - 1/T2. Il conclut que l'énergie d'activation de la réaction est de 6,9 kJ/mol. Il conseille de prendre son temps pour comprendre l'énoncé, donner des noms aux variables et utiliser la formule d'Arenus pour résoudre l'exercice.

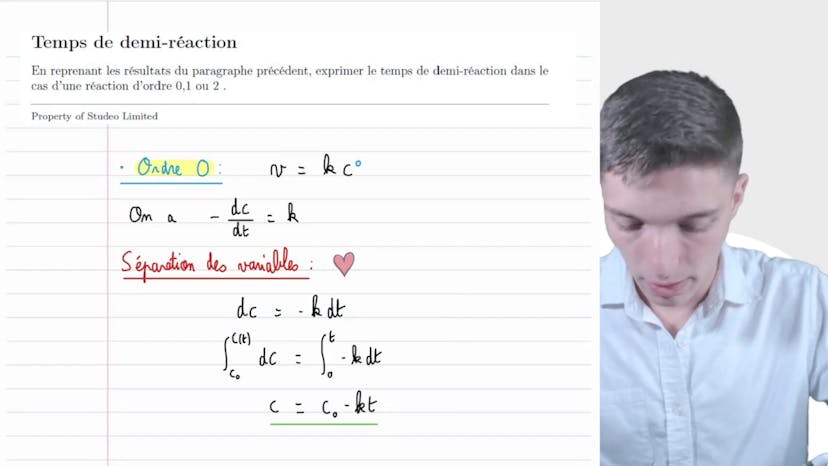
Temps de demi réaction

Dans cette vidéo, Mathis de Studio traite des différents temps de demi-réaction pour les réactions d'ordre 0, 1 et 2. Il explique que ces notions sont essentielles à connaître pour les examens et les exercices. Pour les réactions d'ordre 0, la vitesse de réaction peut être exprimée comme V = k * [A]^0, où [A]^0 représente la concentration d'une espèce qui disparaît. En résolvant cette équation, on obtient que la concentration en fonction du temps est donnée par c = c0 - kt, où c0 est la concentration initiale et k est la constante de vitesse. Le temps de demi-réaction peut alors être calculé en résolvant c = c0/2, ce qui donne t1/2 = c0/(2k). Pour les réactions d'ordre 1, la vitesse de réaction peut être exprimée comme V = k * [A]^1, où [A]^1 représente la concentration d'une espèce qui disparaît avec un coefficient stoichiométrique de 1. En suivant les étapes similaires, on obtient que la concentration en fonction du temps est donnée par c = c0 * e^(-kt). Le temps de demi-réaction peut alors être calculé en résolvant c = c0/2, ce qui donne t1/2 = ln(2)/k. Enfin, pour les réactions d'ordre 2, la vitesse de réaction peut être exprimée comme V = k * [A]^2, où [A]^2 représente la concentration d'une espèce qui disparaît avec un coefficient stoichiométrique de 2. En suivant les étapes similaires, on obtient que la concentration en fonction du temps est donnée par c = c0/(1 + c0kt). Le temps de demi-réaction peut alors être calculé en résolvant c = c0/2, ce qui donne t1/2 = 1/(c0k). En résumé, cette vidéo explique comment déterminer les temps de demi-réaction pour les réactions d'ordre 0, 1 et 2, en utilisant les équations d'évolution de la concentration en fonction du temps.

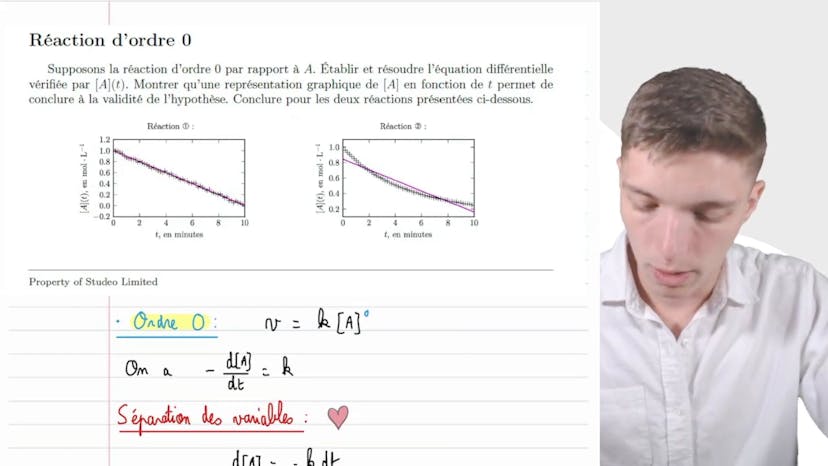
Réaction d'odre 0

Dans cette vidéo, nous vérifions si une réaction chimique est d'ordre zéro ou non. Pour cela, nous faisons une hypothèse sur l'ordre de réaction et examinons les conséquences de cette hypothèse sur la cinétique de la réaction. Nous devons établir et résoudre l'équation différentielle qui décrit la concentration du réactif en fonction du temps. En analysant la représentation graphique de la concentration en fonction du temps, nous pouvons conclure si notre hypothèse est valide ou non. Dans cet exercice, nous obtenons deux courbes différentes pour les deux réactions étudiées. La première courbe est une droite qui passe par tous les points, indiquant une cinétique d'ordre zéro, tandis que la deuxième courbe est une courbe polynomial ou convexe, indiquant une cinétique différente de l'ordre zéro. En résolvant l'équation différentielle, nous obtenons une fonction affine décroissante pour la première réaction, confirmant notre hypothèse. En conclusion, la première réaction est d'ordre zéro par rapport au réactif A, tandis que la deuxième réaction n'est pas d'ordre zéro. Cette analyse nous permet de déterminer l'ordre de réaction à partir de la courbe d'évolution de la concentration. C'est un exemple puissant de la puissance des calculs analytiques et des observations expérimentales en cinétique chimique.

Vitesse de réaction

Dans cette vidéo, Mathis explique le lien entre la vitesse de réaction et la concentration. Il commence par donner une équation bilan pour une réaction chimique donnée. Il construit ensuite un tableau d'avancement de la réaction en termes de concentration. Il déduit ensuite l'expression de l'avancement volumique en fonction de la concentration pour chaque espèce. Ensuite, il montre que la vitesse de réaction est simplement la dérivée de l'avancement volumique par rapport au temps. Il démontre ainsi l'expression de la vitesse de réaction en fonction de la concentration des ions. Il conclut en soulignant l'importance de comprendre ces concepts en chimie.

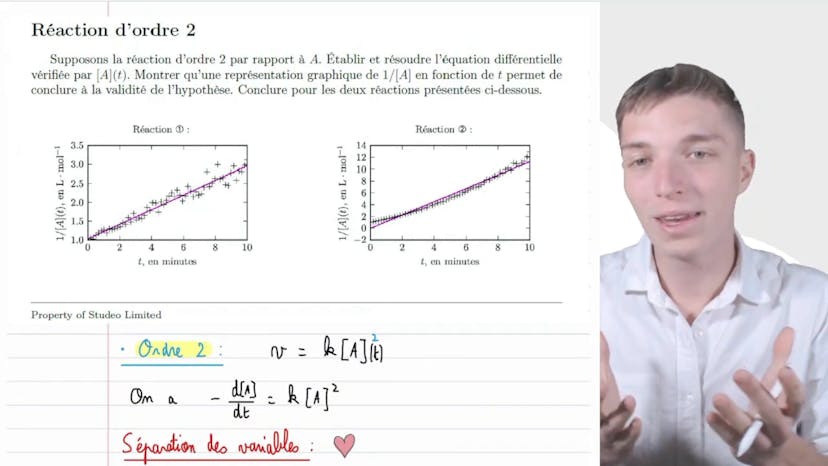
Réaction d'ordre 2

Dans cette vidéo, nous allons vérifier si une réaction est d'ordre 2 ou non. Pour cela, nous supposons que la réaction est d'ordre 2 par rapport au réactif A. Nous devons établir et résoudre l'équation différentielle vérifiée par la concentration de A en fonction du temps. Une représentation graphique de 1/concentration en fonction du temps nous permettra de conclure à la vérité de l'hypothèse pour les deux réactions présentées. Pour la réaction 1, nous observons une droite qui peut être modélisée et qui passe par la plupart des points. Cela est cohérent. Pour l'autre réaction, nous avons un polynôme qui est mal approximé par la régression linéaire. Pour exprimer 1/concentration en fonction du temps, nous utilisons l'équation v=k[A]^2. En effectuant la séparation des variables et en intégrant, nous obtenons la relation 1/concentration à l'instant t = kt + 1/concentration initiale. Cette relation nous dit que la courbe de 1/concentration en fonction du temps est une fonction affine et croissante. Ainsi, la réaction 1 présente une cinétique d'ordre 2 par rapport à A. Ce n'est pas le cas pour la réaction 2. En conclusion, en analysant l'évolution de la concentration en fonction du temps, nous pouvons déterminer l'ordre de la réaction. Cette démarche est puissante et nous permet de comprendre les caractéristiques cinétiques des réactions. Merci d'avoir visionné cette vidéo et à bientôt !

Décomposition de l'éthanal

Dans cette vidéo, nous étudions la décomposition de l'éthanal (CH3CHO) en méthane (CH4) et monoxyde de carbone (CO). Les composés sont tous gazeux. Nous sommes également dans une enceinte fermée et indéformable, avec une pression initiale P0. Nous écrivons l'équation de la réaction et construisons le tableau d'avancement. On constate que la mesure de la pression à l'intérieur de l'enceinte permet de suivre l'avancement de la réaction, car elle dépend directement du nombre de moles des différents composés. On exprime la pression en fonction de l'avancement et des molécules présentes. Ensuite, on montre expérimentalement que la fonction f est proportionnelle à la température T. On utilise la formule de la concentration en éthanal pour une réaction d'ordre 2 et exprimons f en fonction de cette formule. On démontre alors que f est une fonction linéaire du temps, ce qui est compatible avec une réaction d'ordre 2. Nous calculons ensuite le temps de demi-réaction en utilisant les informations disponibles et obtenons l'expression V/(N0*K), typique d'une réaction d'ordre 2. Enfin, nous notons que si le volume est doublé, le temps de demi-réaction sera également deux fois plus important. En conclusion, cet exercice nous montre l'importance d'exprimer les grandeurs en fonction des hypothèses et des formules disponibles. Il permet également de comprendre comment mesurer et suivre l'avancement d'une réaction grâce à une grandeur physique, comme la pression.

Ions iodures et ferriques

Dans cette vidéo, Matisse de Studio explique le processus d'oxydation des ions iodure par les ions fériques. Il présente une équation de bilan : 2Fe3+ + 2I- -> 2Fe2+ + I2. Il réalise deux séries d'expériences à température constante pour déterminer les vitesses initiales en utilisant une méthode appelée "horloge à iode". Pour la première série, la concentration initiale en I- est fixée à 4x10^-3 mol/L, tandis que pour la deuxième série, c'est la concentration initiale en Fe3+ qui est fixée à 1,67x10^-3 mol/L. Ensuite, il propose un modèle mathématique pour exprimer la vitesse initiale de réaction en fonction des concentrations initiales des réactifs. En utilisant une régression linéaire, il détermine les ordres partiels de réaction par rapport à I- (α) et par rapport à Fe3+ (β). Il obtient β = 1 et α = 2. Il utilise également les résultats de la régression linéaire pour déterminer les constantes de vitesse apparentes (K-up et K'). Enfin, il calcule la valeur de la constante de vitesse (K) à partir de K' et de la concentration initiale en Fe3+. En conclusion, Matisse établit la loi de vitesse initiale de la réaction étudiée : V0 = K [I-]^2 [Fe3+]^1, avec K = 4,55 mol-2 L2s-1. Il souligne que ces résultats concernent uniquement la vitesse initiale de réaction.

Loi d'Arrhenius

Dans cette vidéo, Mathis de Studio explique la loi d'Arenius qui concerne la décomposition du pâte à oxyde d'azote N2O5 en dioxyde azote NO2 et en dioxygène à une température de θ supérieure ou égale à 150°C. Il démontre comment écrire l'équation de la réaction en utilisant les nombres stoichiométriques appropriés. Il poursuit en expliquant comment déterminer l'ordre alpha de la réaction et la constante cinétique K grâce à une étude cinétique menée à différentes températures. Il souligne qu'en repérant l'unité de la constante de vitesse K (exprimée en secondes moins 1), on peut déduire que l'ordre alpha de la réaction est 1. Il propose ensuite une loi de vitesse qui relie la vitesse de la réaction à la concentration de N2O5. Ensuite, Mathis examine les données expérimentales fournies pour déterminer si elles sont compatibles avec la loi d'Arenius. Il explique comment effectuer une régression linéaire en utilisant la loi d'Arenius pour relier ln de K à 1 sur T. Les constantes obtenues dans la régression linéaire permettent de déterminer l'énergie d'activation et le facteur préexponentiel de la réaction. Les résultats obtenus sont une énergie d'activation de 15,0 kJ par mol et un facteur préexponentiel de 29,7 X 10³. En résumé, cette vidéo explique la loi d'Arenius concernant la décomposition du N2O5, détermine l'ordre alpha et la constante cinétique K, et effectue une régression linéaire pour obtenir des valeurs pour l'énergie d'activation et le facteur préexponentiel.