Cours de Mécanique en Ligne par les Meilleurs Professeurs - Mécanique

Moment cinétique d'un point de masse M

Dans cette vidéo, nous étudions le moment cinétique d'un point M se déplaçant en trajectoire circulaire autour d'un point O. Le point M possède une masse M et se déplace selon des coordonnées cylindriques. Le but de l'exercice est de calculer le moment cinétique Lz par rapport à l'axe OZ. Pour cela, nous commençons par faire un schéma de la situation, en représentant les vecteurs Uz, Ur et Uteta. Le point M se trouve à une distance R du centre O. Le moment cinétique d'un point M est le produit vectoriel de son vecteur position OM et de son vecteur vitesse MV. En substituant les valeurs, nous obtenons L = MR²θ.Uz. Cependant, nous cherchons le moment cinétique par rapport à l'axe OZ. En observant le schéma, nous remarquons que Uz et L sont tous les deux parallèles à OZ. Cela signifie que toutes les composantes du moment cinétique sont alignées avec OZ. Par conséquent, le produit scalaire entre L et Uz est égal à la norme de L. Ainsi, le moment cinétique par rapport à l'axe OZ du point M est égal à MR²θ.Uz. Ce résumé permet de poser les bases avant de passer à la suite du cours. Si vous avez des questions, n'hésitez pas à les poser. Merci.

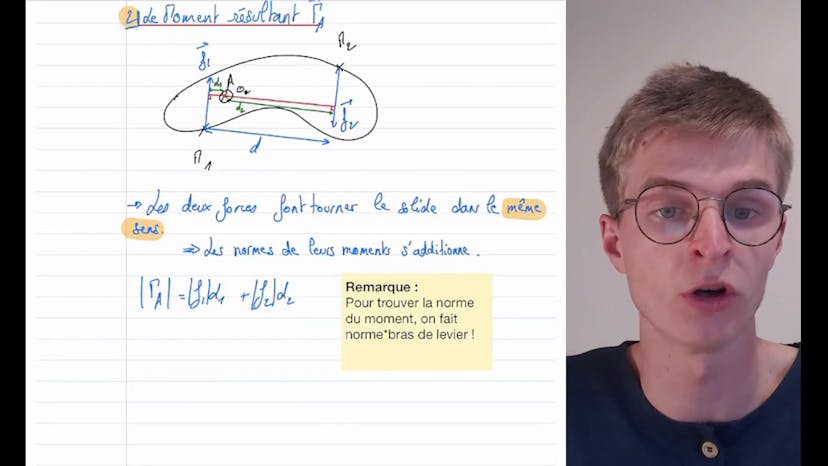
Couple de deux forces opposées

Dans cette vidéo, nous abordons le sujet des couples de forces appliquées à un solide indéformable. Un solide indéformable est soumis à deux forces opposées, F1 et F2, avec F1 étant inférieur à F2. F1 est appliquée au point M1 et F2 au point M2 du solide. Nous prenons un point A fixe sur le solide et calculons la force résultante F par rapport à A et le moment résultant gamma A par rapport à A. Pour calculer la force résultante F, nous effectuons un bilan des forces. Comme les forces F1 et F2 sont opposées, leur somme vectorielle donne 0. Par conséquent, la résultante par rapport à A est nulle. Le moment résultant gamma A est intéressant à examiner dans cet exercice. Les deux forces F1 et F2 contribuent à faire tourner le solide dans le même sens. Leurs moments respectifs s'additionnent, donnant gamma A égal à la norme du moment de F1 plus la norme du moment de F2. Pour calculer la norme d'un moment, il faut multiplier la norme de la force par le bras de levier correspondant. Par conséquent, gamma A est égal à F1 fois D plus F2 fois D, où D est la distance entre les points d'application des forces. Le moment résultant gamma A s'applique dans le plan orthogonal à OZ, dans lequel le solide est placé. Étant donné que le solide tourne dans le sens direct et que OZ rentre à l'intérieur de ce plan, le moment participe à faire tourner le solide dans le sens direct. Ainsi, le moment par rapport à A est égal à la norme de F1 fois D, avec une orientation selon UZ. Ce type de situation, où deux forces opposées avec la même norme contribuent à faire tourner le solide dans le même sens, est appelé un couple. Par conséquent, le couple dans cet exercice est représenté par F1 fois D fois UZ. C'est la fin de cet exercice. N'hésitez pas à poser des questions dans les commentaires et rejoignez-nous pour le prochain exercice.

Mouvement d'un pendule pesant

Dans cette vidéo, Théobald de Studio explique un exercice sur le pendule pesant. Le pendule est attaché au point O et oscille autour de l'axe OZ. On note J son moment d'inertie, G son centre de gravité, et D la distance OG. La première question demande de faire la liste des actions mécaniques appliquées sur le pendule et de calculer leur résultant et leur moment par rapport à l'axe OZ. Théobald explique que le poids du solide est P = -MGUY, car G et UY sont opposés. Le moment du poids est alors -MGDsinθUZ, car le poids tend à faire tourner le solide selon Uθ. En ce qui concerne la liaison pivot, son moment par rapport à l'axe Z est nul, et la force de la liaison pivot n'est pas encore déterminée. Ainsi, la force résultante est la somme du poids et de la force de la liaison pivot, et le moment résultant est -MGDsinθ. Dans la deuxième question, il est demandé d'appliquer le théorème du moment cinétique pour déterminer l'équation différentielle du mouvement. Théobald explique que le théorème du moment cinétique s'applique par rapport à un axe fixe OZ. La dérivée du moment cinétique par rapport au temps est égale au moment résultant. L'équation du mouvement s'obtient donc en substituant les valeurs connues : θ + MGDsinθ/J * sinθ = 0. La troisième question demande s'il est possible de retrouver cette équation en appliquant le théorème de la résultante cinétique. Théobald explique que le théorème de la résultante cinétique est essentiellement un PFD et fournit des informations sur les forces extérieures. Bien que l'on puisse obtenir des informations sur la force de la liaison pivot, il n'est pas possible de retrouver directement l'équation du mouvement en utilisant ce théorème. Cependant, en utilisant l'équation du mouvement, on peut déduire des informations sur la force de la liaison pivot, qui vaut MA-MG. Le cours se termine avec une invitation à poser des questions dans les commentaires et une promesse de nouvelles vidéos à venir.

Energie mécanique du pendule pesant

Dans cette vidéo, Théobald de Studio nous parle du pendule pesant et de son énergie mécanique. Il commence par décrire les différentes caractéristiques du pendule, telles que le moment d'inertie (J), le centre de gravité (G) et la distance entre G et l'axe des zéros (D). Il énonce ensuite les questions qui seront traitées dans l'exercice. La première question concerne l'énergie cinétique du pendule. Théobald explique que l'énergie cinétique d'un solide en rotation autour d'un axe fixe est égale à 1,5 de Jθ², où θ est l'angle de rotation du pendule. Ensuite, il aborde l'énergie potentielle du pendule. Il explique que cette énergie est égale à mgd(1-cosθ), où m est la masse du pendule, g est l'accélération due à la gravité, d est la distance entre G et l'axe des x, et θ est l'angle de rotation. Théobald explique alors pourquoi l'énergie mécanique du pendule est constante au cours du mouvement. Il explique que cela est dû au fait que les seules forces agissant sur le pendule sont le poids (une force conservative) et l'action de la liaison pivot (qui ne travaille pas). Par conséquent, l'énergie mécanique est une intégrale première du mouvement. La troisième question porte sur l'équation différentielle du mouvement du pendule. Théobald montre comment dériver l'expression de l'énergie mécanique par rapport à θ pour obtenir cette équation du mouvement. 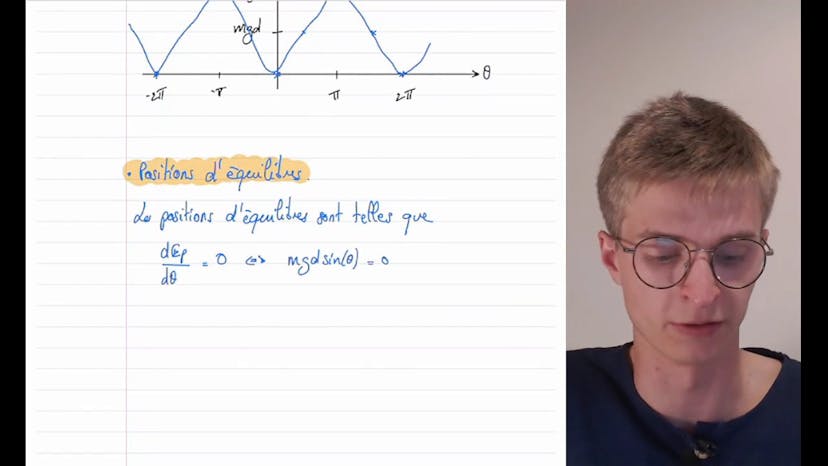Ensuite, il explique comment tracer le profil d'énergie potentielle du pendule et comment trouver les positions d'équilibre. Il montre que ces positions d'équilibre sont stables lorsque la dérivée de l'énergie potentielle par rapport à θ est positive, et instables lorsque cette dérivée est négative. Il discute ensuite des deux comportements possibles du pendule. Si l'énergie mécanique est inférieure à 2mgd, le pendule oscille entre deux positions extrêmes et a un comportement pendulaire. Si l'énergie mécanique est supérieure à 2mgd, le pendule peut prendre toutes les valeurs d'énergie potentielle et effectuer des tours complets, ce qui correspond à un comportement révolutif. En conclusion, Théobald souligne l'importance de bien comprendre tous les concepts abordés dans cet exercice, car ils sont récurrents et utiles dans le domaine du pendule pesant. Il encourage les spectateurs à poser des questions et annonce une prochaine vidéo à venir.

Saut de Tarzan

Dans cette vidéo, on étudie le mouvement de Tarzan se déplaçant le long d'une liane. Tarzan est assimilé à un point matériel de masse 70 kg. La liane est de longueur 10 mètres et de masse négligeable, accrochée à un point fixe O. Lorsqu'il attrape la liane, celle-ci forme un angle de 30 degrés avec la verticale. On néglige les frottements et la masse de la liane. La première question est de justifier l'utilisation des coordonnées polaires. Le mouvement s'effectue dans le plan vertical, car les forces appliquées sur Tarzan (son poids et la tension de la liane) sont verticales. De plus, le mouvement démarre avec une vitesse nulle, ce qui confirme que le mouvement se déroule dans le plan vertical. Étant donné que le mouvement est à la fois vertical et circulaire, on peut utiliser des coordonnées polaires. La deuxième question consiste à utiliser le théorème de l'énergie cinétique pour obtenir l'équation du mouvement. L'énergie cinétique du système est égale à 1/2 * masse * (longueur de la liane)^2 * (dérivée de l'angle theta par rapport au temps)^2. Les puissances des forces appliquées (poids et tension de la liane) sont calculées. En dérivant l'énergie cinétique par rapport au temps, on obtient l'équation du mouvement : (dérivée seconde de l'angle theta par rapport au temps) + (gravité * sinus de l'angle theta / longueur de la liane) = 0. La dernière question est de déterminer la tension s'exerçant sur Tarzan lorsque la liane forme un angle theta avec la verticale. On applique le principe fondamental de la dynamique : la masse fois l'accélération est égale à la somme des forces (poids et tension de la liane). En projetant cette équation sur le vecteur unitaire UR, on obtient une expression pour la tension en fonction de la masse, de la gravité, de l'angle theta et de l'angle alpha (angle lorsque Tarzan attrape la liane) : tension = 3 * masse * gravité * cos(theta) - 2 * masse * gravité * cos(alpha). Cet exercice est important pour comprendre le mouvement de Tarzan le long de la liane. La deuxième partie, où l'on cherche à déterminer la tension, est particulièrement significative. Si vous avez des questions, n'hésitez pas à les poser en commentaire.

Etude de manège

Dans cette vidéo, Oval2Studio aborde les questions suivantes concernant un manège : 1. Est-il possible de considérer un manège comme un solide indéformable ? 2. À quelles conditions les enfants peuvent-ils être inclus dans le modèle du solide indéformable ? 3. Un enfant peut-il être en translation circulaire sur un manège ? 4. Comment exprimer la vitesse d'un enfant assis sur un cheval sur le manège ? Un solide indéformable est un solide dont les points restent à une distance constante les uns des autres. Un manège vide peut être considéré comme un solide indéformable, mais la présence d'éléments mobiles tels que des chevaux peut rendre cette considération non valable. Pour inclure les enfants dans le modèle du solide indéformable, ils doivent être solidement attachés et complètement immobiles. Un enfant assis sur un manège n'est pas en translation circulaire car ses mains n'effectuent pas un mouvement circulaire avec le même rayon. Cependant, si l'enfant est assimilé à un point matériel, il est en translation circulaire. Pour calculer la vitesse de l'enfant, on le considère comme un point matériel situé à une distance de 2 mètres du centre du manège. La vitesse de rotation du manège est de 2π/24 radian par seconde. La vitesse de l'enfant est donc de 0,52 mètre par seconde. En conclusion, cet exercice démontre que la vitesse de l'enfant sur le manège dépend de sa position par rapport au centre du manège. Ce résumé SEO friendly couvre les principales questions et réponses de la vidéo d'Oval2Studio sur le manège.

Pendule à deux masses

Dans cette vidéo, nous étudions un pendule à deux masses. Le pendule est composé d'une tige rigide de longueur L, avec deux masses identiques de masse m fixées à une distance de L/2 et une distance L du centre O. Nous négligeons le moment d'inertie de la tige. Dans la première question, nous devons montrer que l'équation du mouvement s'écrit comme suit. Pour ce faire, nous utilisons le théorème du moment cinétique et appliquons la loi scalaire du moment cinétique par rapport à l'axe de rotation, donnant dLoz/dt = somme des moments des forces. Nous calculons les moments des forces exercées sur les masses (les poids P1 et P2) et obtenons l'équation du mouvement θ¨ + (6GM/5L)sinθ = 0. Dans la deuxième question, nous devons montrer que le centre de masse G du système se trouve à une distance de 3L/4 du centre O. En utilisant la définition du centre de masse, nous trouvons que OG = (3L/4)UR, confirmant que G est à une distance de 3L/4 de O. Dans la troisième question, nous devons déterminer si l'étude précédente est équivalente à celle d'un système où seule une masse de 2M est située en G. En appliquant la loi scalaire du moment cinétique à ce nouveau système, nous obtenons une équation du mouvement différente θ¨ + (4GM/3L)sinθ = 0. Par conséquent, les deux systèmes ne sont pas équivalents car ils ont des équations du mouvement différentes. Il est important de noter que la dynamique d'un solide en rotation n'est pas simplement donnée par la dynamique d'un point matériel en son centre d'inertie. Cette équivalence n'est valable que pour un solide en translation. Les deux systèmes étudiés dans cette vidéo sont donc distincts et donnent des équations du mouvement différentes.

Machine tournante et volant d'inertie

Dans cette vidéo, nous nous intéressons à une machine tournante équipée d'un volant d'inertie. Le volant d'inertie est un anneau de masse et de rayon ajouté à la machine tournante. Il permet de réguler la vitesse angulaire de rotation de la machine. On considère une machine tournante dont la vitesse angulaire de rotation est régulée par un volant d'inertie. Le volant d'inertie est un anneau lié au rotor, de masse élevée et de grand rayon. La machine tournante est modélisée par un moment d'inertie J et est soumise à un couple moteur constant γ0 et un couple de frottement fluide γf, égal à moins αω, où α est un certain coefficient positif. La première question demande de justifier, en utilisant un argument énergétique, que α est supérieur à 0. En regardant la puissance du couple de frottement, on constate qu'elle doit être négative. Pour que cela soit possible, α doit être positif dans l'équation. Donc, α est supérieur à 0. La deuxième question demande de trouver l'évolution de la vitesse angulaire ω en fonction du temps. On introduit la vitesse finale ωf et un temps caractéristique τ. En résolvant l'équation différentielle, on obtient que ω en fonction du temps est égal à ωf(1 - exp(-t/τ)). Ensuite, on introduit un couple de vibrations γvib égal à γcos(ωt) et on se demande pourquoi on ne perd pas en généralité en considérant ce couple. L'équation différentielle étant linéaire, on peut reconstruire la réponse à n'importe quelle forme de vibration grâce au théorème de Fourier. Ainsi, en ajoutant ce couple de vibrations, on rajoute simplement une contrainte supplémentaire au système, mais cela n'affecte pas la résolution de l'exercice. En considérant ce nouveau couple de vibrations, on cherche à déterminer le temps caractéristique de la durée du régime transitoire. Ce couple de vibrations ne dépend pas de ω et n'affecte pas le régime transitoire, qui est toujours caractérisé par τ, égal à J/α. Enfin, on cherche la vitesse angulaire de rotation après le régime transitoire, sous la forme ω = ωf + Acos(ωt + φ) et on nous demande de déterminer l'amplitude A. L'équation différentielle devient J(dω/dt) + γ0 - αω + γcos(ωt). En utilisant le principe de superposition, on trouve que A = γ/√(α² + Jω²). En conclusion, l'avantage d'un volant d'inertie est qu'il permet de stabiliser la vitesse angulaire d'une machine tournante en diminuant l'impact des variations et des vibrations. Cependant, son inconvénient est qu'il augmente la durée du régime transitoire, ce qui retardera l'atteinte du régime permanent.